Изучение диффузии примесей в структуре SiC/Si вызывает особый интерес, так как диффузия является одним из основных методов легирования полупроводников и полупроводниковых структур.
Структуры типа SiC/Si довольно перспективны в качестве материалов для экстремальной микроэлектроники в силу того, что карбид кремния обладает рядом преимуществ по сравнению со многими полупроводниковыми материалами: наличие широкой запрещенной зоны, механической и химической стойкости, хорошей теплопроводности, а также характерная высокая радио- и термостойкость дают возможность получения образцов как с электронной, так и дырочной проводимостью.
В реальных полупроводниках и полупроводниковых структурах диффузия примесей зачастую происходит при наличии неравномерного распределения структурных дефектов кристаллической решетки, полей упругих напряжений, контактных электрических полей, а также подвижных носителей заряда, что оказывает влияние на миграцию примесей в данных структурах.
Исследование диффузии позволяет выявить закономерности физических процессов, а также особенности их протекания при различных внешних условиях.
В качестве исследуемой структуры рассматривается пленка SiC, выращенная на p-Si (легирована бором B1). В такую структуру осуществляется диффузия бора B2 и фосфора P из постоянных источников с поверхности пленки. Одновременно идет процесс автолегирования пленки бором B1 из подложки. Весь процесс идет с учетом комплексообразования B-P+.
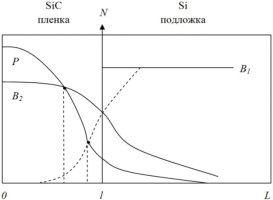
Рис. 1. Схематичное распределение бора и фосфора
Система дифференциальных уравнений, которая описывает данную задачу, запишется в следующем виде:
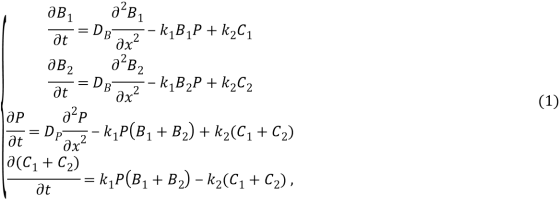
где 
— концентрация бора, диффундирующего из подложки, 
— концентрация бора, диффундирующего с поверхности пленки,
— концентрация фосфора, диффундирующего с поверхности пленки, 
— концентрация комплексов, образовавшихся при соединении примеси P c примесью 
, 
— концентрация комплексов, образовавшихся при соединении примеси P c примесью 
, 
— коэффициент диффузии бора, 
— коэффициент диффузии фосфора, 
— коэффициент комплексообразования, 
— коэффициент распада комплексов.
Первое уравнение системы (1) описывает диффузию бора B1 из подложки Si в пленку SiC, второе и третье — диффузию бора B2 и фосфора P с поверхности пленки в объем структуры, соответственно, и, наконец, последнее уравнение описывает диффузию комплексов. Предполагается при этом, что комплексы являются неподвижными, в данном случае коэффициент диффузии комплексов равен нулю.
Сложив первое и второе уравнение системы (1) имеем:
где 
, 
.
Начальные и граничные условия для концентраций примесей и комплексов имеют следующий вид:
В настоящее время существуют различные методы для численного решения дифференциальных уравнений типа (1) [1]. Наиболее универсальным является метод конечных разностей.
Данный метод основывается на введении разностной сетки в рассматриваемой области непрерывно изменяемого аргумента функции. Такая область заменяется совокупностью изолированных точек с фиксированным расстоянием между ними. Через значения функций в узлах сетки выражаются значения производных, начальные и граничные условия. В результате чего решение дифференциального уравнения сводится к решению системы алгебраических уравнений.
Для того чтобы решить систему уравнений (1) методом конечных разностей, введем относительные переменные. В нашем случае они упростят систему и будут являться приведенными концентрациями соответствующих примесей и их комплексов.
где 
, что соответствует уровню легирования подложки кремния бором.
Введем еще одну переменную
где 
, коэффициент диффузии бора в подложке.
Преобразуем систему (3) для дальнейшего решения уравнений:
Вернемся к системе (1) и с учетом (4) и (5) перепишем систему уравнений:
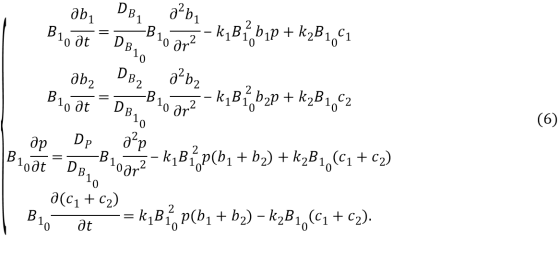
Пусть
Разделим теперь в системе (6) все на 
, учитывая условие (7):
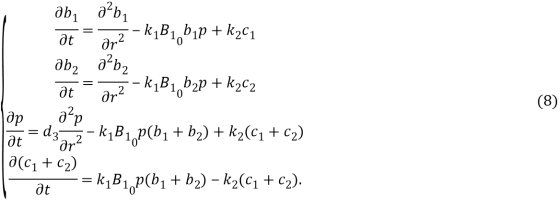
Составим теперь сеточную функцию для решения системы (1), тогда первая производная будет иметь вид:
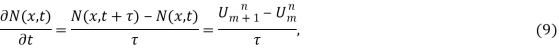
а вторая выглядит следующим образом:
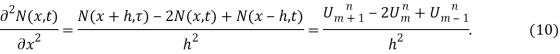
Произведем в первом уравнении системы (8) замену (9) и (10):
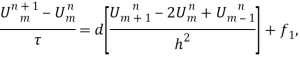
где 
.
Таким образом, разностная схема для первого уравнения будет представлена в таком виде:
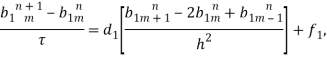
преобразуя, получаем:
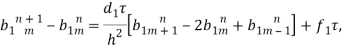
Остальные уравнения системы (8) представим аналогичным образом:
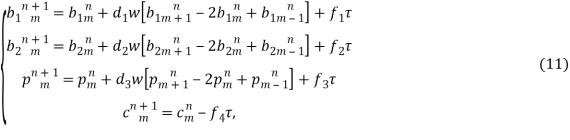
где 
— шаг по времени, 
— шаг по координате.
Таким образом, в результате последовательных преобразований уравнений системы (1) методом конечных разностей получили более простые уравнения.
Начальные и граничные условия в таком случае имеют следующий вид:
Основываясь на приведенном нами выше алгоритме решения нелинейных дифференциальных уравнений для вычисления распределения примесей, составляется блок-схема для разработки программы на языке программирования Pascal.
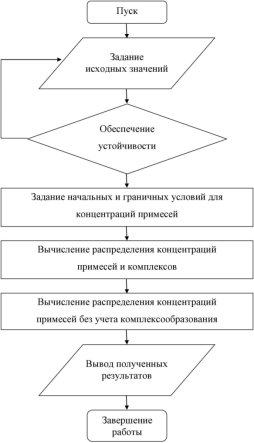
Рис. 2. Блок-схема программы
Решение задачи одновременной диффузии двух заряженных примесей в структуре SiC/Si состоит в рассмотрении трех областей: пленки, подложки и линии границы «пленка-подложка», в которых содержатся распределения концентраций B1, B2, (B1+B2), P и суммарного распределения комплексов (С1+С2) на отдельном слое по времени, цикл повторяется снова до тех пор, пока все слои разностной сетки не будут просчитаны по времени и по координате [2; 3].
Программа позволяет провести расчет распределения концентраций примесей B1, B2, (B1+B2), P и суммарного распределения комплексов (С1+С2) по глубине структуры подложка Si-пленка SiC при различных технологических параметрах: от времени и температуры диффузионного отжига, коэффициентов образования и распада комплексов, вводимых концентрации примесей с пленки, а также от уровня легирования подложки.
Литература:
- Самарский А. А., Гулин А. В. Численные методы математической физики. — 2-е изд. — М.: Научный мир, 2003. — 316 с.
- Malkovich R. Sh., Pokoeva V. A. Impurity Diffusion with Complex Formation. // phys. stat. sol. (b), 1977, 82, p. 421–428.
- Pokoeva V. A. Ionized Impurity Diffusion in a Semiconductor. // phys. stat. sol. (b), 1992, 169, k1.
