Амортизаторы являются элементами активной безопасности автомобиля. Они должны обеспечивать безопасность и комфортабельность движения путем улучшения стабильности контакта шин с дорогой и снижения резонансных колебаний кузова и колес. В технической литературе, посвященной теории подрессоривания автомобилей, уделяется мало внимания динамике деформации шин. Однако именно деформации шин определяют стабильность контакта протектора шин с дорогой, от которой существенно зависят управляемость, курсовая устойчивость и тормозные свойства, влияющие на безопасность движения автомобиля. Рассмотрим зависимость деформации шины от характеристик амортизатора, жесткости шины и подвески.
Автомобильная подвеска удовлетворительно моделируется одноопорной двухмассовой колебательной системой (рис. 1).
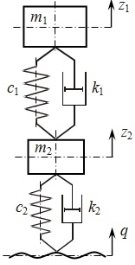
Рис. 1. Расчетная схема автомобильной подвески: m1 — подрессоренная масса; m2 — неподрессоренная масса; с1 — жёсткость рессоры; с2 — жёсткость шины; k1 — коэффициент демпфирования подвески; k2 — коэффициент демпфирования шины; z1 — перемещение подрессоренной массы; z2 — перемещение неподрессоренной массы; q — кинематическое возмущение колебаний
В соответствии с расчётной схемой уравнения динамики системы имеют следующий вид:
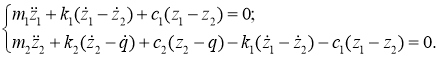(1)
Преобразовав уравнение (1), получим:
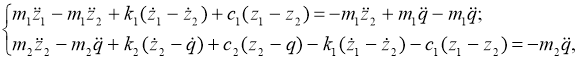(2)
Для получения закона деформации шины введем следующие обозначения: 
— деформация подвески, 
— деформация шины.
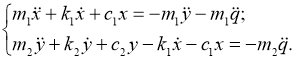(3)
Разделим первое и второе уравнения на m
и m
соответственно и используем обозначения: 
— относительная масса; 
— удвоенное значение парциального относительного коэффициента демпфирования подвески; 
— удвоенное значение парциального относительного коэффициента демпфирования шины; 
— квадрат парциальной собственной частоты колебаний подрессоренной массы; 
— квадрат парциальной собственной частоты колебаний неподрессоренной массы:
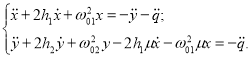(4)
Решение этой системы уравнений относительно переменной y для синусоидального профиля можно представить в виде коэффициента динамичности:
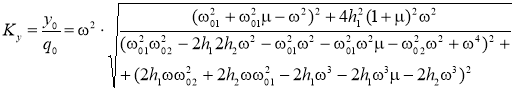. (5)
Здесь 
— амплитуда деформаций шины.
По выражению (5) можно построить графики амплитудно-частотных характеристик деформаций шин.
Рассмотрим последнее выражение для коэффициента динамичности деформаций шин. Поскольку демпфирование в шине мало и не оказывает существенного влияния на процесс колебаний, примем допущение: 
. Получим:
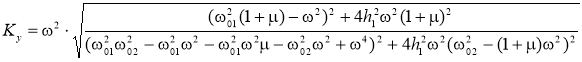(6)
Условие безотрывного движения: 
, где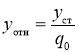 
(
— статическая деформация шины). Тогда из формулы (6) получим:
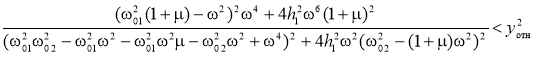,(7)
Для получения значений парциального относительного коэффициента демпфирования подрессоренной массы, удовлетворяющих условию безотрывного качения шины, решим это неравенство относительно 
. Получим следующие условия безотрывного качения колеса:
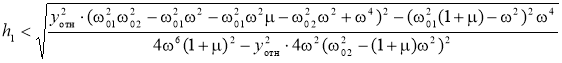(8)
при 
,
и 
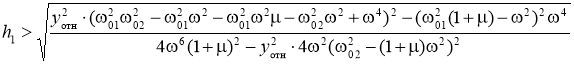(9)
при 
.
;
;
.
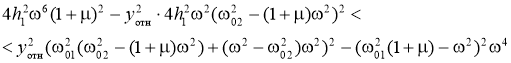
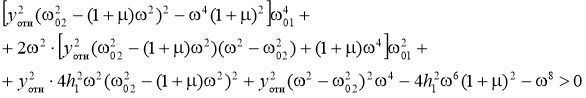
На рис. 2 представлены амплитудно-частотные характеристики амплитуд перемещений подрессоренной массы, неподрессоренной массы, деформаций подвески и деформаций шин для колебательной системы с 
, 
, 
, 
, 
. Горизонтальной пунктирной линией обозначена величина, соответствующая величине относительной статической деформации шины 
.
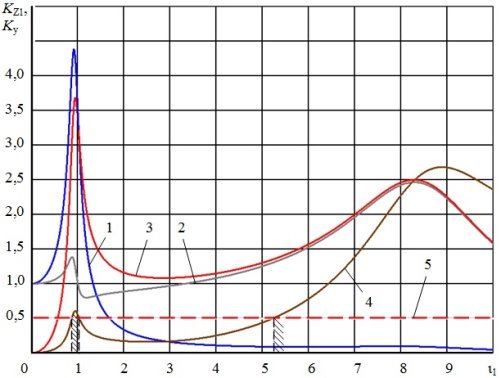
Рис. 2. Амплитудно-частотные характеристики амплитуд перемещений подрессоренной массы (1), неподрессоренной массы (2), деформаций подвески (3) и деформаций шин (4) для колебательной системы с
, , , . Линия (5) соответствует величине относительной статической деформации шины . Заштрихованные зоны соответствуют частотам, при которых динамические деформации шин превышают статическую (происходит отрыв шин)
На рис. 3 представлены результаты проведенного исследования для колебательной системы с , , , , в виде зависимости граничных значений парциального относительного коэффициента затухания колебаний подрессоренной массы от частоты возмущения 
. Заштрихованные области соответствуют условиям отрыва шины от опорной поверхности.
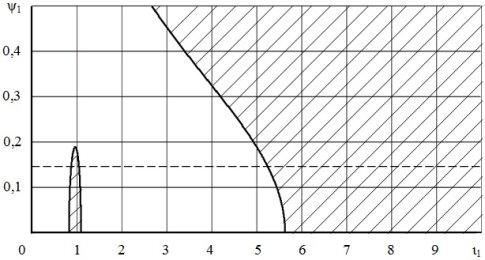
Рис. 3. Зависимость граничных значений парциального относительного коэффициента затухания колебаний подрессоренной массы от частоты возмущения, определяющая условия безотрывного движения и отрыва шины от опорной поверхности для колебательной системы с , , , : заштрихованные области соответствуют условиям отрыва шины от опорной поверхности; пунктирная линия соответствует 
Анализ рис. 3 показывает, что при заданном уровне демпфирования и статической деформации шины в низкочастотной области колебаний имеется узкий диапазон частот, в котором возникают условия отрыва шины от опорной поверхности (между точками пересечения кривой, огибающей заштрихованную зону, и пунктирной прямой). В высокочастотной области колебаний отрывы шин начинаются на частоте, соответствующей точке пересечения пунктирной прямой с кривой, ограничивающей заштрихованную область, причем высокочастотный диапазон не имеет правой границы, т. е. отрывы шин автомобиля от опорной поверхности будут возникать при любых частотах возмущения, находящихся правее указанной характерной точки.
Таким образом, оптимизируя параметры автомобильной подвески возможно уменьшение деформации шины и достижение безотрывного перемещения колеса по дороге и бездорожью. Так же уменьшая данные показатели, мы увеличиваем характеристики транспортного средства, такие как управляемость, курсовая устойчивость и тормозные свойства.
Литература:
- Повышение безопасности автомобиля за счет рационального выбора шин с учётом характеристик амортизаторов / И. М. Рябов, К. В. Чернышов, М. М. Газанов, Ш. М. Мухучев // Известия ВолгГТУ. Сер. Наземные транспортные системы. Вып. 10: межвуз. сб. науч. ст. / ВолгГТУ. — Волгоград, 2015. — № 4 (162). — C. 45–49.
- Рябов И. М. Выбор высоты профиля шин автомобиля с учетом технического состояния амортизаторов / И. М. Рябов, К. В. Чернышов, А. В. Поздеев, В. Д. Гудков, Ш. М. Мухучев, Ю. М. Мухидинов // Шина плюс: всеукраинский журнал. — 2016. — № 5. С. 8–10.
