В статье на основе применения различных моделей турбулентного пограничного слоя получены выражения для вычисления коэффициентов переноса импульса и теплоты. Для определения параметров полученных уравнений в пограничном слое с различными возмущениями (кривизна, шероховатость поверхности и т.д.) использовались известные свойства консервативности законов пограничного слоя (подход Кутателадзе, Леонтьева и т.д.) и балансовые соотношения переноса импульса.
Проблема математического описания процессов турбулентного переноса тепла в одно- и двухфазных средах является одной из важных фундаментальных проблем современной науки. Повышенный интерес к проблеме математического описания процессов переноса в турбулентном пограничном слое определяется не только теоретической значимостью, но и значительными прикладными аспектами, в том числе для проектирования и интенсификации работы теплообменных аппаратов в различных отраслях промышленности.
Ввиду крайне сложного характера физических процессов, сопровождающих турбулентный перенос, существующие в настоящее время теоретические подходы к решению такого рода задач являются полуэмпирическими. Теоретическая возможность прямого численного моделирования «упирается» в низкую производительность существующих ЭВМ и не представляется возможной в обозримом будущем.
Помимо методов расчета пограничного слоя, основанных на теории Буссинеска (называемых также полными по классификации, предложенной в [1]) в инженерно-научной практике исследования тепломассообменного оборудования широкое распространение получили интегральные и интегрально-параметрические методы расчета турбулентного пограничного слоя. Несомненным удобством последних, помимо очевидной простоты, является удобство встраивания в алгоритмы системного анализа промышленных процессов, не требующее отвлечения значительных вычислительных ресурсов и высокой квалификации инженерного персонала. Очевидным недостатком семейства интегральных методов расчета турбулентного пограничного слоя является то, что получаемые эмпирические и полуэмпирические уравнения обладают малой областью применения и фактически описывают лишь один из частных случаев.
Очевидно, что семейство интегральных моделей переноса в турбулентном пограничном слое является эмпирически найденной наилучшей формой аппроксимации решения полных, дифференциальных, моделей, связывающее характерные величины процессов в пограничном слое с характерными величинами внешнего потока. Таким образом, при функциональном моделировании промышленных процессов и аппаратов интегральные модели могут быть применены как в ходе решения самих систем дифференциальных уравнений так и в ходе математического взаимодействия функционального блока системы пограничного слоя с системами более высокого порядка [2].
Сложившийся же разрыв между дифференциальными и интегральными методами расчета вызван в основном недостаточным использованием методов функционального и системного моделирования в научно-инженерной практике.
В данной работе приведены новые соотношения позволяющие, использовать преимущества как интегральных так и дифференциальных моделей.
Так называемые полные полуэмпирические модели турбулентности, в основной своей массе, основаны на двух основных направлениях развития гипотезы Буссинеска: Прандтля-Кармана и Колмогорова. Стремительное увеличение производительности процессоров в последние десятилетия послужило толчком к развитию моделей турбулентного переноса моментов порядка второго и выше, основанных на гипотезе Колмогорова. Однако, как отмечено в работах [3], существенное усложнение вычислительных алгоритмов, сопровождающее использование таких моделей, зачастую не сопровождается увеличением точности вычислений по сравнению с моделями на основе моментов первого порядка, так называемых алгебраических. Во многом это связано со свойствами консервативности гидродинамического пограничного слоя, выражающимися в частности как:
консервативность длины пути смешения в окрестности стенки (но вне вязкого подслоя) относительно градиента давления и сжимаемости;
вырождение вязкого подслоя и пульсаций плотности при Re→∞ и, как следствие этого, существование предельных относительных законов трения, в общем виде не зависящих от интегральных констант турбулентности;
значительная консервативность безразмерной толщины вязкого подслоя на непроницаемой поверхности.
В рамках решения задач переноса в пограничном слое, вполне можно ограничиться алгебраическими моделями турбулентной вязкости в том числе и при сложных гидродинамических условиях.
С другой стороны в ходе многочисленных экспериментов была установлена существенная консервативность теплового и диффузионного пограничных слоев по сравнению с гидродинамическим. Во многом этим (хотя и не только) объясняется нарушение гидродинамической аналогии для течений в сложных геометрических условиях. На рисунке 1 хорошо видно, что сравнительно небольшие изменения продольного градиента давления, как в положительную, так и в отрицательную сторону, слабо влияют на распределение относительной температуры по высоте пограничного слоя. И, напротив, распределение безразмерной продольной скорости, как показано на рисунке 2 довольно сильно зависит от изменения давления.
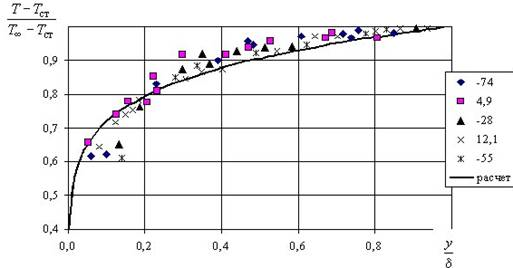
Рис. 1. Влияние продольного градиента давления на распределение температуры по сечению пограничного слоя [4]: кривая – расчет по формуле 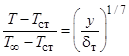 .
.
|
|
-74 |
-55 |
-28 |
4,9 |
12,1 |
|
Обозначение |
|
|
|
|
|
Обозначено: 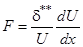 - формпараметр градиентного течения;
- формпараметр градиентного течения; 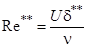 - число Рейнольдса, вычисляемое по толщине потери импульса
- число Рейнольдса, вычисляемое по толщине потери импульса 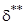 ; T – текущая температура по высоте пограничного слоя;
; T – текущая температура по высоте пограничного слоя; 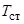 - температура на стенке;
- температура на стенке; 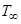 - температура в ядре потока;
- температура в ядре потока; 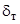 - толщина теплового пограничного слоя.
- толщина теплового пограничного слоя.
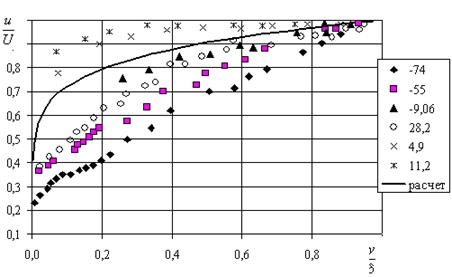
Рис. 2. Влияние продольного градиента давления на распределение скоростей по сечению пограничного слоя [4] кривая – расчет по формуле 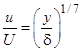 .
.
|
|
-74 |
-55 |
-9,06 |
4,9 |
11,2 |
4,9 |
28,2 |
|
Обозначение |
|
|
|
|
|
|
|
Здесь u – текущая средняя скорость по высоте пограничного слоя; U - скорость в ядре потока; 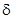 - толщина гидродинамического пограничного слоя.
- толщина гидродинамического пограничного слоя.
На основании вышесказанного возможно моделирование тепломассоотдачи в пограничном слое на основе гидродинамической аналогии не только в случае простых (канонических) течений, но и для течений, осложненных различными возмущающими факторами. В этом случае характеристики гидродинамического пограничного слоя рассчитываются также как и для невозмущенного течения, а учет возмущающих факторов учитывается с помощью эффективных (эквивалентных величин). Принципы подбора эквивалентных величин были сформулированы авторами [5]. В качестве таковых могут быть выбраны любые интегральные гидродинамические характеристики пограничного слоя, в совокупности достаточные для описания величины диссипации механической энергии в пограничном слое.
В рамках данной работы в качестве эффективных величин используются динамическая скорость - 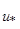 , максимальная разность скоростей по высоте пограничного слоя
, максимальная разность скоростей по высоте пограничного слоя 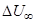 ,
, 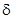 - толщина пограничного слоя. В качестве эффективной, как правило, принимается толщина пограничного слоя -
- толщина пограничного слоя. В качестве эффективной, как правило, принимается толщина пограничного слоя - 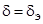 . Остальные величины находятся из гидродинамических условий осложненного течения.
. Остальные величины находятся из гидродинамических условий осложненного течения.
Для математической связи этих характеристик пограничного слоя используются следующие соотношения баланса импульса и диссипации энергии:
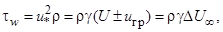
Здесь 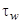 -касательное напряжение на стенке, Н/м2;
-касательное напряжение на стенке, Н/м2; 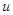 - осредненная скорость по потоку, м/с;
- осредненная скорость по потоку, м/с; 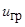
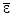 - среднеобъемная диссипация энергии в пограничном слое, Вт/м3;
- среднеобъемная диссипация энергии в пограничном слое, Вт/м3; 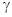 - коэффициент переноса импульса, м/с [2; 6].
- коэффициент переноса импульса, м/с [2; 6].
Коэффициент переноса импульса может быть найден из следующего уравнения:
где 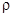 -плотность среды, кг/м3;
-плотность среды, кг/м3; 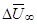 -максимальная разность скоростей по высоте пограничного слоя, м/с;
-максимальная разность скоростей по высоте пограничного слоя, м/с; 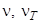 - молекулярный и турбулентный коэффициенты кинематической вязкости соответственно, м2/с.
- молекулярный и турбулентный коэффициенты кинематической вязкости соответственно, м2/с.
В , очевидно, делается допущение о слабом относительном изменении касательного напряжения 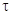 по высоте пограничного слоя:
по высоте пограничного слоя: 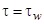 . Оно вполне правомерно для пристенной подобласти пограничного слоя, где сосредоточено основное сопротивление переносу, и подтверждено многочисленными сравнениями с экспериментальными данными [2; 6-7].
. Оно вполне правомерно для пристенной подобласти пограничного слоя, где сосредоточено основное сопротивление переносу, и подтверждено многочисленными сравнениями с экспериментальными данными [2; 6-7].
Вид функции коэффициента переноса импульса в определяется видом исходных функций турбулентной вязкости 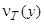 .
.
Выражения для некоторых функций коэффициента переноса импульса показаны в табл. 1.
Таблица 1 Выражения для коэффициентов переноса импульса в зависимости от исходной функции турбулентной вязкости
|
№
|
Вид исходной зависимости коэффициента турбулентной кинематической вязкости |
Источник |
Коэффициент переноса импульса |
Источник |
|
1 |
|
[8] |
|
Данные автора |
|
2 |
|
[9] |
|
[6] |
|
3 |
|
[10] |
|
Данные автора |
|
4 |
где |
[7] |
|
[11] |
Обозначения в табл. 1: 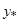 =
= 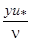 - безразмерная координата по высоте пограничного слоя,
- безразмерная координата по высоте пограничного слоя, 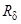 =
= 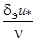 - безразмерная эффективная высота пограничного слоя;
- безразмерная эффективная высота пограничного слоя; 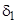 - граница вязкого подслоя турбулентного пограничного слоя, м;
- граница вязкого подслоя турбулентного пограничного слоя, м; 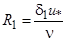 - безразмерная граница вязкого подслоя турбулентного пограничного слоя;
- безразмерная граница вязкого подслоя турбулентного пограничного слоя; 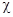 - коэффициент Прандтля.
- коэффициент Прандтля.
Коэффициент переноса тепла на основании вышеописанных положений вычисляется исходя из интегрального выражения гидродинамической аналогии:
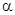 - коэффициент теплоотдачи, Дж/(м2 ∙с),
- коэффициент теплоотдачи, Дж/(м2 ∙с), 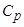 - теплоемкость среды, Дж/(кг∙К);
- теплоемкость среды, Дж/(кг∙К); 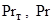 - турбулентное и молекулярное число Прандтля соответственно.
- турбулентное и молекулярное число Прандтля соответственно.
Также в упрощенном виде может использоваться выражение гидродинамической аналогии в форме:
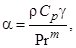
В качестве примера рассмотрим случай поперечного обтекание коридорного пучка труб.
В [6] было получено выражение для коэффициента турбулентной вязкости в рамках вязкого подслоя:
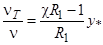 .
.
Используя двухслойную модель турбулентного пограничного слоя (Прандтля) из получено:
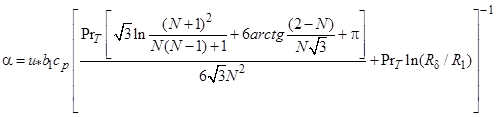 .
.
 ;
; 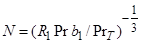 ; где χ и R1-характеристики пограничного слоя; R1=11,6; χ=0,4;
; где χ и R1-характеристики пограничного слоя; R1=11,6; χ=0,4; 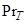 -турбулентное число Прандтля,
-турбулентное число Прандтля, 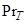 »1.
»1.
Средняя движущая сила переноса импульса, м/с:
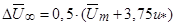
где 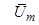 - средняя скорость в узком сечении пучка, м/с;
- средняя скорость в узком сечении пучка, м/с;
Влияние формы обтекаемых пучков учитывается с помощью полученного на основе в [12] выражения динамической скорости:
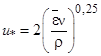 . (10)
. (10)
Среднюю диссипацию энергии 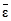 в объеме пучка труб V представим через перепад давления ∆P:
в объеме пучка труб V представим через перепад давления ∆P:
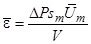 (11)
(11)
где 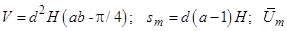 - средняя скорость в узком сечении пучка, м/с; a b – относительный поперечный и продольный шаг пучка соответственно, a=s1/d; b=s2/d; d-диаметр трубок, м; Н-длина труб, м.
- средняя скорость в узком сечении пучка, м/с; a b – относительный поперечный и продольный шаг пучка соответственно, a=s1/d; b=s2/d; d-диаметр трубок, м; Н-длина труб, м.
Перепад давления ∆P, обусловленный сопротивлением трения и формы трубок, определяется по выражению [13]:
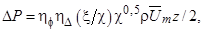 (12)
(12)
где  коэффициент, учитывающий угол атаки φ пучка труб
коэффициент, учитывающий угол атаки φ пучка труб 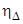 , при φ=90
, при φ=90 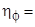 1;
1; 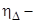 коэффициент, учитывающий шероховатость (рассматриваются абсолютно гладкие трубы
коэффициент, учитывающий шероховатость (рассматриваются абсолютно гладкие трубы 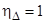 ); χ-формпараметр, зависящий от a и b; отношение (ξ/χ) определяется по номограммам [13]; χ - по вспомогательному графику, в зависимости от комплекса
); χ-формпараметр, зависящий от a и b; отношение (ξ/χ) определяется по номограммам [13]; χ - по вспомогательному графику, в зависимости от комплекса 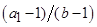 ; z-количество рядов.
; z-количество рядов.
Эффективная толщина пограничного слоя может быть вычислена по любому из уравнений в табл. 1.
Выполнен расчет коэффициентов теплоотдачи по выражениям (2) и (3) при поперечном движении однофазного потока в коридорных пучках труб (2×103 ≥ Re ≥ 2×105).
Результаты расчета коэффициента α и опытные данные [14] представлены на рис.3:
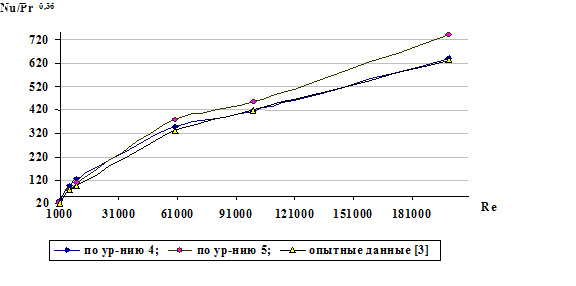
На основании полученных результатов можно сделать вывод о том, что расчеты по уравнениям (6) и (8), удовлетворительно согласуется с известными экспериментальными данными.
Расхождение результатов составляет около 10-15%, что подтверждает справедливость использования обобщенной гидродинамической аналогии.
Список использованной литературы
1. Патанкар С.В., Сполдинг Д.Б. Тепло- и массообмен в пограничных слоях / пер. Лыков А.В. - М.: Энергия, 1971.
2. Дьяконов С.Г., Елизаров В.И., Лаптев А.Г. Теоретические основы и моделирование процессов разделения веществ. - Казань: Изд-во Казанского университета, 1993.
3. Лапин Ю.В. Статистическая теория турбулентности (прошлое и настоящее – краткий очерк идей) // Научно технические ведомости. 2004. 2.
4. Кутателадзе С.С., Леонтьев А.И. Тепломассообмен и трение в турбулентном пограничном cлое - 2-е изд., перераб. - М.: Энергоатомиздат, 1985.
5. Лаптев А.Г., Дьяконов С.Г., Елизаров В.И. Математическое моделирование теплоотдачи при турбулентном обтекании пучков труб // Теплоэнергетика. 1992. № 12. с. 34-38.
6. Лаптев А.Г. Модели пограничного слоя и расчет тепломассообменных процессов. - Казань: Изд-во Казанск. гос. ун-та, 2007.
7. Шлихтинг Г. Теория пограничного слоя / пер. Вольперта Г.А.; под. ред. Лойцянского Л.Г. - М.: Главная редакция физико-математической литературы издательства «Наука» 1974.
8. Кадер Б.А. К строению вязкого подслоя турбулентного пограничного слоя несжимаемой жидксости // Изв. АН СССр Мех. жидк. и газа. 1966. №6. стр. 157-163.
9. Clauser F.H. The turbulent boundary layer. Advances in applied mechanics / Clauser F.H. - New York: Academic Press, Inc. , 1956: Vol. 4 - p. 2-51.
10. Лойцянский Л.Г. Механика жидкости и газа: Учеб. пособие для вузов. – 7-е изд., испр. . - М.: Дрофа, 2003.
11. Энергоресурсосберегающие модернизации установок разделения и очистки газов и жидкостей на предприятиях нефтегазохимического комплексадис: д-ра техн. наук / Фарахов М.И. - Казань: КГТУ, 2009.
12. Соколов В.Н., Доманский И.В. Газожидкостные реакторы. - Л.: Машиностроение (Ленинградское отд-ние), 1976.
13. Жукаускас А.А. Конвективный переноса в теплообменниках. - М.: Наука, 1982.
14. Жукаускас А., Макарявичюс В., Шланчяускас А Теплоотдача пучков труб в поперечном потоке жидкости. - Вильнюс: «Минтис» 1968.
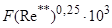



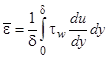 .
. 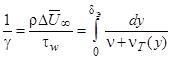 ,
, 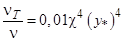 ,
, 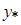 <5 ;
<5 ;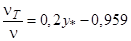 , 5<
, 5<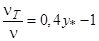 при
при 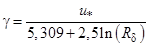 .
.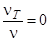 , 0<
, 0<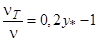 , 5<
, 5<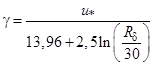 .
.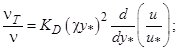
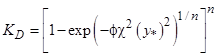 ; где n = 2,
; где n = 2, 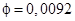
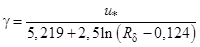 .
.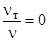 , 0<
, 0<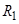 ;
;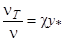 ,
, 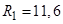
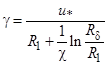 .
.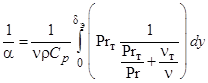 ,
, 
