Библиографическое описание:
Жураев, Ф. М. Об одной краевой задаче для нагруженного уравнения параболо-гиперболического типа, вырождающегося внутри области / Ф. М. Жураев. — Текст : непосредственный // Молодой ученый. — 2017. — № 25 (159). — С. 6-8. — URL: https://moluch.ru/archive/159/43928/ (дата обращения: 26.04.2024).
Краевые задачи для невырождающихся нагруженных уравнений смешанного типа второго и третьего порядка, когда нагруженная часть содержит след или производную от искомой функции, изучены в работах А. М. Нахушева [1], Б.Исломова и Д. М. Курьязова [2], Б.Исломова и У. И. Болтаевой [3].
Несколько нам известно, краевые задачи типа задачи Трикоми и Геллерстедта для вырождающегося нагруженного уравнения смешанного типа второго порядка исследовались сравнительно мало. Отметим работы В. М. Казиева [4], Б.Исломова и Ф.Джураева [5]. Исходя из этого, настоящая работа посвящена постановке и исследованию краевой задачи типа задачи Геллерстедта, для нагруженного уравнения параболо-гиперболического типа, вырождающегося внутри области.
Рассмотрим уравнение
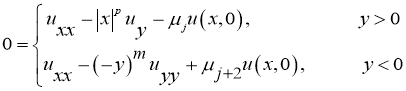
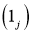
где 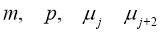 - любые действительные числа, причем
- любые действительные числа, причем
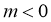 ,
, 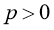 ,
, 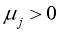 ,
, 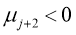
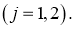
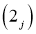
Здесь и делее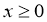 при
при 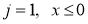 при
при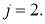
Пусть D–конечная односвязная область плоскости переменных 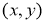 , ограниченнаяпри
, ограниченнаяпри 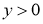 отрезками
отрезками 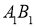 ,
, 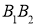 ,
, 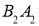 ,
, 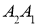 прямых
прямых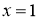 ,
,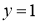 ,
,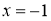 ,
,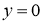 соответственно, a при
соответственно, a при 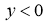 характеристиками
характеристиками
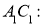
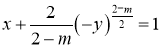 ,
, 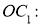
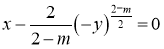 ,
,
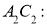
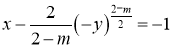 ,
, 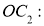
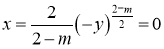
уравнения
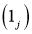
, выходящими из точек
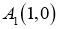
,
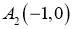
,
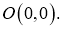
Из произвольных точек 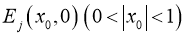 проведем характеристиками
проведем характеристиками
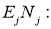
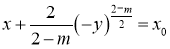 ,
, 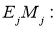
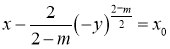
уравнения 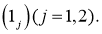
Введем следующие обозначения: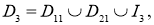
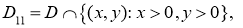
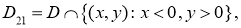
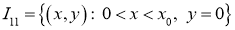 ,
, 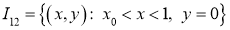 ,
,
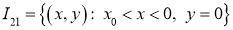 ,
, 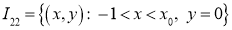 ,
,
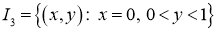 ,
, 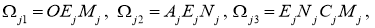
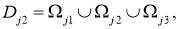
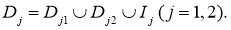
В области 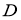 для уравнения
для уравнения 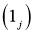 исследуем следующую задачу:
исследуем следующую задачу:
Задачи G. Требуется найти функцию
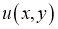
, обладающую следующими свойствами:
1) 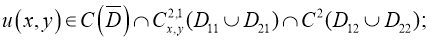
2)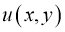 является регулярным решением уравнения
является регулярным решением уравнения 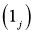 в областях
в областях
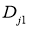 и
и 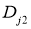
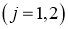 ;
;
3) 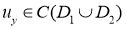 причем
причем 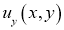 может обращаться бесконечность порядок
может обращаться бесконечность порядок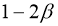 при
при 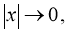 и
и 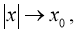 а при
а при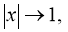 ограничена;
ограничена;
4)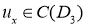 на линии вырождения
на линии вырождения 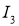 выполняется условия склеивания
выполняется условия склеивания
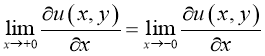 ,
, 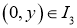
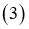
5)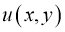 удовлетворяет краевым условиям
удовлетворяет краевым условиям
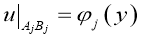 ,
, 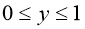 ,
, 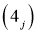
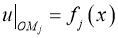 ,
, 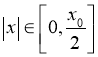 ,
, 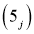
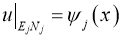 ,
, 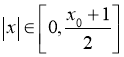 ;
; 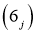
где
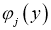
,
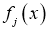
,
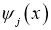
,
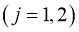
- заданные функции, причем
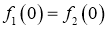
,
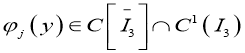 ,
, 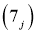
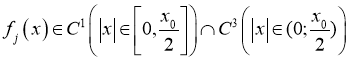 ,
, 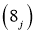
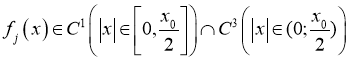 ,
,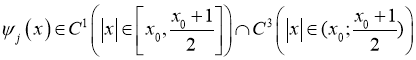 ,
, 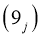
Здесь 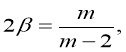 причем
причем
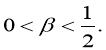
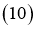
Доказана следующая теорема.
Теорема. Если выполнены условия 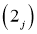 ,
, 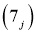 ,
, 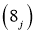 ,
, 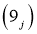 ,
,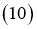 то в области
то в области 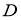 решение задачи G существует и единственно.
решение задачи G существует и единственно.
Литература:
-
Нахушев А. М. Нагруженные уравнения и их приложения. //«Дифференциальные уравнения». 1983. Т.19. № 1. С. 86–94.
-
Исломов Б., Курьязов Д. М. Краевые задачи для смешанного нагруженного уравнения третьего порядка параболо-гиперболического типа. // «Узбекский математический журнал». 2000. № 2. С. 29–35.
-
Б.Исломов Б., Болтаева У. И. Краевая задача для нагруженного уравнения третьего порядка с параболо-гиперболическим оператором. // «Узбекский математический журнал». 2007. № 2. С. 45–55.
-
Казиев В. М. О задаче Дарбу для одного вырождающегося нагруженного интегро-дифференциального уравнения второго порядка. //«Дифференциальные уравнения». 1978. Т.14. № 1. С.181–184.
-
Исломов Б., Джураев Ф. Аналог задачи Трикоми для вырождающегося нагруженного уравнения параболо-гиперболического типа. // «Узбекский математический журнал». 2011. № 2. С. 75–85.
Основные термины (генерируются автоматически): краевая задача типа задачи, уравнение.
Похожие статьи
В прямоугольной области изучается краевая задача для модельного уравнения второго порядка. (1). Где. И , И , . Пусть , , вектор внутренней нормали к границе области , . Заметим, что уравнение (1) в области является уравнением смешанного типа.
В этой статье рассматривается краевая задача для уравнения смешанного типа и приводится лемма для решения задачи, которая далее используется для доказательства устойчивости разностной модели, построенной для этой краевой задачи.
Для уравнения (1) изучаем следующую краевую задачу: Краевая задача: Найти функцию , удовлетворяющую в области уравнения (1), а при
Алоев Р. Д., Рахмонов Х. О., Шарипова Ш. Исследование разностной модели краевой задачи для уравнения смешанного типа.
В данной работе рассматривается проблема решения краевых задач для уравнений эллиптического типа. Эти задачи являются стационарными, так как в них отсутствует временная переменная.
Автоматизация решения задач данного типа во много раз ускорит учебный процесс и позволит студентам приобрести навыки математического и компьютерного моделирования различных физических процессов.
Решается первая начально-краевая задача для волнового уравнения.
Для дифференциальных уравнений различают три типа задач: задача Коши; краевая задача; смешанная задача.
Решения задачи Коши задается формулой Даламбера: . (4). В полуограниченной области для уравнение (2) мы можем ставить следующие краевые задачи...
Ключевые слова: краевая задача, линейный оператор, функционально-дифференциальное уравнение.
Аппроксимация первой краевой задачи разностной моделью для уравнения смешанного типа.
Задача Геллерстедта для общих линейных систем уравнений смешанного типа рассматривалась лишь в работе [6]. В ней рассматривается система вида.
Априорная оценка для решения первой краевой задачи для уравнения смешанного типа.
Библиографическое описание: Комилова Х. М. Задача Трикоми для уравнения параболо-гиперболического типа с нелокальными условиями склеивания
Отметим, что краевые задачи с нелокальными условиями склеивания для параболо-гиперболических уравнений известны в...
В прямоугольной области изучается краевая задача для модельного уравнения второго порядка. (1). Где. И , И , . Пусть , , вектор внутренней нормали к границе области , . Заметим, что уравнение (1) в области является уравнением смешанного типа.
В этой статье рассматривается краевая задача для уравнения смешанного типа и приводится лемма для решения задачи, которая далее используется для доказательства устойчивости разностной модели, построенной для этой краевой задачи.
Для уравнения (1) изучаем следующую краевую задачу: Краевая задача: Найти функцию , удовлетворяющую в области уравнения (1), а при
Алоев Р. Д., Рахмонов Х. О., Шарипова Ш. Исследование разностной модели краевой задачи для уравнения смешанного типа.
В данной работе рассматривается проблема решения краевых задач для уравнений эллиптического типа. Эти задачи являются стационарными, так как в них отсутствует временная переменная.
Автоматизация решения задач данного типа во много раз ускорит учебный процесс и позволит студентам приобрести навыки математического и компьютерного моделирования различных физических процессов.
Решается первая начально-краевая задача для волнового уравнения.
Для дифференциальных уравнений различают три типа задач: задача Коши; краевая задача; смешанная задача.
Решения задачи Коши задается формулой Даламбера: . (4). В полуограниченной области для уравнение (2) мы можем ставить следующие краевые задачи...
Ключевые слова: краевая задача, линейный оператор, функционально-дифференциальное уравнение.
Аппроксимация первой краевой задачи разностной моделью для уравнения смешанного типа.
Задача Геллерстедта для общих линейных систем уравнений смешанного типа рассматривалась лишь в работе [6]. В ней рассматривается система вида.
Априорная оценка для решения первой краевой задачи для уравнения смешанного типа.
Библиографическое описание: Комилова Х. М. Задача Трикоми для уравнения параболо-гиперболического типа с нелокальными условиями склеивания
Отметим, что краевые задачи с нелокальными условиями склеивания для параболо-гиперболических уравнений известны в...
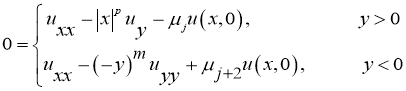
![]()
![]() - любые действительные числа, причем
- любые действительные числа, причем
![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]()
![]()
![]() при
при ![]() при
при![]()
![]() , ограниченнаяпри
, ограниченнаяпри ![]() отрезками
отрезками ![]() ,
, ![]() ,
, ![]() ,
, ![]() прямых
прямых![]() ,
,![]() ,
,![]() ,
,![]() соответственно, a при
соответственно, a при ![]() характеристиками
характеристиками
![]()
![]() ,
, ![]()
![]() ,
,
![]()
![]() ,
, ![]()
![]()
![]() проведем характеристиками
проведем характеристиками
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]()
![]()
![]()
![]() для уравнения
для уравнения ![]() исследуем следующую задачу:
исследуем следующую задачу:
![]()
![]() является регулярным решением уравнения
является регулярным решением уравнения ![]() в областях
в областях
![]() и
и ![]()
![]() ;
;
![]() причем
причем ![]() может обращаться бесконечность порядок
может обращаться бесконечность порядок![]() при
при ![]() и
и ![]() а при
а при![]() ограничена;
ограничена;
![]() на линии вырождения
на линии вырождения ![]() выполняется условия склеивания
выполняется условия склеивания
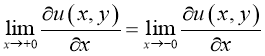 ,
, ![]()
![]()
![]() удовлетворяет краевым условиям
удовлетворяет краевым условиям
![]() ,
, ![]() ,
, ![]()
![]() ,
, 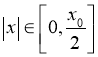 ,
, ![]()
![]() ,
, 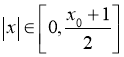 ;
; ![]()
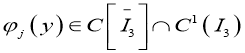 ,
, ![]()
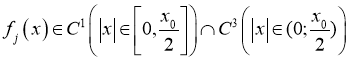 ,
, ![]()
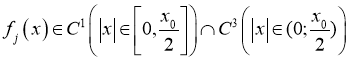 ,
,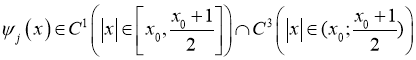 ,
, ![]()
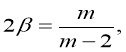 причем
причем
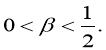
![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() то в области
то в области ![]() решение задачи G существует и единственно.
решение задачи G существует и единственно.







