Библиографическое описание:
Пожарский, Д. А. Генетический алгоритм для нахождения коэффициентов аппроксимации функции в контактных задачах для цилиндра / Д. А. Пожарский, Н. Б. Золотов, И. Е. Семенов. — Текст : непосредственный // Молодой ученый. — 2017. — № 24 (158). — С. 122-125. — URL: https://moluch.ru/archive/158/44625/ (дата обращения: 25.04.2024).
В ходе работы была рассмотрена контактная задача кручения полого линейно-упругого цилиндра в цилиндрических координатах. Рассмотрим цилиндр, внутренний радиус которого равен R, а внешний R1. Внешняя поверхность цилиндра жестко закреплена. Внутрь цилиндра помещен жесткий цилиндрический вкладыш длины 2a, к которому приложен крутящий момент M. Под действием этого момента упругий материал цилиндра в области контакта испытывает угловое перемещение u. Материал цилиндра характеризуется модулем сдвига G. При заданных величинах R, R1, a, требуется определить контактное напряжение p(z) в области контакта. Затем может быть определен момент M. При помощи интегрального преобразования Фурье задача сводится к следующему интегральному уравнению (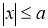 ) [3]:
) [3]:
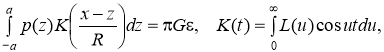 (1)
(1)
где символ ядра имеет вид
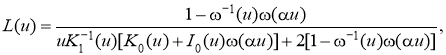 (2)
(2)
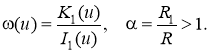
Здесь In(u), Kn(u) ― модифицированные функции Бесселя [10]. Безразмерный параметр характеризует толщину стенок цилиндра. При ∞ функция L(u) вида (2) стремится к функции
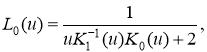 (3)
(3)
соответствующей случаю кручения пространства с цилиндрической шахтой.
Ранее было установлено, что при и u функция 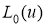 вида (3) достаточно хорошо аппроксимирует функцию L(u) и было получено полное решение уравнения (1) с символом ядра (3) [3]. Отметим, что наибольшее отличие этих функций наблюдается в нуле, где
вида (3) достаточно хорошо аппроксимирует функцию L(u) и было получено полное решение уравнения (1) с символом ядра (3) [3]. Отметим, что наибольшее отличие этих функций наблюдается в нуле, где
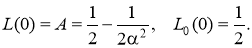 (4)
(4)
В бесконечности функция (2) имеет асимптотику:
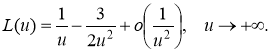
Асимптотическое решение. Введем безразмерные обозначения
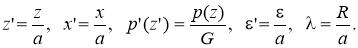 (6)
(6)
Штрихи далее будем опускать. Параметр характеризует относительную ширину области контакта. В обозначениях (6) уравнение (1) примет вид
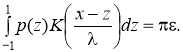 (7)
(7)
Для решения уравнения (7) применим сингулярный асимптотический метод [5,6], эффективный при достаточно малых значениях . Метод основан на сведении уравнения (7) к интегральному уравнению ВинераХопфа, при решении которого используем аппроксимацию
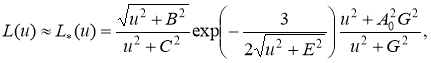 (8)
(8)
при условиях
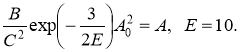 (9)
(9)
Аппроксимация (8), (9) учитывает поведение L(u) в нуле и бесконечности, см. формулы (4), (5). Кроме того, функция (8) легко факторизуема.
Для нахождения коэффициентов аппроксимации минимизируется невязка аппроксимации
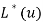
содержащая подгоночные коэффициенты
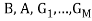
, заданная на множестве функции
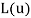
. Невязка определяется в соответствии с формулой
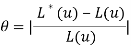
.
Таким образом, необходимо найти значения коэффициентов 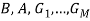 , при которых
, при которых 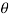 будет наименьшей.
будет наименьшей.
Практически всегда оптимизируемая функция обладает каким-либо свойством: алгоритмическое задание, сложная конфигурация допустимой области, наличие нескольких типов переменных. Это приводит к необходимости применения специализированных методов, к которым и относятся генетические алгоритмы, хорошо зарекомендовавшие себя в ситуациях, когда применение стандартных методов оптимизации крайне затруднено.
Литература:
-
Л. Галин. Развитие теории контактных задач в СССР. —:, 1976. — 496 с.
-
Гладков Л. А., Курейчик В. В., Курейчик В. М. Генетические алгоритмы. —: Физматлит, 2006. — 2006. с.
Основные термины (генерируются автоматически): интегральное уравнение, область контакта, символ ядра, функция.
Похожие статьи
Функция определяет ядро интегрального уравнения (1). Вычислим функцию и представим различные ее интерпретации.
при ; , где — обобщенная гипергеометрическая функция, — вырожденная гипергеометрическая функция, , , — символ Похгаммера, , , то соотношение...
Интегральным называется уравнение, в котором неизвестная функция стоит под знаком интеграла. Одномерное нелинейное интегральное уравнение первого рода относительно неизвестной функции имеет вид: , (1). где ядро и правая часть -заданные функции.
Через обозначим ядро типа Бергмана порядка s, — интегральный оператор с ядром типа Бергмана .
В последнем равенстве использовали 2π-периодичность подынтегральной функции. Итак
где — непрерывная и интегрируемая в функция. Приняв во внимание указанное выше, соотношение между и , из гиперболической части области D задачи запишем в виде.
Основные термины (генерируются автоматически): задача, интегральное уравнение.
где D- жесткость вязкоупругих пластин; интегральный оператор с ядрами релаксации R(t), т. е. )d — прогиб пластины
Нормализованное уравнение геометрии области для пластины, представленной на рис.1
Рвачев В. Л., Курпа Л. В. R-функций в задачах теории пластин.
где — радиальная часть волновой функции в соответствующих областях (i= 1 — ядро, i= 2 — оболочка); — сферические гармоники, l= 0,1,2…; m = 0,±1, ±2,…, ±l — орбитальное и
Радиальная часть удовлетворяет уравнению на функции Бесселя: 1) внутри ядра КТ.
Получен аналог уравнения Вайнберга для собственных функций оператора . Ключевые слова: модельный оператор
При этом получено очень мало результатов для таких гамильтонианов в том случае, когда ядро частично-интегрального оператора является невырожденным.
Исходя из этого требуется решить следующую интегральную уравнению Вольтерра методом вариационных итераций [3]. , , (2). где y(x) — искомая функция; f(x), F(y) — известные функции; K(x,t) — ядро интегрального уравнения (2).
-так называемое ядро релаксации. Линейная однородная система, (2).
Разлагая функцию в ряд Тейлора и учитывая, что получим уравнение. (23).
Об исследовании одного интегрального уравнения Вольтерра второго рода при заданных условиях.
Функция определяет ядро интегрального уравнения (1). Вычислим функцию и представим различные ее интерпретации.
при ; , где — обобщенная гипергеометрическая функция, — вырожденная гипергеометрическая функция, , , — символ Похгаммера, , , то соотношение...
Интегральным называется уравнение, в котором неизвестная функция стоит под знаком интеграла. Одномерное нелинейное интегральное уравнение первого рода относительно неизвестной функции имеет вид: , (1). где ядро и правая часть -заданные функции.
Через обозначим ядро типа Бергмана порядка s, — интегральный оператор с ядром типа Бергмана .
В последнем равенстве использовали 2π-периодичность подынтегральной функции. Итак
где — непрерывная и интегрируемая в функция. Приняв во внимание указанное выше, соотношение между и , из гиперболической части области D задачи запишем в виде.
Основные термины (генерируются автоматически): задача, интегральное уравнение.
где D- жесткость вязкоупругих пластин; интегральный оператор с ядрами релаксации R(t), т. е. )d — прогиб пластины
Нормализованное уравнение геометрии области для пластины, представленной на рис.1
Рвачев В. Л., Курпа Л. В. R-функций в задачах теории пластин.
где — радиальная часть волновой функции в соответствующих областях (i= 1 — ядро, i= 2 — оболочка); — сферические гармоники, l= 0,1,2…; m = 0,±1, ±2,…, ±l — орбитальное и
Радиальная часть удовлетворяет уравнению на функции Бесселя: 1) внутри ядра КТ.
Получен аналог уравнения Вайнберга для собственных функций оператора . Ключевые слова: модельный оператор
При этом получено очень мало результатов для таких гамильтонианов в том случае, когда ядро частично-интегрального оператора является невырожденным.
Исходя из этого требуется решить следующую интегральную уравнению Вольтерра методом вариационных итераций [3]. , , (2). где y(x) — искомая функция; f(x), F(y) — известные функции; K(x,t) — ядро интегрального уравнения (2).
-так называемое ядро релаксации. Линейная однородная система, (2).
Разлагая функцию в ряд Тейлора и учитывая, что получим уравнение. (23).
Об исследовании одного интегрального уравнения Вольтерра второго рода при заданных условиях.
![]() ) [3]:
) [3]:
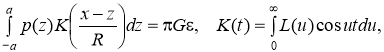 (1)
(1)
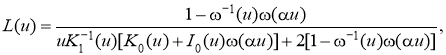 (2)
(2)
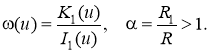
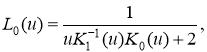 (3)
(3)
![]() вида (3) достаточно хорошо аппроксимирует функцию L(u) и было получено полное решение уравнения (1) с символом ядра (3) [3]. Отметим, что наибольшее отличие этих функций наблюдается в нуле, где
вида (3) достаточно хорошо аппроксимирует функцию L(u) и было получено полное решение уравнения (1) с символом ядра (3) [3]. Отметим, что наибольшее отличие этих функций наблюдается в нуле, где
![]() (4)
(4)
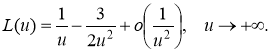
![]() (6)
(6)
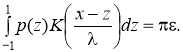 (7)
(7)
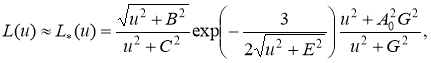 (8)
(8)
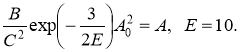 (9)
(9)
![]() , при которых
, при которых ![]() будет наименьшей.
будет наименьшей.







