Для современных листовых офсетных машин характерно применение принудительного привода между цилиндрами, который, однако, не освобождает их от проскальзывания в контактной зоне. Это вызвано тем, что помимо кинетической связи зубчатого привода в контактной зоне присутствует фрикционное взаимодействие упругой и жесткой оболочки цилиндров. Наличие подобной двойственной связи требует соблюдения равенства передаточных отношений зубчатой и фрикционной передач, что реально трудно осуществить на практике. Поэтому необходимо провести анализ научных трудов, в которых рассматривалось фрикционное взаимодействие между цилиндрами.
Условия фрикционного контакта цилиндров определяют качество работы печатного аппарата с принудительным приводом. Одной из причин снижения качества является упругое проскальзывание цилиндров в зоне контакта. Исследование упругого проскальзывания между цилиндрами в научных работах, посвященных этому вопросу, ведется в представлении о проскальзывании во фрикционных парах качения цилиндра по цилиндру.
В этих исследованиях рассматриваются вопросы продольного проскальзывания контактируемых поверхностей под действием упругой деформации оболочек с учетом кривизны взаимодействующих тел [1–4] при их перекатывании с учетом упругого взаимодействия [5].
Первое экспериментальное исследование явления качения выполнено Кулоном (Coulomb C. A.). Вывод о пропорциональности силы сопротивления нормальной нагрузке явился основным результатом его опытов. Им показана зависимость силы сопротивления от геометрических размеров перекатываемого тела.
Следующим шагом изучения вопроса о контактном взаимодействии явилась теория О. Рейнольдса (Reynolds O.) о продольном проскальзывании при качении [6]. В работе отмечено, что деформация поверхностей тел во время качения сопровождается неодинаковыми перемещениями, но эффект скольжения позволяет им деформироваться после того, как они вошли в контакт. Скольжение поверхностей сопровождается трением. Появляется сопротивление качению, которое должно быть пропорционально работе сил трения и, соответственно, коэффициенту трения между поверхностями.
Одним из важных выводов теории Рейнольдса является понятие об упругом скольжении. Вводя понятие геометрического расстояния, прошедшего при качении цилиндрическим телом, Рейнольдс показал наличие упругого скольжения, в связи с чем, длина пути, проходимая за один оборот цилиндра, отличается от длины его окружности. В случае ведущего цилиндра длина пути меньше геометрического, в случае ведомого — больше геометрического. Отношение разности между геометрическим расстоянием и фактическим расстоянием к геометрическому расстоянию представляет собой величину относительного упругого проскальзывания. Оно зависит от формы тел и воспринимаемых ими усилий и моментов.
Важным вкладом в исследования качения являются работы выдающихся отечественных ученых Н. П. Петрова [7] и Н. Е. Жуковского [8].
Ими установлено наличие зон скольжения и сцепления на линии контакта перекатываемых тел. Сила тяги передается только в зонах скольжения, где силу трения можно описать законом Кулона, а в зонах сцепления сила тяги не развивается.
А. Ю. Ишлинский [4] рассматривал качение абсолютно жесткого цилиндрического колеса по упрощенной модели упругого основания, составленного из элементарных стержней. Решение задачи А. Ю. Ишлинский проходит исходя из результатов исследования Рейнольдса.
Передача тянущего усилия от жесткого цилиндра к цилиндру с эластичным покрытием сопровождается деформацией последнего в зоне контакта (рис. 1). При этом различают нормальную деформацию, возникающую от усилия прижима цилиндров, и тангенциальную деформацию, являющуюся, в основном, следствием действия сил сопротивления повороту. В результате деформаций в пределах упругости возникает упругое проскальзывание цилиндров. При этом в зоне контакта 2а наблюдается участок сцепления (![]() ). На этом участке тангенциальные деформации цилиндров одинаковы.
). На этом участке тангенциальные деформации цилиндров одинаковы.
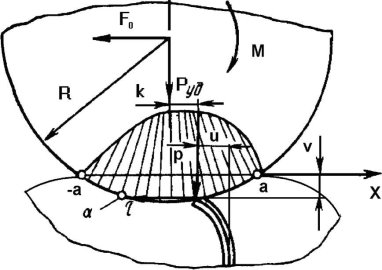
Рис. 1. Модель контакта упругого основания с жестким валком
На участке скольжения (![]() ) тангенциальная деформация тел, находящихся в контакте, различна, вследствие чего наблюдается упругое проскальзывание.
) тангенциальная деформация тел, находящихся в контакте, различна, вследствие чего наблюдается упругое проскальзывание.
Таким образом, упругое проскальзывание, или его относительную величину можно определить по следующей формуле:
![]() ,(1.1)
,(1.1)
где ![]() — длина пути, пройденная цилиндром с эластичным покрытием за один оборот приводного цилиндра;
— длина пути, пройденная цилиндром с эластичным покрытием за один оборот приводного цилиндра;
![]() — радиус приводного цилиндра.
— радиус приводного цилиндра.
В модели А. Ю. Ишлинского тангенциальные ![]() и нормальные
и нормальные ![]() смещения вершин основания принимались пропорционально соответственным удельным касательным
смещения вершин основания принимались пропорционально соответственным удельным касательным ![]() и нормальным усилиям
и нормальным усилиям ![]() :
:
![]() (1.2)
(1.2)
В первом приближении модель А. Ю. Ишлинского может служить аналогом ротационной печатной пары.
Н. И. Глаголевым исследовалась задача о сопротивлении перекатыванию упругого цилиндрического тела по упругому основанию [3]. В формировании задачи определяется, что сопротивляемость перекатыванию объяснено трением скольжения ввиду относительного сдвига точек на поверхности соприкосновения. Для формирования уравнений задачи были выбраны математические методы, внедренные Н. И. Мусхелишвили [9].
Уравнения для расчета упругого проскальзывания, контактных давлений ![]() и касательных усилий
и касательных усилий ![]() , полученные Н. И. Глаголевым:
, полученные Н. И. Глаголевым:
![]() ;(1.3)
;(1.3)
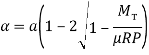 ;(1.4)
;(1.4)
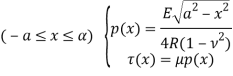 ;(1.5)
;(1.5)
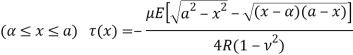 (1.6)
(1.6)
где E и ![]() — модуль Юнга и коэффициент Пуассона материала эластичного слоя;
— модуль Юнга и коэффициент Пуассона материала эластичного слоя;
Мт, P, р(х) и (х) — удельные (отнесенные к ширине цилиндров) момент от сил сопротивления повороту, сила прижима цилиндров;
— коэффициент трения.
Полученные им выражения показывают, что при установившемся упругом качении цилиндра ширина линии контакта не зависит от величины воспринимаемого им момента и определяется точно так же, как в задаче о статическом давлении без учета сил трения. Ширина зоны сцепления изменяется от величины линии контакта, при отсутствии тягового момента до нуля, что соответствует началу буксования. Сила тяги изменяется от нуля до максимального значения, определяемого нормальной нагрузкой и коэффициентом трения, при изменении тягового момента от нуля до максимального значения. Ведущий цилиндр жесткий, в отличие от ведомого, реализует максимальную силу тяги меньшим моментом, чем при прочих равных условиях цилиндр менее жесткий.
Р. В. Вирабов [1], используя модель А. Ю. Ишлинского, получил решение задачи о качении колеса из эластичного материала по жесткому основанию, что является аналогом плоскопечатного аппарата:
Расчеты тяговой способности фрикционного контакта тел в условиях качения и скольжения выполняются на основе результатов решения контактных задач теории упругости. В инженерной практике известны различные подходы к решению прикладных контактных задач. Первые из них — упомянутые выше аналитические решения, основанные на математических методах теории упругости.
Вместе с тем, деформации полимерных материалов зависят не только от величины воспринимаемых усилий, но и от скорости их приложения и продолжительности контакта. Решению контактной задачи о трении качения с учетом реологических свойств материалов взаимодействующих тел посвящены работы Ю. Н. Работнова [10], Н. И. Глаголева [11], Л. А. Галина [2], Э. В. Теодоровича [12]. Практическое использование их результатов требует экспериментального определения параметров, характеризующих реологические свойства (коэффициента гистерезисных потерь, времен упругого последействия и релаксации напряжений и др.).
Стремление к увеличению точности расчетов деталей и узлов машин приводит к рассмотрению их геометрических размеров и, в связи с этим к новым постановкам контактных задач теории упругости, которые принято называть “неклассическими”. Например, задачи расчета прочности и износа деталей с покрытиями и механизмов, передающих движение через контакт трения качения и скольжения и др. приводятся к интегральному уравнению.
Рассматриваемая задача описывается интегральным уравнением первого рода [13]:
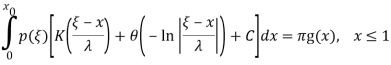 ,(1.7)
,(1.7)
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, 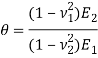 ;
;
b — толщина эластичного слоя;
— максимальная деформация эластичного слоя.
Решения, полученные Г. Я. Поповым [14], В. М. Александровым [13], Вангом (C. F. Wang) [15] используют асимптотические методы, в связи, с чем накладывают ограничения на геометрические параметры рассматриваемых тел. Точные решения удается получить для ограниченного числа практических применений.
Известны численные решения контактных задач с помощью метода конечных элементов, линейного и нелинейного программирования [16], сопряженного градиента [17]. В настоящее время нет единого мнения относительно наилучшего метода, пригодного для широкого применения инженерами-практиками. Обзор методов решения контактных задач и полученных результатов содержится в монографиях [16, 18].
Проведенный краткий анализ научных исследований, связанных с фрикционным взаимодействием контактируемых тел позволил проиллюстрировать сложность физических явлений контактной зоны.
Литература:
- Вирабов Р. В. Тяговые свойства фрикционных передач. М.: Машиностроение. 1982. 263 с.
- Галин Л. А. Контактные задачи теории упругости и вязкоупругости. М.: Наука. 1980. 304 с.
- Глаголев Н. И. Трение и износ при качении цилиндрических тел. М.: Инженерный журнал, 1964. т. 4, вып. 4.
- Ишлинский А. Ю. О проскальзывании в области контакта при трении качения. М.: Известия АН СССР, ОТН, 1956. № 6, С. 3–15.
- Вирабов Р. В. Сравнительная оценка составляющих сопротивления качению упругих тел. М.: Вестник машиностроения. 1972. № 4, С. 18–22.
- Reynolds O. On mlling-friction, Philos. Trans. of Sosienty of London, 1876. Vol. 166, p. 1.
- Петров Н. П. О непрерывных тормозных системах. С-Петербург: Изв. Петерб. проект. технол. ин-та,. 1878.
- Жуковский Н. Е. О скольжении ремня на шкивах. М.: тип. Волчанинова. 1894. 25 с.
- Мусхелишвилли Н. И. Некоторые основные задачи математической теории упругости. СССР: Изд. АН. 1954. 690 с.
- Работнов О. Н. Равновесие упругой среды с последействием. — Прикладная математика и механика. М.: 1948, т. 12, № 1.
- Блохина А. И., Глаголев Н. И., Томило Э. А. Приближенное решение контактной задачи о трении качения с учетом реологических свойств материалов взаимодействующих тел. М.: Машиноведение. 1972. № 6. С. 61–67.
- Теодорович Э. В. Скольжение цилиндра по вязкоупругому основанию. М.: Прикладная математика и механика. 1978. Вып. 2 С. 367- 371.
- Александров В. М., Мхитарян С. М. Контактные задачи для тел с тонкими покрытиями и прослойками. М.: Наука, 1983. 488 с.
- Попов Г. Я. Об одном приближенном способе решения некоторых плоских задач теории упругости. Арм. ССР: Изв. АН. Сер. физ — мат. наук. 1961. № 3.
- Ванг (C. F. Wang). Упругий контакт полосы, сдавленной двумя цилиндрами. Прикладная механика, 1968. № 2. с. 73–79.
- Джонсон К. (K. L. Jonson). Механика контактного взаимодействия. Пер. с англ. — М.: Мир. 1989. 510 с.
- Маркс (W. R. Marks), Саламон (N. J. Salamon). Усовершенствованный метод сопряженного градиента для решения контактных задач без трения. М.: МИР. Конструирование. 1983. т. 105, № 2, с. 73- 78.
- Трение, Изнашивание, смазка: Справочник. В 2-х кн. / Под. ред. И. В. Крагельского, В. В. Алисина. — М.: Машиностроение. 1978.

