Рассмотрим в области ![]() , с границей
, с границей ![]() и
и ![]() — цилиндр, с боковой гранью
— цилиндр, с боковой гранью ![]() .
.
Ставится задача найти решение следующих уравнений [1], [2]:
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
здесь (1) — уравнение движения, (2) — закон импульса, (3), (4) — уравнения состояния: (3) — вязкоупругая среда Максвелла, (4) — уравнение Кельвина-Фойгта; B — матрица коэффициентов Ламе, симметричная, положительно определенная, С — матрица, состоящая из коэффициентов вязкости, симметричная, положительно определенная, ![]() — диагональная матрица,
— диагональная матрица, ![]() — вектор скоростей, * — означает транспонирование,
— вектор скоростей, * — означает транспонирование, ![]() — вектор напряжений,
— вектор напряжений, ![]() — вектор деформаций; опорный оператор R определяется следующим образом [1]:
— вектор деформаций; опорный оператор R определяется следующим образом [1]:
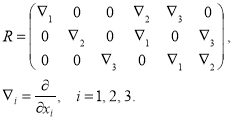 (5)
(5)
Матрицы В, С, ![]() — перестановочны.
— перестановочны.
К соотношениям (1)-(4) нужно добавить соотношения перемещение-деформации: ![]() . Вектор перемещения u и скорости v связаны соотношением
. Вектор перемещения u и скорости v связаны соотношением ![]() .
.
После несложных преобразований приходим к уравнениям:
![]() (6)
(6)
для среды Максвелла,
![]() (7)
(7)
для среды Кельвина-Фойгта.
Решение задачи (1)-(3), (6) будем искать в цилиндре ![]() . При этом
. При этом
![]() (8)
(8)
![]() (9)
(9)
Предположим, что на боковой поверхности цилиндра Q искомое решение удовлетворяет одному из приведенных ниже однородных краевых условий;
![]() (10)
(10)
Начальные данные (8), (9) и краевые условия (10) будем считать согласованными. При этом задачу (1)-(3), (6) назовем задачей (I), а задачу (1), (2), (4), (7) — задачей (II).
Как известно, если ![]() , то справедлива оценка
, то справедлива оценка
![]() (11)
(11)
В соответствии с методом фиктивных областей [3], [4], дополним исходную область D некоторой областью ![]() до составной области
до составной области ![]() с границей
с границей ![]() .
.
В составной области ![]() рассмотрим задачу:
рассмотрим задачу:
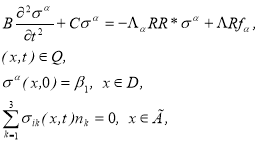 (12)
(12)
где ![]() — малый параметр и
— малый параметр и
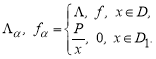
На границе ![]() ставятся условия согласования:
ставятся условия согласования:
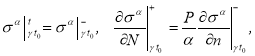 (13)
(13)
где 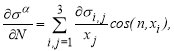 n — вектор нормали к границе
n — вектор нормали к границе ![]() , знаки «+» или «-» означают стремление функции изнутри и извне границы
, знаки «+» или «-» означают стремление функции изнутри и извне границы ![]() . Параметр P принимает значение 1 или -1.
. Параметр P принимает значение 1 или -1.
Тогда справедлива следующая теорема.
Теорема 1. Верна оценка
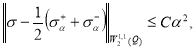 (14)
(14)
Здесь ![]() и
и ![]() соответствуют решению задачи (12), (13) и отвечают значению параметра
соответствуют решению задачи (12), (13) и отвечают значению параметра ![]() и
и ![]() .
.
Доказательство. Рассмотрим следующие ряды: ![]() в области Q,
в области Q, ![]() в области
в области ![]() . Ряды
. Ряды ![]() ,
, ![]() являются абсолютно сходящимися при достаточно малых
являются абсолютно сходящимися при достаточно малых ![]() .
.
В самом деле, для определения функций ![]() ,
, ![]() получаем
получаем
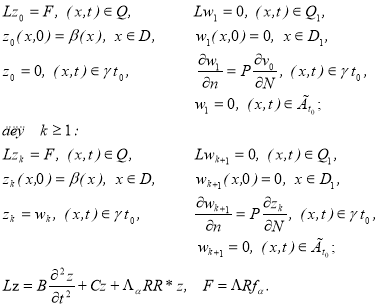 (15)
(15)
Решения (15) ![]() имеем из теории неоднородных задач [5]
имеем из теории неоднородных задач [5]
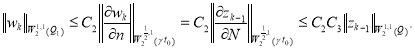 (16)
(16)
Далее получим сходимость рядов ![]() ,
, ![]()
![]()
Учитывая (11), (16), получим:
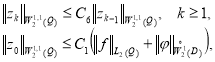 (17)
(17)
где ![]() .
.
Если ![]() , то ряд
, то ряд ![]() абсолютно сходится в Q, а ряд
абсолютно сходится в Q, а ряд ![]() абсолютно сходится в норме
абсолютно сходится в норме ![]() .
.
Теорема 2. Если ![]() , то справедлива следующая оценка:
, то справедлива следующая оценка:
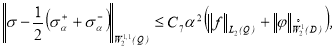 (18)
(18)
где ![]() и
и ![]() — решения задачи (12), (13) при
— решения задачи (12), (13) при ![]() и
и ![]() ,
, ![]() — решение задачи (I).
— решение задачи (I).
Доказательство. На основании теоремы 1 имеем
![]() (19)
(19)
где ![]() ,
, ![]() соответствуют параметру
соответствуют параметру ![]() .
.
Соответственно на основании теоремы 1 имеем
![]() (20)
(20)
где ![]() ,
, ![]() соответствуют параметру
соответствуют параметру ![]() .
.
Очевидно, что ![]() — решение задачи I.
— решение задачи I.
Введем обозначения
![]()
тогда для функции ![]() получим задачу
получим задачу
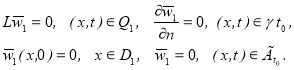
Отсюда получаем ![]() или
или ![]() .
.
Введем функцию ![]() где
где ![]() удовлетворяет задаче
удовлетворяет задаче
![]()
Отсюда получаем ![]() и, следовательно,
и, следовательно, ![]() .
.
Далее, определим ![]() имеем
имеем ![]() . Продолжая аналогичные рассуждения, получим
. Продолжая аналогичные рассуждения, получим
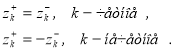 (21)
(21)
Учитывая (21), подставляя в (19), (20), получим в Q:
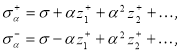 (22)
(22)
Используя (17) и разложение (22), получаем при ![]()
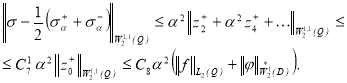
Для задачи II в соответствии с методом фиктивных областей построим вспомогательную задачу
![]() (23)
(23)
Дополним начальными и краевыми условиями из (12) и условия сопряжения (13).
Для задачи II верна
Теорема 3. Для ![]() верна оценка
верна оценка
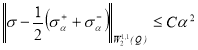 .(24)
.(24)
Доказательство аналогично доказательству теоремы 1.
Кроме того, справедлива
Теорема 4. Если ![]() , то верна следующая оценка
, то верна следующая оценка
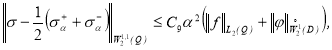 (25)
(25)
где ![]() — решение задачи II,
— решение задачи II, ![]() и
и ![]() — решения задачи (23) при
— решения задачи (23) при ![]() и
и ![]() .
.
Доказательство аналогично доказательству теоремы 2.
Запись исходных задач в терминах оператора ![]() и сопряженного
и сопряженного ![]() , обусловлены возможностью построения консервативных разностных схем, допускающих реализацию с помощью схем расщепления.
, обусловлены возможностью построения консервативных разностных схем, допускающих реализацию с помощью схем расщепления.
Литература:
- Букенов М. М., Кузнецов Ю. А. Об одной спектральной задаче теории упругости. // ВЦ СО АНСССР, Препринт, Новосибирск, 1981г. — 13 с.
- Букенов М. М. Постановка динамической задачи линейной вязкоупругости в скоростях напряжениях. // Сиб. Журнал вычислительной математики РАН. Сиб. Отд. — Новосибирск, 2005. — т.8, № 4. — с. 289–295.
- Коновалов А. Н. Об одном варианте метода фиктивных областей. // В кн. Некоторые проблемы вычислительной и прикладной математики. — Новосибирск, 1975, с. 191–199.
- Букенов М. М. Метод фиктивных областей для среды Максвелла. // Численные методы и пакеты программ для решений уравнений математической физики. — Новосибирск, 1985 — т. 4, № 2. — с. 117–126.
- Ладыженская О. А. Линейные и квазилинейные уравнения параболического типа. — Москва: Наука. — 1967. — 736 с.

