На основе модели качения упругого колеса М. В. Келдыша рассмотрены вопросы влияния упругости промежуточного колеса на стационарное движение вариатора и на программное движение экипажа по плоскости. При такой постановке задач параметры деформаций колеса рассматриваются как дополнительные возмущения. Анализ условий устойчивости стационарного движения редуктора с промежуточным колесом с упругой периферией оказываются совсем другими, чем в случае твердого промежуточного колеса. Также рассмотрен вопрос отклонения от кругового программного движения экипажа с ведущим упругим колесом. Численный анализ уравнений движения экипажа показывает, что при больших значениях угловой скорости собственного вращения колеса, отклонения центра колеса, от программного увеличивается существенно.
Как известно, для исследования систем, содержащих упругие колеса, из-за сложности аналитических выкладок предложены дискретные модели качения, которые с достаточной степенью точности описывают динамику систем с качением. К таким моделям относятся модели И. Рокара, Грайдануса, М. В. Келдыша и другие, где деформируемость колеса учитывается конечным числом параметров, силы реакций предполагаются пропорциональными параметрами, массой деформируемой части пренебрегают [1]. Ниже с помощью модели качения М. В. Келдыша [2] исследуется динамика классического фрикционного редуктора с промежуточным колесом рассмотренного в работе И.Лурье [3], и задача отклонения от программного движения экипажа с ведущим колесом по горизонтальной плоскости. Предполагается, что колесо представляет собой диск с упругой периферией. Оно расположено на оси симметрии пластинки и движется без проскальзывания. Два остальных колеса рояльные. Они не ограничивают движение пластинки по плоскости.
Рассмотрим вопрос влияния упругости промежуточного колеса на устойчивость стационарных движений редуктора скорости. При указанных предположениях [3] исследование системы можно проводить в рамках динамики неголономных систем с идеальными связями, так как сумма элементарных работ сил реакций на виртуальных перемещениях системы равна нулю. Так как массой деформируемой части пренебрегаем, то энергия ускорений вариатора будет такой же, как в твердом случае [3].
S=![]() ώ1 [J2
ώ1 [J2 ![]() J1 + J
J1 + J ![]() +
+ ![]() mгр (4l2-x2)] — ώ1ω1Ẋ (
mгр (4l2-x2)] — ώ1ω1Ẋ (![]() + mгрx) +
+ mгрx) + ![]() x«2 (m+
x«2 (m+ ![]() ) + mгрx»·x'(
) + mгрx»·x'(![]() ω2 +
ω2 + ![]() )
)
Здесь введены следующие обозначения: J1,J2, J — соответственно моменты инерции барабана, диска и промежуточного колеса; р- расстояние от оси второго диска до точки контакта; с1,с2 — жесткости пружин; mгр — масса груза. Будем предполагать, что проскальзывание площадки контакта в продольном и поперечном направлениях отсутствует, то есть имеем случай качения без проскальзывания. Уравнения связей с учетом поперечной деформации и поворота оси площадки контакта примут следующий вид [2]: Ẋ — λ =r1Ψ ω1, r1 ω1 = р ω2, Ψ = (α λ + βΨ)R ω1
В соотношениях (2) первые два уравнения представляют собой условия отсутствия проскальзывания центра контакта в продольном и поперечном направлениях, а третье уравнение связывает радиус кривизны линии качения с параметрами деформации λ и Ψ (модель качения упругого колеса М. В. Келдыша), где λ — поперечная составляющая смещения центра контакта колеса, Ψ — угол между касательной к линии качения и плоскостью промежуточного колеса. Уравнения движения в форме Аппеля принимает следующий вид:
θ (х) ώ1 — F (x) Ẋ ω1 = М1 + ![]() M2+
M2+![]() + r1a Ψ λ + b Ψr1 (α λ+ β Ψ)),
+ r1a Ψ λ + b Ψr1 (α λ+ β Ψ)),
m(x)x» +![]() mгрx ω12
mгрx ω12 ![]() mгр Ẋ 2 = -(с1+с2) (х-х0) — с1 δ1 +с2δ2 + a λ,
mгр Ẋ 2 = -(с1+с2) (х-х0) — с1 δ1 +с2δ2 + a λ,
Ẋ — λ=r1 ω1 Ψ, Ψ=(α, λ + βΨ)r1ω1.
где: θ(х) = [J2![]() + J1+ J
+ J1+ J![]() +
+ ![]() mгр(4l2-x2)], m(x)=m +
mгр(4l2-x2)], m(x)=m + 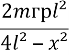 ,
,
F(x) = (![]() +mгрх)
+mгрх)
a, b, α,β — коэффициенты пропорциональности, δ1, δ2 — начальные натяжения пружин. Частное решение дифференциальных уравнений вариатора получим, полагая
ω1 = ω10, х=х0, λ= Ψ=0.
Подставляя (5) в уравнения движения (4), получим
М1+![]() M2 = 0,
M2 = 0, ![]() mгрx0 (ω10)2 = — c1δ1+с2δ2.
mгрx0 (ω10)2 = — c1δ1+с2δ2.
Соотношения (3) представляют собой условия осуществимости частного решения (4). Уравнения движения (3) можно трактовать как уравнения движения в окрестности частного решения (4) с учетом упругости промежуточного колеса. При этом уравнения первого приближения имеют вид:
θ (х) ώ1'- F (x0) Ẋ 'ω10 + ![]() М2x' —
М2x' — ![]() =0
=0
m(x0)ẍ' +![]() mгр x' (ω10)2 +mгр х0 ω10 ω1' + (c1+c2) x' + a λ=0,
mгр x' (ω10)2 +mгр х0 ω10 ω1' + (c1+c2) x' + a λ=0,
Ẋ ' — λ — r1 ω10 Ψ = 0, Ψ- r1 ω10αλ — r1 ω10 β Ψ=0.
Характер движения в окрестности частного движения определяется корнями характеристического уравнения линейного приближения. Движение экипажа по плоскости с упругим ведущим колесом реализация программных движений с помощью сил реакций условных связей и параметров управлений в механических системах в настоящее время является актуальной задачей. Рассмотрим программное движение экипажа с ведущим колесом по горизонтальной плоскости. предполагая, что ведущее колесо расположено на оси симметрии пластинки и движется без проскальзывания, а два остальных колеса рояльные, то есть не ограничивают движение пластинки по плоскости. Для определения положения системы введем следующие обобщенные координаты: х,у — координаты центра масс пластинки, θ — угол между осью симметрии пластинки и координатной осью Ох, θ1 — угол между линией пересечения плоскости ведущего колеса и плоскостью движения с координатной линией Ох, ω1 — собственная угловая скорость колеса. Рассмотрим отклонение механической системы с ведущим деформируемым колесом относительно программного движения. При этом параметры деформаций будем трактовать как возмущающие факторы. Пусть система движется под действием параметров управления определяемыми в случае, когда ведущее колесо является абсолютно твердым телом. Исследуем отклонение системы от программного движения за счет упругости ведущего колеса.
В рассматриваемой задаче первое условие, отсутствие проскальзывание центра контакта (ro1+ξ)t=vk= ω1·r·j1 полностью сохраняется. А второе условие, как нам известно, имеет место при малых отклонениях от прямолинейного движения. Если разложить коэффициент кривизны линии качения колеса в окрестности 1/R0, сохраняя при этом первое приближение по отношению к параметрам деформаций получим:
![]() =
=![]() =
=![]() + αξ-β
+ αξ-β![]() ,
,
где![]() — это кривизна программного движения твердого ведущего колеса, α,β — коэффициенты пропорциональности. На основании теории М. В. Келдыша система сил реакций плоскости эквивалента продольной силе Rx1, направленной вдоль оси О1х1, поперечной силе Rх1= k·ξ, пропорциональной боковой деформации колеса ξ и направленной вдоль оси 01у1, и моменту MΨ=k1·Ψ. Уравнения движения в форме уравнений Лагранжа 1-рода примут вид.
— это кривизна программного движения твердого ведущего колеса, α,β — коэффициенты пропорциональности. На основании теории М. В. Келдыша система сил реакций плоскости эквивалента продольной силе Rx1, направленной вдоль оси О1х1, поперечной силе Rх1= k·ξ, пропорциональной боковой деформации колеса ξ и направленной вдоль оси 01у1, и моменту MΨ=k1·Ψ. Уравнения движения в форме уравнений Лагранжа 1-рода примут вид.
![]() ((mn+mk)·x» — a·mk(sin)θ* θ''+θ'2 cosθ)) = λ1=Rx1sinθ1+ Ry1cosθ1,
((mn+mk)·x» — a·mk(sin)θ* θ''+θ'2 cosθ)) = λ1=Rx1sinθ1+ Ry1cosθ1,
![]() ((mn+mk)·ÿ +a·mk(-cosθ·θ''+θ'2 sinθ)) = λ2=-Rx1cosθ1+Ry1sinθ1,(8)
((mn+mk)·ÿ +a·mk(-cosθ·θ''+θ'2 sinθ)) = λ2=-Rx1cosθ1+Ry1sinθ1,(8)
Jz1·θ''1=u10+M Ψ, Jx1· ω'1=-Ry1·r+u20,
J'n·θ''+ mk·a(ÿ·cos θ-x» ·sin θ)=- (λ1·sin θ- λ2·cosθ)+u30.
Где u10, u20, u30,параметры управления, которые реализуют программное движение с твердым колесом. Присоединив к этим уравнениям кинематические связи
Ẋ =asin θ· θ' — (ξsinθ1)'t + ω1r cos (Ψ+θ1) = asin θ· θ'-ξ'1+ ω1r cos (Ψ+θ1),
ý= -acos θ· θ'+(ξcosθ1)'t + ω1r sin (Ψ+θ1)= acos θ· θ'+ξ'y +ω1r sin (Ψ+θ1),
![]() =
=![]() =
=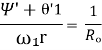 + αξ — β
+ αξ — β![]() ,(9)
,(9)
получим замкнутую систему обыкновенных дифференциальных уравнений относительно переменных θ, θ1, ω1,x, y, Ry1, ξ,Ψ. Таким образом, при постановке задачи качения колеса с упругой периферией условия устойчивости стационарного движения регулятора оказываются совсем другими, чем в случае твердого промежуточного колеса. При этом параметры деформации колеса можно представить как дополнительные возмущения. Анализ характеристического уравнения первого приближения движения редуктора в окрестности стационарного движения показывает, что возможны случаи самовозбуждения промежуточного колеса, которое приводит к неустойчивости движения. Численный анализ уравнений движения экипажа с упругим промежуточным колесом показывает, что при больших значениях угловой скорости собственного вращения колеса, отклонения центра колеса, от программного увеличивается существенно.
Литература:
- Тураев Х. Т., Фуфаев Н.А, Мусарский Р. А. Теория движения систем с качением.- Ташкент: Фан, 1987. — 158с.
- Келдыш М. В. Шими переднего колеса трехколесного шасси. Труды ЦАГИ. 1945 № 584.С. 1–33.
- Лурье А. И. Аналитическая механика. — М.: Гостехиздат, 1961. -824 с.

