Анализ работы механизма с накопителем энергии с силовым замыканием

Во многих механизмах машин текстильной и легкой промышленности в качестве рабочего движения используется возвратно-поступательное или качательное движение. Если закон движения этих механизмов является гармоническим без выстоя или мало отличающийся от него, то имеется возможность значительного снижения инерционных нагрузок в кинематических парах механизма за счет использования упругих накопителей энергии.

При использовании упругих накопителей энергии возникает вопрос: каким образом выбирать параметры накопителя (упруга элемента), чтобы он наилучшим образом удовлетворял условиям эксплуатации механизма с силовыми замыканиями?

Для выяснения этого вопроса рассмотрим простейшую динамическую модель механизма с накопителем. При этом предполагаем, что ведомые и ведущие звенья абсолютно жесткие, масса (момент инерции массы) ведомой части механизма и жесткость накопителя являются сосредоточенными параметрами, не изменяющимся с течением времени.

Как показали практические расчеты, модель, указанная на рисунке 1 удовлетворительно описывает работу достаточно большого числа механизмов периодического движения, используемых в машинах текстильной и легкой промышленности.

Рассмотрим случай, когда имеет место силовое замыкание за счет использования энергии упругого элемента с линейной характеристикой. Сопротивление движению ведомой части механизма пропорционально скорости её перемещения с коэффициентом пропорциональности η.

Так как упругий элемент должен постоянно находиться в контакте с ведомой массой, то за начало отсчета выбираем кране положение ведущего звена 1

Для обеспечения надежного и постоянного контакта упругого элемента (пружины) с ведомым звеном дадим ему в крайнем положении механизма предварительное сжатие (натяг) на величину X_0.

Для правильного функционирования механизма необходима обеспечить безотрывное движение ведомой, части механизма с массой m от ведущей. Выведем условия, которым должны удовлетворять параметры механизма и накопителя для безотрывной работы. Для этого запишем уравнение движения массы m с учетом силы тяжести.

Уравнение движения массы m имеет вид:

Р_и + Р_с+ Р_у± mg + R =0                                                                                              (1)

где Р_и = — mx₁; Р_с= — η x₁; Р_у= — k(x₁+x₀)

R — реакция со стороны ведущей части механизма на ведомую.

Подставляя эти выражения в формулу (1), получим (здесь и далее считается, что сила тяжести прижимает ведомую часть механизма к ведущей):

R= mx₁+ ηx₁+ k(x₁+x₀)+ mg                                                                                       (2)

Движение без отрыва ведомой части механизма с массой m от ведущего звена 1 запишется в виде неравенства R ≥ 0.

Для простоты рассмотрим случай, когда ведущее звено движется по гармоническому закону с частотой ω. Тогда (нижнее положение принято за начало отсчета):

Х₁=а(1-cosωt), (3)

где а — амплитуда движения звена 1 (рис.1).

Подставляя вқражение Х₁ в формулу (2), будем иметь:

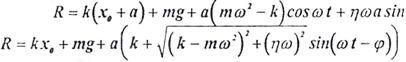
или

В этом выражении R зависит от k и x_0.Ясно, что конструктору желательно подобрать такие k и x₀,которые на рабочей ω= ω₁ частоте механизма доставляли бы минимум наибольшему амплитудному (при sin(ω₁t-φ)=1) значению R=R_1.Следовательно, R=R₁нужно рассматривать как функцию двух переменных, т. е. R₁(k,x₀).

В то же время для нормальной работы механизма необходима чтобы наименьшее амплитудное (при sin(ω₁t-φ)=1) значение R=R₂ ≥ 0.Далее будем рассматривать «критический случай», когда R₁(k,x₀)=0. Таким образом, имеем функцию (без учета силы тяжести):

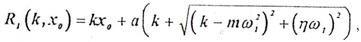
для который хотим подобрать параметры k и х₀, доставляющие ей минимум, и функцию (уравнение связи):

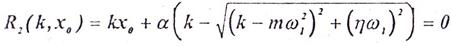
В математическом плане задача свелась к нахождению условного экстремума функции R₁(k,x₀). Ее можно представить так: из всех точек линии R₂(k,x₀)=0 нужно найти такую точку М, которая доставила бы минимум функции R₁(k,x₀) (рис.2). Из рисунка видно, что обычный экстремум (в данном случае-минимум) для функции R₁(k,x₀) будет расположен на оси R в точке R_0,аусловных- в точке М₁. Решение проведем методом множителей Лагранжа. Запишем функции в принятых в цитируемом источнике обозначениях:

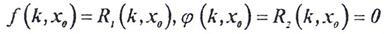
Для того, чтобы найти точки, которые могут быт точками условного экстремума функции f(k,x₀), при уравнении связи φ(k,x₀) нужно образовать вспомогательную функцию:

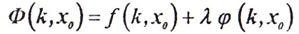
где λ — некоторая постоянная (множитель Лагранжа), и составить уравнение для отыскания точек экстремумов этой функции с учетом уравнения связи. В результате получим три уравнения для определения трех неизвестных

k, x₀ и λ:

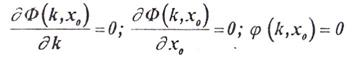
В развернутом виде эти уравнения запишутся так:

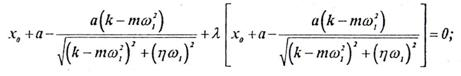
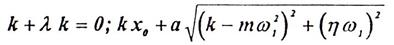
Из второго уравнения будем иметь (k≠0) λ=-1,а из первого (после подстановки значения λ) — k= ω₁².

Имя значение k и подставляя его в последнее уравнение, получим:

По физическому смыслу предварительная деформация x₀ должна быт больше нуля. Если η= mω_1, то x₀=0 и предварительная деформация x₀ упругого элемента не нужно. Отбрасывая на основании этого в уравнении связи слагаемое, содержащее x₀ получим единственное выражение для подсчета k;

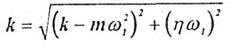
Отсюда будем иметь:

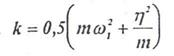
Из проведенного решения следует, что предварительная деформация x₀ упругого элемента нужно только в случае достаточно большого сопротивления движению механизма, характеризуемого коэффициентом η. Например, если η= mω_1, то k= mω_1. Граничное значение η= mω₁ указывает на то, что, хотя при этом x₀=0, жесткость k упругого элемента должна подсчитываться по формуле k= mω₁²_.

Литература:

1.                  Лебедев В. С. Технологические процессы машин и аппаратов в производствах бытового обслуживания. -М.: Легпромбытиздат, 1991. -331 с.

2.                  Макаров А. И., Крылов В. В. и др. Расчет и конструирование машин прядильного производства. -М.: Машиностроение, 1981. — 464 с.

3.                  Маракушев Е. А. и др., Машины швейного производства. Конструкция, расчет и основы проектирования. –Киев, Техника, 1967. — 324 с.