Несмотря на существование различных исследований и работ по изучению качения колеса и его взаимодействия с твердой опорной поверхностью, известно малое число исследований, в которых рассматриваются общие вопросы теории качения деформируемого (эластичного) колеса. При этом в части исследований рассматривается качение колеса с учетом сил, действующих только в его срединной плоскости, другие — только действие боковых сил, третьи исследуют стационарное движение, четвертые нестационарное, применяя к нему результаты, полученные в стационарном случае, не оценивая при этом границы применимости своих исследований.
Таким образом, в изучении качения эластичного колеса отсутствует единая теория, содержатся противоречивые мнения, а также множество экспериментальных работ имеют абсолютно разный характер, что приводит к трудности нахождения основы, на которую они полагаются. [1]
Колесо имеет достаточно долгую историю развития. С началом применения колеса для перемещения каких-либо объектов оно совершенствовалось и прошло путь начиная от жесткого обода со спицами до эластичного колеса. В свою очередь, помимо преимуществ относительно жесткого обода, использование эластичного колеса привело к появлению различных явлений, таких как колебания колес, приводивших к потере управляемости.
Постепенно, ученые все больше исследовали теорию качения колеса, пытаясь определить силы, действующие в зоне контакта колеса с опорной поверхностью, учитывая при этом параметры его движения.
Итак, теория качения стала неотъемлемой частью исследований движения колесного транспорта и стала иметь большее значение при проектирование новых машин. При этом было необходимо описать динамические явления движения, что повлияло на затяжное развитие теории качения колеса.
При решении статических задач по определению нормальных (вертикальных) реакций на горизонтальной поверхности при неподвижной оси колеса известно, что точка приложения вертикальной реакции располагается в центре пятна контакта.
По вопросу стационарного качения имеется большое число публикаций. Особый интерес представляют исследования А. Ю. Ишлинского в связи с наиболее ранней и эффективной реализацией в них модельного подхода. Стоит отметить работы таких авторов как Д. А. Антонова, В. Л. Бидермана, Н. Ф. Бочарова, Ю. А. Ечистова, В. А. Илларионова, Н. К. Куликова, В. И. Новопольского, Ю. В. Пирковского, А. Булла, Ф. Бема, А. Франка, Р. Эванса, Н. И. Глаголева, В. П. Горячкина, И. И. Калкера, В. И. Кнороза, А. С. Литвинова, О. Н. Мухина, В. А. Петрушова, Е. А. Чудакова, Е. Фиала, Г. Фромма, Р. Хадекеля, Р. Смайли и В. Хорна, Д. Нордин и др.
Исследования качения колеса в ведомом режиме хорошо известны и их результатами является утверждение, что вертикальная реакция в этом случае смещена в сторону движения на величину ![]() , где
, где ![]() — коэффициент сопротивления качению;
— коэффициент сопротивления качению; ![]() — динамический радиус колеса [2–5]. Причиной возникновения смещения является необходимость преодоления различных потерь энергии как непосредственно в зоне контакта, так и в самом материале колеса, участки которого при качении колеса подвергаются постоянно периодически меняющимся по направлению деформациям. Более поздние исследования показали, что картина смещения точки приложения вертикальной составляющей реакции определяется не только потерями в зоне пятна контакта и в материале колеса, но и упругими связями колеса, из-за чего положение оси колеса оказывается не неизменным в продольном направлении, а зависит от величины продольных сил [6].
— динамический радиус колеса [2–5]. Причиной возникновения смещения является необходимость преодоления различных потерь энергии как непосредственно в зоне контакта, так и в самом материале колеса, участки которого при качении колеса подвергаются постоянно периодически меняющимся по направлению деформациям. Более поздние исследования показали, что картина смещения точки приложения вертикальной составляющей реакции определяется не только потерями в зоне пятна контакта и в материале колеса, но и упругими связями колеса, из-за чего положение оси колеса оказывается не неизменным в продольном направлении, а зависит от величины продольных сил [6].
Исследователями Зотовым Н. М. и Балакиной Е. В. [7] ранее было предложено разделение общепринятого в настоящее время понятия продольного сноса нормальной реакции опорной поверхности не на две, а на три составляющих. Одна составляющая, как обычно, характеризует гистерезисные потери (радиальные и тангенциальные) на качение колеса; другая составляющая, как обычно, характеризует продольное упругое перемещение оси колеса относительно геометрического центра пятна контакта, а третья, вновь введенная составляющая, характеризует упругие угловые деформации шины, вызывающие несимметричность эпюры нормальных напряжений в зоне пятна контакта. Как выяснилось, эта новая, третья составляющая на прядок превышает две другие.
Что касается точки приложения боковой реакции, то здесь можно заметить, что для неподвижного колеса точка приложения сосредоточенной боковой реакции располагается в центре пятна контакта, так же, как и точка приложения нормальной реакции. При движении колеса, в зависимости от величины и знака момента, действующего на колесо, в зоне контакта начинают возникать участки с продольным проскальзыванием, что снижает трение покоя на этих участках, перемещая тем самым положение боковой реакции, приложенной к середине участка с трением покоя в пятне контакта.
Направление действия продольной реакции совпадает с продольной осью симметрии пятна контакта для неподвижного колеса. У катящегося колеса продольная реакция перемещается в боковом направлении на величину, определяемую по известным рекомендациям А. С. Литвинова.
На рисунке 1 представлена предлагаемая авторами классификация взаимосвязей реакций опорной поверхности на эластичное колесо и их сносов.
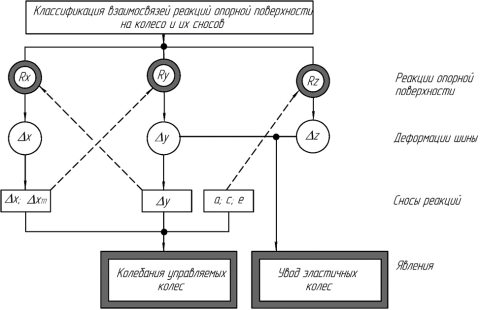
Рис. 1. Классификация взаимосвязей реакций опорной поверхности и их сносов
Три реакции опорной поверхности ![]() ,
, ![]() ,
, ![]() , действующие на эластичное колесо с шиной, вызывают по соответствующим направлениям упругие деформации шины:
, действующие на эластичное колесо с шиной, вызывают по соответствующим направлениям упругие деформации шины: ![]() ,
, ![]() ,
, ![]() .
.
Продольная деформация шины ![]() определяется продольными упругими свойствами шины:
определяется продольными упругими свойствами шины:
![]() ,
,
где ![]() — продольная реакция опорной поверхности;
— продольная реакция опорной поверхности; ![]() — коэффициент продольной жесткости шины.
— коэффициент продольной жесткости шины.
Боковая деформация шины ![]() определяется боковыми упругими свойствами шины:
определяется боковыми упругими свойствами шины:
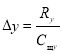 ,
,
где ![]() — боковая реакция опорной поверхности;
— боковая реакция опорной поверхности; ![]() — коэффициент боковой жесткости шины.
— коэффициент боковой жесткости шины.
Нормальная (радиальная) деформация шины ![]() определяется радиальными упругими свойствами шины:
определяется радиальными упругими свойствами шины:
![]() ,
,
где ![]() — нормальная (вертикальная) реакция опорной поверхности;
— нормальная (вертикальная) реакция опорной поверхности; ![]() — коэффициент нормальной (радиальной) жесткости шины.
— коэффициент нормальной (радиальной) жесткости шины.
Эти упругие деформации вызывают некоторые сносы ![]() ,
, ![]() ,
, ![]() реакций опорной поверхности по соответствующим направлениям.
реакций опорной поверхности по соответствующим направлениям.
Продольная упругая деформация ![]() является частью продольного сноса для боковой реакции
является частью продольного сноса для боковой реакции ![]() . Другая часть продольного сноса боковой реакции определяется взаимным расположением зон разного трения в пятне контакта. Как показывают исследования напряжений в пятне контакта,
. Другая часть продольного сноса боковой реакции определяется взаимным расположением зон разного трения в пятне контакта. Как показывают исследования напряжений в пятне контакта,
![]() ,
,
где ![]() — длина пятна контакта;
— длина пятна контакта; ![]() — величина продольного сноса боковой реакции опорной поверхности, обусловленная продольным смещением участка с трением покоя в пятне контакта.
— величина продольного сноса боковой реакции опорной поверхности, обусловленная продольным смещением участка с трением покоя в пятне контакта.
Продольный снос боковой реакции влияет на параметры колебаний управляемых колес вокруг осей поворота, поскольку изменяет плечо силы ![]() .
.
Боковая деформация ![]() является боковым сносом для продольной реакции
является боковым сносом для продольной реакции ![]() и влияет на параметры колебаний управляемых колес вокруг осей поворота, поскольку изменяет плечо силы
и влияет на параметры колебаний управляемых колес вокруг осей поворота, поскольку изменяет плечо силы ![]() (плечо обкатки). Также боковая деформация
(плечо обкатки). Также боковая деформация ![]() является боковым сносом для нормальной реакции
является боковым сносом для нормальной реакции ![]() , но это не влияет на явления в пятне контакта, поэтому на схеме рисунка 1 эта связь не показана.
, но это не влияет на явления в пятне контакта, поэтому на схеме рисунка 1 эта связь не показана.
Радиальная деформация ![]() не является ничьим сносом, но она определяет длину пятна контакта и вместе с деформацией
не является ничьим сносом, но она определяет длину пятна контакта и вместе с деформацией ![]() определяют параметры явления увода эластичного колеса.
определяют параметры явления увода эластичного колеса.
Продольный снос реакции ![]() , который, как было сказано, включает три составляющие
, который, как было сказано, включает три составляющие ![]() , влияет на параметры колебаний управляемых колес вокруг осей поворота, поскольку изменяет плечо силы
, влияет на параметры колебаний управляемых колес вокруг осей поворота, поскольку изменяет плечо силы ![]() .
.
Деформация шины ![]() , представляет собой снос
, представляет собой снос ![]() реакции
реакции ![]() , является плечом силы
, является плечом силы ![]() и обеспечивает момент в пятне контакта
и обеспечивает момент в пятне контакта ![]() , влияющий на колебания управляемых колес. С другой стороны,
, влияющий на колебания управляемых колес. С другой стороны, ![]() , вместе с радиальной деформацией шины
, вместе с радиальной деформацией шины ![]() (обеспечивается
(обеспечивается ![]() ), определяют увод эластичного колеса автомобиля. Иное дело обстоит с деформацией шины
), определяют увод эластичного колеса автомобиля. Иное дело обстоит с деформацией шины ![]() , которая представляет собой соответственно снос боковой реакции
, которая представляет собой соответственно снос боковой реакции ![]() . Влияние
. Влияние ![]() на траекторию автомобиля непрозрачно и обеспечивается через ряд моментов в пятне контакта, при этом это влияние происходит совместно с влиянием
на траекторию автомобиля непрозрачно и обеспечивается через ряд моментов в пятне контакта, при этом это влияние происходит совместно с влиянием ![]() .
.
При математическом моделировании траектории движения транспортных средств с эластичными колесами по твердой поверхности необходимо определять значения реакций в пятне контакта каждого колеса со стороны дороги и мест их приложения. Потребность определения точек приложения реакций в пятне контакта вызвана необходимостью моделирования движения колеса и различных явлений в пятне контакта, определяющих параметры движения автомобиля. Такое моделирование, в частности, необходимо при анализе устойчивости движения автомобиля, так как определяет явления угловых колебаний управляемых колес и увода.
Литература:
1. Левин М. А., Фуфаев Н. А. Теория качения деформируемого колеса. — М.: Наука. Гл. ред. физ.-мат. лит., 1989. — 272 с.
2. Балакина Е. В. Устойчивость движения колесных машин / Е. В. Балакина, Н. М. Зотов. — Волгоград: РПК «Политехник», 2011. — 464 с.
3. Балакина Е. В. Определение взаимного расположения сил, реак¬ций и зон трения в пятне контакта эластичного колеса с твердой по¬верхностью / Е. В. Балакина, Н. М. Зотов // Трение и износ. — 2015. — т.36, № 1. — C. 36–40.
4. Кравец, В. Н. Теория автомобиля. Учебник для вузов / В. Н. Кравец, В. В. Селифонов. — М.: ООО «Гринлайт», 2011. — 884 с.
5. Ларин, В. В. Теория Движения полноприводных колесных ма¬шин. — М.: Изд-во МГТУ им. Н. Э. Баумана, 2010. — 392 с.
- Петрушов, В. А. Автомобили и автопоезда: Новые технологии исследования сопротивлений качения и воздуха. — М.: ТОРУС ПРЕСС, 2008. — 352 с.
7. Патент № 2539847 Российская Федерация, МПК G01L 5/16, G01M 17/013. Способ определения силовых факторов, действующих на колесо транспортного средства / Балакина Е. В., Зотов Н. М., Зотов В. М., Федин А. П.; заявитель и патентообладатель Волгоградский ГТУ; заявл. 04.07.2013. — № 2013130710/28; опубл. 27.01.15 // Изобретения. Полез-ные модели. — 2015. — Бюл. № 3.

