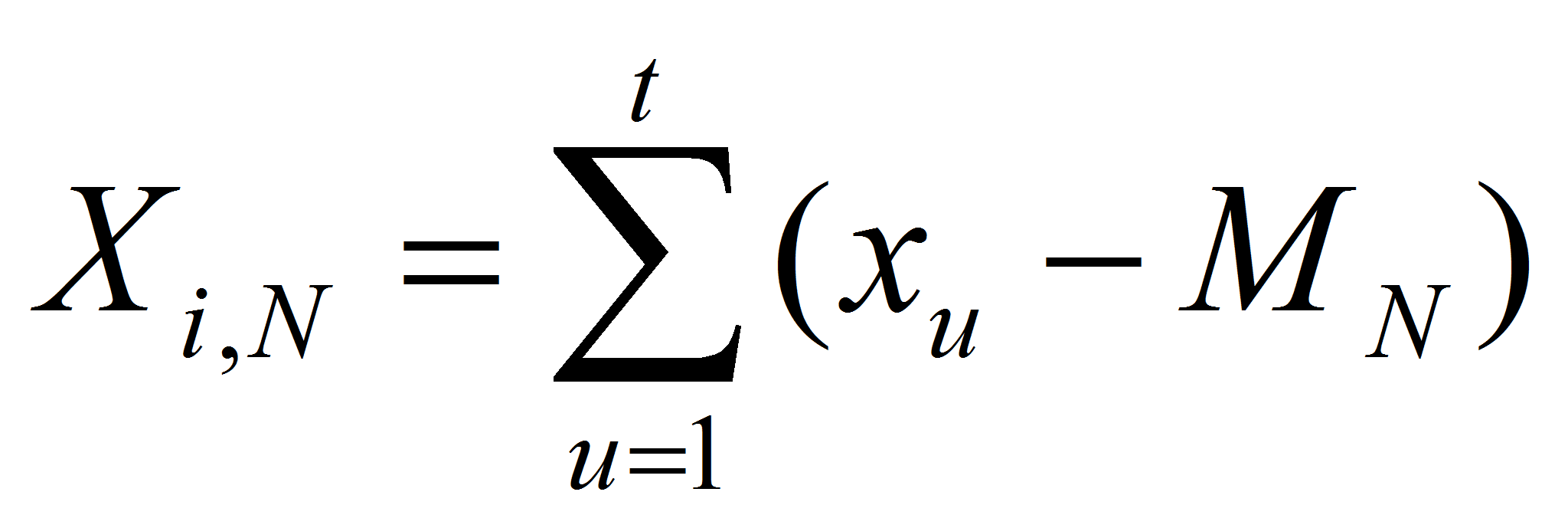Данная работа посвящена исследованию фрактальных свойств профиля шероховатости поверхностей, обрабатываемых выглаживанием с жестким закреплением индентора. В статье изложены результаты разработки метода определения фрактальной размерности посредством вычисления нормированного размаха и приведены результаты анализа профилограмм.
Шероховатость обработанной поверхности является одним из важнейших факторов, которые определяют качество обработки и оказывают влияние на эксплуатационные свойства деталей и узлов. Профиль шероховатости поверхности имеет сложную структуру и до сих пор не создано системы параметров, которые бы в полной степени отражали его строение и свойства. Данная проблема усугубляется в том случае, когда возникает необходимость построения математической модели профиля шероховатости поверхности.
Эффективным решением может являться использование аппарата фрактальной геометрии, который позволяет выявлять структурные особенности объектов с различной природой. Одним из центральных понятий фрактальной геометрии является размерность, которая является мерой самоподобия объекта. Существует несколько методов определения данной величины [1,4,5]: определение фрактальной размерности геометрическим методом, при помощи спектра мощности, методом нормированного размаха, методом максимумов модулей вейвлет-преобразования. В работах [3,6] на примере анализа фрактальной размерности профилей поверхностей, обработанных точением, было установлено, что наибольшей точности определения фрактальной размерности можно добиться при использовании метода нормированного размаха. В работах [2,3] было показано, что профили шероховатости при точении и выглаживании имеют схожую структуру, поэтому для анализа профилограмм выглаженных поверхностей также будем использовать данный метод.
Суть метода определения фрактальной размерности методом нормированного размаха состоит в следующем:
1. Вычисляются отклонения от среднего значения:
где u – длина периода, которая варьируется от 3 до N; N – длина временного ряда; t – переменная, меняющая свое значение от 1 до N-1; xu – конкретный элемент временного ряда; MN – среднее значение N элементов временного ряда.
2. На каждой итерации
получается N-1 значений
![]() ,
которые используются для определения размаха:
,
которые используются для определения размаха:
3. Производится нормирование размаха посредством деления его на стандартное отклонение N значений временного ряда:
Стандартное отклонение вычисляется по N значениям временного ряда:
4. Логарифмируются значения R/S и N и строится график функции:
5. По графику функции определяется угол наклона путем линейной аппроксимации методом наименьших квадратов. Тангенс этого угла и является показателем Херста.
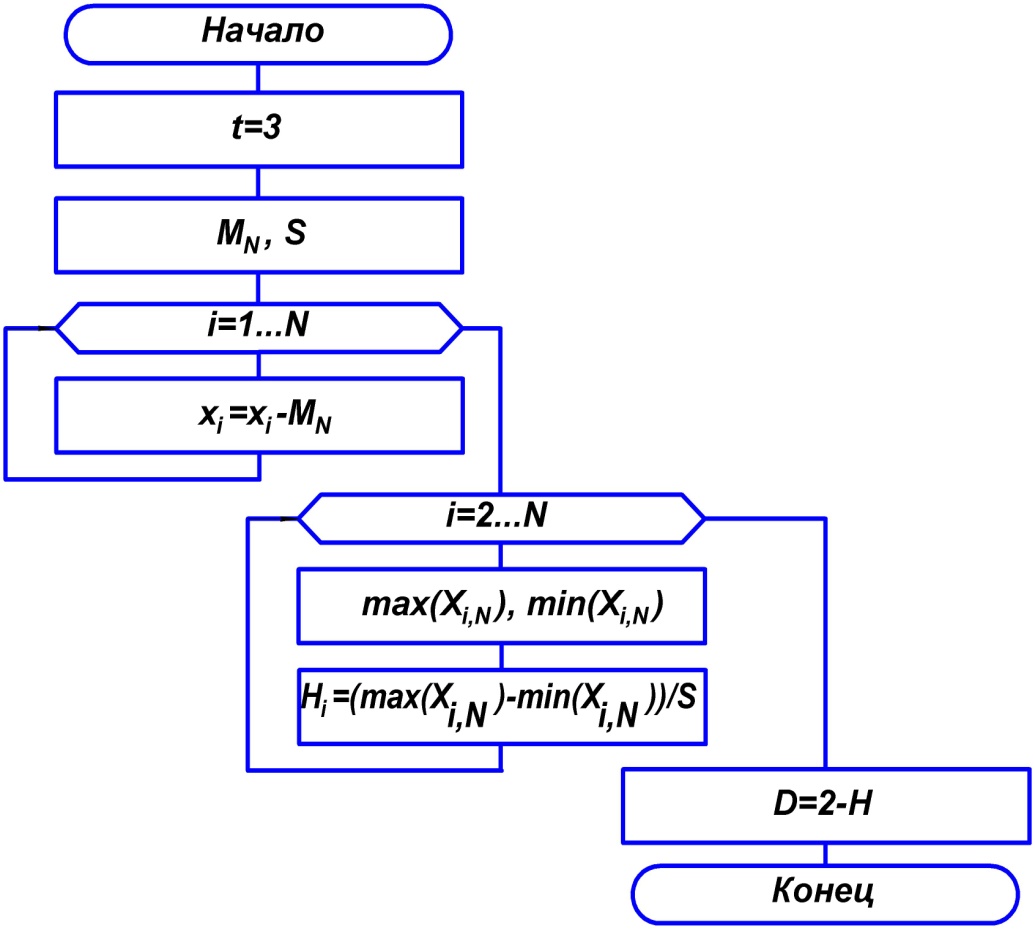
Графически алгоритм определения показателя Херста представлен на рис. 1:
Рис. 1. Алгоритм определения показателя Херста
Данный алгоритм был реализован в программной среде Borland Delphi 7.0, в которой была написана компьютерная программа «Определение фрактальной размерности временного ряда при помощи показателя Херста v1.0» [7].
Результат вычисления фрактальной размерности представлен на рис. 2:
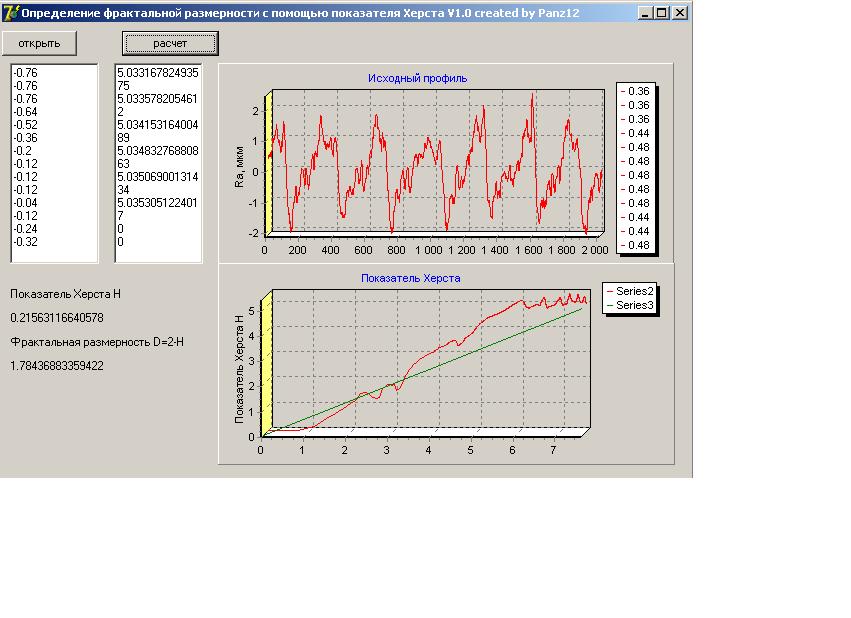
Рис.
2. Определение фрактальной размерности при помощи показателя Херста
Зависимость фрактальной размерности D от показателя Херста H имеет следующий вид:
где
![]() - Евклидова (топологическая) размерность объекта.
- Евклидова (топологическая) размерность объекта.
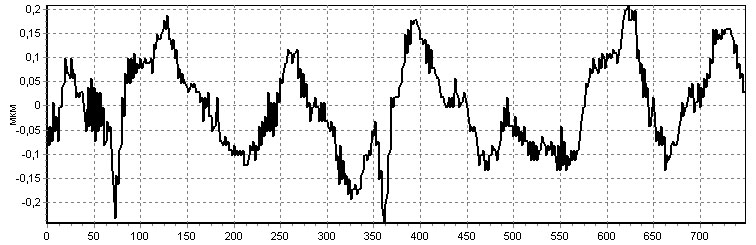
При помощи разработанного программного обеспечения было проанализировано более 200 профилограмм поверхностей, обработанных выглаживанием с жестким закреплением индектора, пример профилограммы приведен на рис. 3:
Рис. 3. Профилограмма выглаженной поверхности
В результате вычислений и последующего анализа результатов было установлено, что величина фрактальной размерности лежит в пределах DH=1.6…1.8, что говорит о существенной изрезанности профиля выглаженной поверхности. Кроме того, проведенные исследования показали, что корреляция между величиной фрактальной размерности и параметрами шероховатости по ГОСТ 2789-83 (Ra, Rz, Rmax и т.д.) лежит в пределах 0.75…0.9.
Заключение. Проведенные исследования показали, что величину фрактальной размерности можно использовать в качестве характеристики шероховатости поверхности, т.к. коэффициент корреляции между ней и параметрами по ГОСТ 2789-83 превышает 0.7, и данная величина более адекватно отражает изменения в структуре профиля, т.к. она связана со степенью его изрезанности.
Литература:
1. Кроновер Р.М. Фракталы и Хаос в динамических системах: Основы теории. - М.: Постмаркет, 2000.-352 с.
2. Овсянников В.Е., Губанов В.Ф. Марфицын В.В. Инновации при выглаживании с жестким закреплением индентора: Монография. - Lambert academic publishing, Germany, Saabrucken, 2012. – 224 c.
3. Овсянников В.Е., Остапчук А.К. Научные основы обеспечения шероховатости поверхности на базе анализа случайных процессов: монография. - Курган, изд-во Курганского гос. ун-та, 2012. – 252 с.
4. Овсянников В.Е., Симонов А.М., Остапчук А.К. Основы обеспечения качества поверхности деталей машин с использованием динамического мониторинга: монография. Курган: Изд-во Курганского гос. ун-та,2010.- 118 с.
5. Овсянников В.Е., Остапчук А.К. Применение теории фракталов в математическом моделировании и технике: учебное пособие. – Курган Изд-во Курганского гос. ун-та, 2009. - 64 с.
6. Овсянников В.Е., Остапчук А.К. Управление формированием шероховатости поверхности при обработке на токарных станках с ЧПУ: монография. - Lambert academic publishing, Germany, Saabrucken, 2011. – 218 c.
7. «Определение фрактальной размерности временного ряда при помощи показателя Херста v1.0»: свидетельство об отраслевой регистрации разработки №11373 / А.К. Остапчук, В.Е. Овсянников, Е.Ю. Рогов. - № 50200801858; заявл. 11.09.2008; опубл. 11.09.2008; Инновации в науке и образовании №9(44). 6 с.