Использование мощных энергетических установок не только на производстве, но и на всех видах транспорта неизбежно приводит к возникновению вибрации. Вибрация отрицательно влияет на надежность, долговечность самих машин, на сооружения, аппараты, в которых они установлены, а также на системы автоматического управления. Не редкость, что вибрация является одной из причин аварий. Наиболее остро проблема виброзащиты стоит в автомобилестроении, судостроении, где в качестве энергетических установок используются двигатели внутреннего сгорания (ДВС). Низкочастотные колебания, создаваемые ДВС, наиболее вредны для человека, вызывая различные заболевания. Поэтому на сегодняшний день борьба с механическими колебаниями (вибрацией) является одной из важнейших задач.
Существует множество способов уменьшения вибрации – это динамическое уравновешивание двигателей, применение динамических гасителей колебаний, активные виброзащитные системы с дополнительным источником вибрации и т.д. Наибольшее распространение получила виброизоляция, выполняемая в виде резинометаллических амортизаторов. Однако, отличаясь простотой и надёжностью, такие виброизоляторы малоэффективны, так как снижение их коэффициента жёсткости с целью уменьшения передаваемых динамических усилий, приводит к увеличению относительных перемещений ДВС и сочленяемого с двигателем оборудования. Этого недостатка лишены виброизоляторы с «плавающим» участком нулевой жёсткости. Применение виброизолирующих устройств с плавающим участком нулевой жёсткости [1] является наиболее перспективным методом снижения уровней вибрации. В таких виброизоляторах параллельно упругим элементам включены перестраивающиеся компенсаторы жёсткости, имеющие падающую силовую характеристику (отрицательный коэффициент жёсткости). На сегодняшний день разработано большое количество конструкций компенсаторов, однако они не отвечают современным требованиям виброизоляции. Из известных наиболее эффективным следует считать электромагнитный компенсатор жёсткости (ЭКЖ) [2], так как он наиболее полно отвечает требованиям идеальной виброизоляции как при постоянных по величине, так и при произвольно меняющихся нагрузках. Конструктивно ЭКЖ - два встречно включенных электромагнита, обеспечивающих устройству падающую силовую характеристику, что позволяет корректировать жёсткость виброизолятора в целом. Для нормального функционирования виброизолирующей подвески с коррекцией жёсткости при изменяющихся внешних нагрузках, компенсатор снабжен специальной системой перестройки. Для обеспечения плавания участка нулевой жёсткости при изменении усилий система перестройки перераспределяет напряжение на катушках электромагнитов. В [3] установлено, что закон изменения напряжения на электромагнитах при изменении перемещения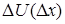 
может быть: линейным и нелинейным, как показано на рисунках 1, 2. В [4] показано, что нелинейный закон изменения напряжения на катушках электромагнитов может быть аппроксимирован квадратичной зависимостью:
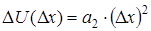, (1)
где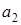 
- постоянный коэффициент.
Перейдем от переменным в (1) к переменным: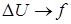 
, 
:
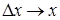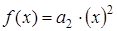. (2)
где f(x) – исходная непрерывная функция;
x – независимая переменная.
Исследование виброизолирующей системы в обоих случаях системы перестройки показало, что наиболее предпочтительным является применение линейной системы перестройки. К тому же практически реализовать линейный вариант регулятора значительно проще. Поэтому попытаемся перейти от квадратично аппроксимированного нелинейного закона зависимости напряжения от относительного перемещения вибрирующего и защищаемого объектов к линейному закону. Так как виброизолирующая система работает при достаточно малых относительных перемещения вибрирующего и защищаемого объектов, то рассмотрим нелинейный закон, изображенный на рисунке 2 на отрезке [a, b] близким к началу координат. Выполнив ряд расчетов нелинейного закона изменения напряжения от изменения перемещения на заданном отрезке, можно заметить, что зависимость описывается уравнением (2), но при этом коэффициент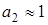 
. То есть нелинейная закон на отрезке [a, b] описывается уравнением
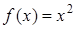. (3)
.
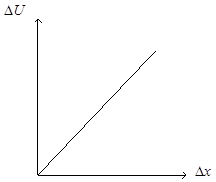
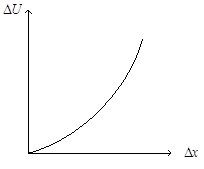
Теперь попробуем выполнить приближение получить линейную зависимость, воспользовавшись теоремой Вейерштрасса [5]: если функция f(x) непрерывна на отрезке [a, b], то, как было мало ни было положительное число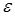 
, найдется полином 
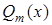достаточно высокой степени m, абсолютное отклонение которого от данной функции f(x) на отрезке [a, b] меньше, чем 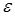, то есть для всех точек 
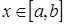имеет место неравенство
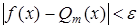(4)
где 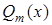- непрерывный аппроксимирующий обобщенный полином;
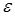- квадратичное отклонение (отклонение от нуля).
Для функции (3) полиномом наилучшего приближения
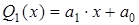(5)
где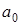 
, 
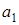- постоянные коэффициенты,
первой степени на отрезке [a, b] является
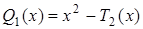, (6)
где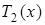 
- полином Чебышева.
Действительно, согласно смыслу задачи разность
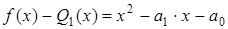. (7)
есть полином наилучшего приближения, наименее уклоняющийся от нуля на заданном отрезке, то есть представляет собой полином Чебышева.
Необходимо определить коэффициенты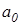 
и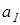 
так, чтобы величина 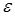, согласно (4), была наименьшей.
Следовательно, полином
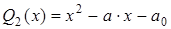(8)
наименее отклоняется от нуля на отрезке [a, b].
Необходимые коэффициенты в уравнении полинома (8) можно рассчитать из следующего выражения:
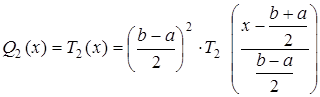. (9)
Подставив уравнение (8) с полученными коэффициентами в выражение (6), получим
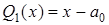. (10)
Перейдём к переменным, действующим в системе перестройки компенсатора, то есть к приращению напряжения ΔU и приращению перемещения Δх:
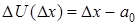. (11)
Характеристика, приближенно описывающая зависимость изменения напряжения от изменения перемещения, приведена на рисунке 3 (график 2). Из рисунка 3 видно, что на отрезке [a, b] характеристику можно описать уравнением (11), то есть полином первой степени с наименьшими отклонениями от заданной кривой (график 1), полученной в [4]. Следовательно, зависимость изменения напряжения на одном электромагните от изменения перемещения на отрезке [a, b] можно рассматривать прямолинейной. Причем отклонение от нуля можно рассчитать по выражению:
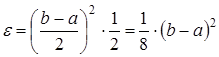. (12)
Заметим, что отклонение 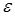реализуется в трех точках:
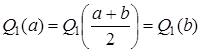. (13)
Из рисунка 3, видно геометрически график функции (11) представляет собой среднюю параллель между секущей, проходящей через крайние точки, и касательной, параллельной этой секущей.
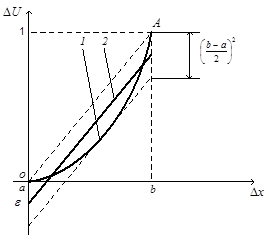
Рисунок 3 – Зависимости изменения напряжения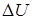 
на электромагните от
изменения перемещения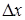 
: 1 – точная кривая; 2 – аппроксимированная кривая
Полученную зависимость изменения напряжения на электромагните достаточно просто использовать при математическом моделировании виброизолятора и для практической реализации системы перестройки.
Литература
1 Зуев, А. К. Основные положения теории виброизоляции произвольных пространственных колебаний [Текст] / А. К. Зуев // Снижение вибрации на судах : сб. науч. тр. / Новосиб. ин-т инженеров вод. трансп. – Новосибирск, 1991. – С. 4 – 17.
2 Гросс, В. Ю. Электромагнитный компенсатор жёсткости [Текст] / В.Ю. Гросс, В.А. Чирков, А.Ю. Крылов // Виброизоляция судовых силовых установок : сб. науч. тр. / Новосиб. ин-т инженеров вод. трансп. – Новосибирск, 1985. – С. 31 – 34.
3 Гурова, Е. Г. Виброизолирующая подвеска судовой энергетической установки с нелинейным электромагнитным компенсатором жёсткости [Текст] : автореферат дис. канд. техн. наук / Гурова Елена Геннадьевна. – Новосибирск, 2008. – 22 с.
4 Гурова, Е. Г. К описанию системы перестройки электромагнитного компенсатора жёсткости [Текст] / Е.Г. Гурова, В.Ю. Гросс // Научные проблемы транспорта Сибири и Дальнего Востока : сб. науч. тр. / Новосиб. гос. акад. вод. трансп. – Новосибирск, 2008. – №2. – С. 250– 253.
5 Пискунов, Н. С. Дифференциальное и интегральное исчисление [Текст] : / Н.С. Пискунов; под ред. И.В. Кеппена. –М. : ФИЗМАТГИЗ, 1963. –851 с.
