Описание движения элемента конструкции, в частности, балочной конструкции, в процессе ее деформирования динамической нагрузкой с целью нахождения условий его гарантированного разрушения представляет собой довольно сложную задачу. Затруднения возникают в связи с необходимостью учитывать возникновение и движение пластических участков (пластических зон) переменной длины (конструкции), колебательный характер упругих участков деформируемого элемента, взаимное влияние нагрузки на деформируемый элемент и элемента на действующую динамическую нагрузку. Кроме того, описание указанного процесса деформирования приводит к сложной системе нелинейных дифференциальных уравнений в частных производных.
Однако, решение может быть найдено по другому пути, используя следующие соображения. Гарантированные разрушение элемента конструкции (возникновение в нем трещины или пластических зон, или разделения на фрагменты) с большой вероятностью получим в самой начальной стадии деформирования, когда нагрузка максимальна и, следовательно, воздействуя на элемент конструкции, сообщает ему максимально возможную кинетическую энергию, которая впоследствии расходуется на работу деформирования (разрушения) этого элемента. Так возникла идея энергетического метода исследования процесса разрушения элементов конструкций динамической нагрузкой [1].
Идея метода. Постановка задачи. Основные соотношения. Идея этого метода сводится к использованию закона сохранения энергии, а именно: кинетическая энергия, полученная балкой в результате действия на нее взрыва заряда, приравнивается к работе деформирования балки.
Требуется: для свободно стертой по концам балки, длиной l, постоянного поперечного сечения, подверженной действию импульсной динамической нагрузки, созданной взрывом сосредоточенного заряда над серединой пролета балки, используя энергетический метод, найти приближенно начальную форму упругой линии, необходимую в дальнейшем для отыскания условий гарантированного разрушения (гарантированной взрывостойкости) балочной конструкции.
В частном случае взрыва сосредоточенного сферического заряда над серединой пролета балки на расстоянии а от нее кинетическая энергия может быть вычислена наиболее просто, если начало координат совместить с серединой балки. Тогда при относительных расстояниях 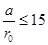 удельный импульс, действующий на балку, вычисляется по формуле [1]:
удельный импульс, действующий на балку, вычисляется по формуле [1]: 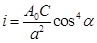
Начальная скорость балки в сечении х :
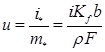 (1)
(1)
где 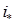 - погонный (отнесенный к единице длины) импульс,
- погонный (отнесенный к единице длины) импульс, 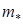 - погонная масса балки,
- погонная масса балки, 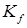 - коэффициент формы, учитывающий расположения балки по отношению к действующей импульсной нагрузки, b – ширина балки,
- коэффициент формы, учитывающий расположения балки по отношению к действующей импульсной нагрузки, b – ширина балки, 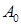 - константа, определяющая вид заряда взрывчатого вещества, C – масса заряда,
- константа, определяющая вид заряда взрывчатого вещества, C – масса заряда, 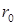 - радиус заряда,
- радиус заряда, 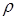 - плотность взрывчатого вещества, F – площадь поперечного сечения балки, i – импульс, создаваемый взрывной нагрузкой, u – скорость элемента.
- плотность взрывчатого вещества, F – площадь поперечного сечения балки, i – импульс, создаваемый взрывной нагрузкой, u – скорость элемента.
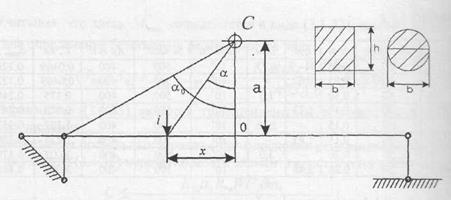
Рис.1. Схема для определения кинетической энергии балки
Кинетическая энергия элемента балки
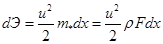 (2)
(2)
Учитывая, что 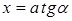 и соотношение (1), выражение (2) запишем в виде
и соотношение (1), выражение (2) запишем в виде
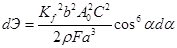 (3)
(3)
Кинетическая энергия, полученная балкой
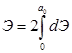 (4)
(4)
где 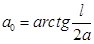
Подставив выражение (3) в формулу (4) и вводя обозначение:
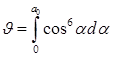
получим 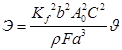
Для балки прямоугольного поперечного сечения с параметрами 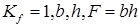
Кинетическая энергия имеет вид: 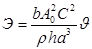
Для балки круглого поперечного сечения: 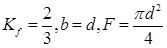
получим 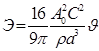
Вычислим теперь работу деформирования балки. Элементарная работа деформирования 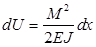 ,
,
где изгибающий момент вычисляется в виде: 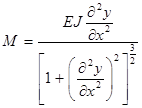
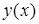 - прогиб балки в сечении x, l – длина балки.
- прогиб балки в сечении x, l – длина балки.
Следовательно, 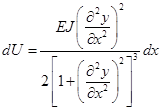
В силу симметрии, работа деформирования балки: 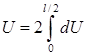
т.е. 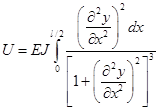 (5)
(5)
Из выражения (5) видно, что для того, чтобы найти работу деформирования балки нужно знать форму ее упругой линии.
Согласно методу аппроксимации Галёркина-Бубнова, зададим форму упругой линии так, чтобы удовлетворялись граничные условия для балки.
Для свободно опертой балки и начала координат, совпадающим с серединой пролета балки, граничные условия имеют вид:
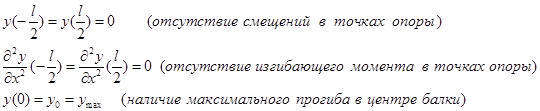 (6)
(6)
Метод Ритца. Идея метода Ритца заключается в том, что значения некоторого функционала I[y(x)] рассматриваются не на произвольных допустимых кривых данной вариационной задачи, а лишь на всевозможных линейных комбинациях 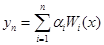 с постоянными коэффициентами, составленных из n первых функций некоторой выбранной последовательности функций:
с постоянными коэффициентами, составленных из n первых функций некоторой выбранной последовательности функций:
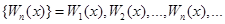
Функции 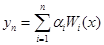 должны быть допустимыми в рассматриваемой задаче, что налагает ограничения (6) на выбор последовательности функций
должны быть допустимыми в рассматриваемой задаче, что налагает ограничения (6) на выбор последовательности функций 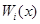 . На таких линейных комбинациях функционал I[y(x)] превращается в функцию
. На таких линейных комбинациях функционал I[y(x)] превращается в функцию 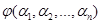 коэффициентов
коэффициентов 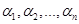 . Эти коэффициенты
. Эти коэффициенты 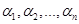 выбираются так, чтобы функция
выбираются так, чтобы функция 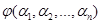 достигала экстремума; следовательно,
достигала экстремума; следовательно, 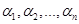 должны быть определено из системы уравнений:
должны быть определено из системы уравнений:
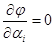 , i=1,2,…,n
, i=1,2,…,n
Совершая предельный переход при 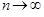 , получим (в случае существования предела) функцию
, получим (в случае существования предела) функцию 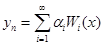 , являющуюся точным решением рассматриваемой вариационной задачи. Если не совершать предельного перехода, а ограничиться лишь п первыми членами
, являющуюся точным решением рассматриваемой вариационной задачи. Если не совершать предельного перехода, а ограничиться лишь п первыми членами 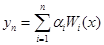 , то получим приближенное решение.
, то получим приближенное решение.
Решение задачи. Поставим задачу: используя метод Ритца найти функцию y(x), доставляющий минимум функционалу:
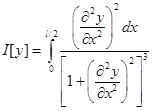 (7)
(7)
Функция y(x) должна удовлетворять граничным условиям:
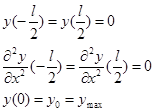 (8)
(8)
Этим граничным условиям можно удовлетворить, если задать форму упругой линии в виде:
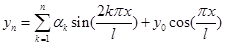 (9)
(9)
Ограничимся n=2
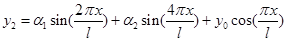 (10)
(10)
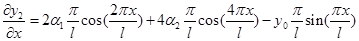
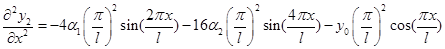
Для малых прогибов 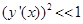 , поэтому исходный функционал (7) примет вид (11)
, поэтому исходный функционал (7) примет вид (11)
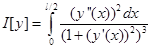
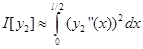 (11)
(11)
Используя программу, найдем 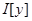 :
:
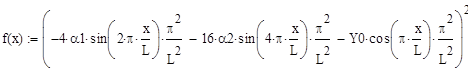

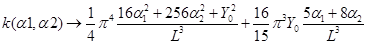
Значит: 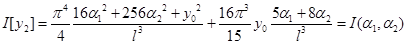
Поэтому: 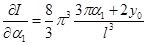
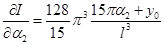
Коэффициенты 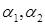 выбираются так, чтобы
выбираются так, чтобы 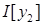 достигал минимума. Поэтому
достигал минимума. Поэтому 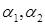 должны быть определено из системы уравнений:
должны быть определено из системы уравнений:
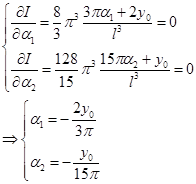
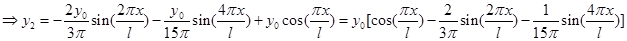 Найденная функция
Найденная функция 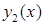 приближенно определяет начальную форму упругой линии в момент, когда балки, исчерпав весь запас кинетической энергии, полученной ей от взрывной импульсной нагрузки, на мгновение остановилась. В следующий момент накопленная балкой упругая энергия высвобождается, сообщая элементам балки определенные скорости (балка получает запас кинетической энергии), и т.д., т.е. совершаются упругие колебания.
приближенно определяет начальную форму упругой линии в момент, когда балки, исчерпав весь запас кинетической энергии, полученной ей от взрывной импульсной нагрузки, на мгновение остановилась. В следующий момент накопленная балкой упругая энергия высвобождается, сообщая элементам балки определенные скорости (балка получает запас кинетической энергии), и т.д., т.е. совершаются упругие колебания.
1. Володин Г.Т. Действие взрыва зарядов конденсированных ВВ в газовой и жидкой средах. Часть II. Взрывостойкость и гарантированное разрушение элементов конструкции.- Тула: «Левша», 2005.
2. Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление – M., 1969.

