Изучение реологических свойств нефти в настоящее время является важной практической задачей, ее решение позволит вычислять энергию необходимую для разрушения ее мономолекулярной структуры, а соответственно и рассчитать оптимальные режимы работы нефтеперекачивающих станций в зависимости от следующих факторов: предыстории нефти, изменения температуры окружающей среды и скорости движения нефти по трубопроводу. Под предысторией нефти понимается ее предыдущее состояние: находилась ли жидкость в состоянии покоя или в состоянии движения, прикладывалось ли к ней какое либо механическое воздействие.
Изучение влияния различных факторов на величину вязкости становится важным для высокопарафинистой нефти, так как данный вид нефти относится к ярко выраженным тиксотропным жидкостям, свойства (вязкость), которой сильно отличаются в зависимости не только от сдвиговой скорости, но и от времени приложения механического воздействия [1]. Кроме того, в застоявшемся состоянии, высокопарафинистая нефть обладает крепкой мономолекулярной структурой, и имеет высокую температуру застывания (от 29 до 350С), что в свою очередь, сильно влияет на переходные режимы в процессе пуска нефти по трубопроводу.
Для изучения реологических свойств жидкости в лабораторных условиях используются капиллярные и ротационные вискозиметры. Исследуемый лабораторный вискозиметр ротационного типа предназначен для снятия кривых течения высокопарафинистых нефтей, хотя может быть использован для снятия кривых течения различных типов жидкостей.
Как упоминалось выше, нефть относится к тиксотропной псевдопластичной жидкости, вследствие этого, для полного описания вязкости нефти необходимо производить снятие семейства характеристик (рис. 1). Для этого, при измерении вязкости, программно предусматривается проведение нескольких циклов измерения. Каждый цикл «разгон-сброс скорости» имеет длительность равную 4 минутам. Каждая из последующих снимаемых кривых течения будет располагаться ближе к предыдущей, и в идеале последние из снимаемых кривых будут совпадать, это означает, что установилось динамическое равновесие между разрушением и восстановлением мономолекулярной структуры нефти. В реальной системе снятие характеристик прекращается, когда ошибка D будет меньше некоторой заданной ошибки измерений 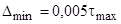 .
.
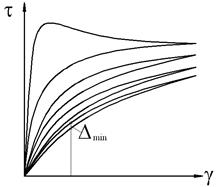
Рис. 1 Кривые течения тиксотропной псевдопластичной жидкости
Такой закон движения привода является основным, кроме этого могут быть предусмотрены дополнительные законы движения.
На рис. 2 представлена кинематическая схема привода. Для снятия кривых течения, необходимо измерять момент нагрузки на валу двигателя 1 при различных скоростях вращения измерительного зонда 3. В качестве исполнительного двигателя применяется синхронный реактивный двигатель (СРД) СОЛ-1.
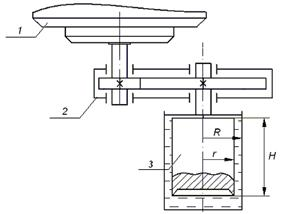
Рис. 2. Кинематическая схема привода:
1 – исполнительный двигатель; 2 – редуктор; 3 – измерительный зонд
В исследуемом вискозиметре используется косвенный способ измерения момента нагрузки за счет измерения угла нагрузки, с последующим вычислением момента. При таком способе измерения момента для получения достоверных результатов необходимо обеспечить синхронный режим работы двигателя, во всем диапазоне изменения скорости вращения зонда.
Работа синхронных реактивных двигателей в общем случае сопровождается электромеханическими переходными процессами, которые являются весьма сложными и их математическое описание не представляется возможным без применения целого ряда допущений. Поскольку СРД представляет собой частный случай явнополюсной синхронной машины, то здесь вполне закономерно применение методов исследования синхронных машин и общепринятых допущений: отсутствие насыщения магнитной цепи; отсутствие гистерезиса, потерь в стали и механических потерь; полная симметрия всех обмоток СРД; напряжение сети синусоидально и сеть обладает бесконечно большой мощностью и др.
Положительное направление продольной оси ротора d совпадает с осью полюса ротора, а ось q опережает ось d на 90 электрических градусов (рис. 3). Пусковая обмотка на роторе СРД представляется двумя эквивалентными контурами, при этом положительные токи образуются так, чтобы магнитодвижущие силы, созданные ими, совпадали с соответствующими осями d и q.
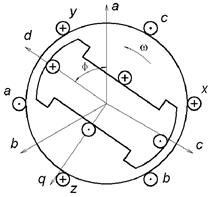
Рис. 3. Схема синхронной явнополюсной машины
В фазовой системе координат уравнения равновесия напряжений для обмоток статора и ротора записываются в виде:
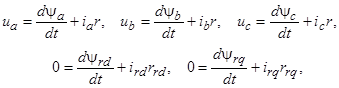 (1)
(1)
где 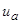 ,
,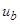 ,
, 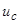 ,
, 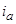 ,
, 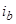 ,
, 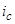 ,
, 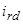 ,
, 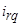 – мгновенные значения напряжения и токов в обмотках ротора;
– мгновенные значения напряжения и токов в обмотках ротора; 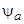 ,
, 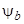 ,
,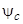 ,
, 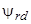 ,
, 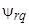 – полные потокосцепления фазных обмоток и эквивалентных роторных обмоток;
– полные потокосцепления фазных обмоток и эквивалентных роторных обмоток; 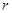 ,
, 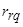 ,
, 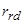 – активные сопротивления обмоток статора и эквивалентные роторных.
– активные сопротивления обмоток статора и эквивалентные роторных.
Потокосцепления обмоток в уравнениях (1) определяются выражениями:
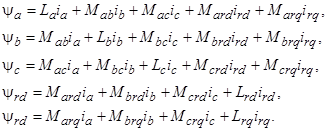 (2)
(2)
где 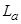 ,
, 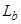 ,
,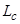 – собственные индуктивности статорных обмоток; все остальные взаимные индуктивности между соответствующими обмотками.
– собственные индуктивности статорных обмоток; все остальные взаимные индуктивности между соответствующими обмотками.
Система уравнений равновесия напряжений (1), записанная в фазовой системе координат, является системой дифференциальных уравнений с периодическими коэффициентами. Аналитического решения такие уравнения не имеют и могут быть решены лишь численными методами. Чтобы избавится от периодичности коэффициентов уравнений (1) необходимо провести линейные преобразования, связанные с преобразованием координат, например, переход к системе координат 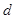 и
и 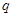 , жестко связанной с ротором. В результате:
, жестко связанной с ротором. В результате:
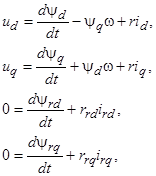 (3)
(3)
где 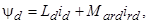
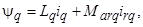
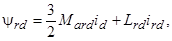
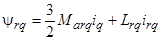 – потокосцепления;
– потокосцепления; 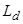 ,
, 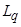 ,
, 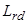 ,
, 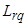 – индуктивности статорной и роторной обмоток по продольной и поперечной осям;
– индуктивности статорной и роторной обмоток по продольной и поперечной осям; 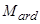 ,
, 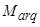 – взаимные индуктивности между обмотками статора и ротора по продольной и поперечной осям;
– взаимные индуктивности между обмотками статора и ротора по продольной и поперечной осям; 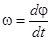 – мгновенное значение угловой скорости в электрических рад/с.
– мгновенное значение угловой скорости в электрических рад/с.
Система уравнений (3) является системой дифференциальных уравнений с постоянными коэффициентами и может быть решена аналитически. В таком виде уравнения при исследовании переходных процессов можно решить и на ЭВМ. Однако, переходя от физических величин к относительным, можно упростить исследования системы уравнений (3).
Для записи уравнений в относительных единицах, нужно выбрать базисные значения параметров, а также роторные обмотки привести к статорным, для этого необходимо определить коэффициенты приведения напряжения 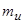 , токов
, токов 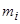 , и сопротивлений
, и сопротивлений 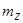 . Так, согласно [2] эти коэффициенты будут иметь вид:
. Так, согласно [2] эти коэффициенты будут иметь вид:
– коэффициенты приведения токов по продольной и поперечной осям:
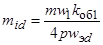 ,
, 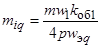 ;
;
– коэффициенты приведения напряжения по продольной и поперечной осям:
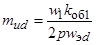 ,
, 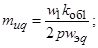
– коэффициенты приведения сопротивлений по продольной и поперечной осям: 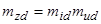 ,
, 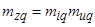 .
.
В коэффициентах: 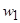 ,
, 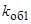 – число витков и обмоточный коэффициент фазы обмотки статора;
– число витков и обмоточный коэффициент фазы обмотки статора; 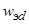 ,
, 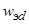 – число витков эквивалентной обмотки ротора по продольной и поперечной оси;
– число витков эквивалентной обмотки ротора по продольной и поперечной оси; 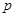 – число пар полюсов.
– число пар полюсов.
Для решения системы уравнений (3) необходимо знать значения параметров СРД, которые можно определить по [3].
Если при преобразовании системы уравнений (3) величины, выраженные в относительных единицах, обозначить теми же символами, что и в физических единицах, то уравнения равновесия напряжений будут иметь вид, аналогичный (3). Однако дифференцирование при этом будет производится по времени, выраженному в электрических радианах. В дальнейшем будут рассматриваться только приведенные параметры СРД, и уравнения равновесия напряжений будут иметь вид (3), в которых потокосцепления определяются следующим образом:
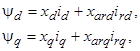
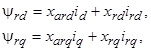 (4)
(4)
где 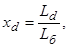
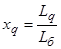 – синхронные индуктивные сопротивления по продольной и поперечной осям;
– синхронные индуктивные сопротивления по продольной и поперечной осям; 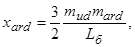
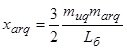 – сопротивления взаимоиндукции между обмотками статора и ротора;
– сопротивления взаимоиндукции между обмотками статора и ротора; 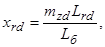
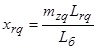 – полные индуктивные сопротивления обмоток ротора;
– полные индуктивные сопротивления обмоток ротора; 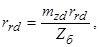
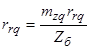 – активные сопротивления обмоток ротора.
– активные сопротивления обмоток ротора.
Для исследования электромеханических переходных процессов необходимо рассматривать наряду с уравнениями равновесия напряжений (3) уравнение движения ротора:
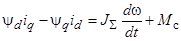 , (5)
, (5)
где 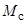 – момент сопротивления на валу;
– момент сопротивления на валу; 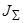 – инерционная постоянная вращающихся масс.
– инерционная постоянная вращающихся масс.
Для исследования синхронного режима СРД при переменной частоте необходимо ввести относительные значения частоты и напряжения:
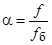 ,
, 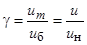 ,
,
где f, u – текущие значения частоты и подводимого напряжения; 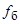 ,
, 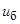 – базисные значения частоты и напряжения.
– базисные значения частоты и напряжения.
Угловую частоту вращения w целесообразно выразить через скольжение: 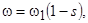 где
где 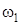 – синхронная угловая частота вращения магнитного поля, созданная обмоткой статора. В относительных единицах
– синхронная угловая частота вращения магнитного поля, созданная обмоткой статора. В относительных единицах 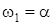 , так как:
, так как:
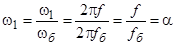 .
.
Связь между углом нагрузки 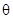 и скольжением
и скольжением 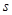 определяется следующим известным выражением:
определяется следующим известным выражением:
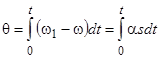 .
.
Откуда скольжение равно: 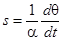 .
.
В результате получаем систему дифференциальных уравнений в относительных единицах:
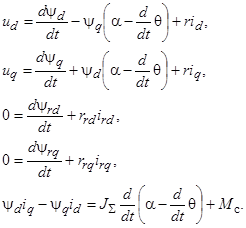 (5)
(5)
Для моделирования переходных процессов в среде MathCAD исходная система уравнений (5) преобразуется в систему итерационных уравнений с добавлением уравнений, позволяющих задавать изменение управляющих (напряжения и частоты питающей сети) и возмущающего (момент нагрузки) воздействий в процессе разгона.
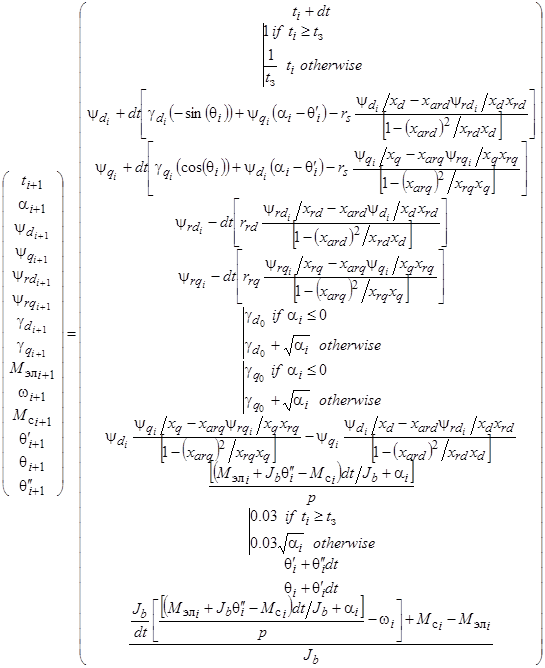
В результате, получена модель, позволяющая исследовать различные законы управления электроприводом, при различном характере нагрузки (при исследовании различных типов жидкостей), для обеспечения синхронного режима работы.
С помощью полученной модели также можно оценить время работы двигателя в асинхронном режиме и в режиме вхождения в синхронизм в начальный момент пуска (рис. 4), при заданном изменении момента нагрузки и выбранном законе управления. Что в свою очередь позволяет рассчитать нижний предел измерения по скорости вращения.
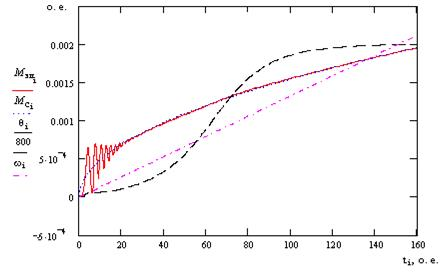
Рис. 4. Переходные процессы: 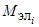 – электромагнитный момент двигателя;
– электромагнитный момент двигателя;
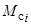 –изменяющийся момент нагрузки;
–изменяющийся момент нагрузки; 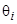 – угол нагрузки;
– угол нагрузки; 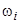 – частота вращения;
– частота вращения;
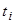 – время. Все величины отсчитываются в относительных единицах
– время. Все величины отсчитываются в относительных единицах
В результате исследования динамики можно сделать следующие выводы: время работы в асинхронном режиме и режиме вхождения в синхронизм будет зависеть от начального значения питающего напряжения, от выбора закона управления и от скорости нарастания частоты.
При увеличении начального значения питающего напряжения, время работы в асинхронном режиме увеличивается, связанно это, прежде всего с увеличением ударного значения переходного электромагнитного момента двигателя и увеличением числа колебаний (декремент затухания изменяется мало, при неизменном характере и величине нагрузки).
Время работы двигателя в режиме втягивания в синхронизм, с увеличением начального значения напряжения, уменьшается, что частично компенсирует влияние увеличения времени работы в асинхронном режиме на общее время работы в несинхронном режиме. Таким образом, регулирование нижнего предела измерения по скорости, с помощью задания начального значения напряжения, зависит от возмущающего воздействия и является в общем случае мало эффективным. Кроме того, максимальное значение начального напряжения, рассчитанное исходя из номинального тока двигателя и активного сопротивления обмотки статора, составляет 35В, и не должно превышать этого значения, то есть возможность регулирования времени вхождения в синхронизм за счет этого параметра сильно ограниченно допустимым режимом работы двигателя. Выбор начального значения напряжения и скорость его нарастания в момент пуска будет зависеть от характера нагрузки.
Наименьшее время вхождения в синхронизм обеспечивает пропорциональный закон управления вида 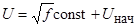 . Здесь следует учитывать, что двигатель, при использовании данного закона движения, работает в самых неблагоприятных условиях, так как в обмотках имеют место наибольшие токи. Скорость вхождения в синхронизм при этом законе управления в реальных единицах составляет 1,58 об/мин (при
. Здесь следует учитывать, что двигатель, при использовании данного закона движения, работает в самых неблагоприятных условиях, так как в обмотках имеют место наибольшие токи. Скорость вхождения в синхронизм при этом законе управления в реальных единицах составляет 1,58 об/мин (при 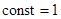 и времени разгона 2 мин.).
и времени разгона 2 мин.).
Наибольшее время вхождения в синхронизм показывает пропорциональный закон управления вида 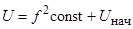 , двигатель при данном законе управления работает в наиболее благоприятных условиях. Скорость вхождения в синхронизм при этом законе управления, при прочих равных условиях, в реальных единицах составляет 1,9 об/мин, что на 17% больше чем при первом из описанных законов.
, двигатель при данном законе управления работает в наиболее благоприятных условиях. Скорость вхождения в синхронизм при этом законе управления, при прочих равных условиях, в реальных единицах составляет 1,9 об/мин, что на 17% больше чем при первом из описанных законов.
При уменьшении скорости нарастания частоты питающей сети время вхождения в синхронизм изменяется незначительно, однако за счет того, что частота вращения двигателя нарастает медленнее, скорость вхождения в синхронизм уменьшается (рис. 5).
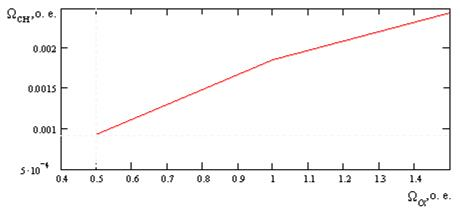
Рис. 5. Зависимость скорости вхождения в синхронизм
от скорости нарастания частоты питающей сети
В свою очередь увеличивается и время проведения одного цикла измерений, которое согласно условиям измерений, составляет 4 мин. Таким образом, эти два условия являются взаимоисключающими. Можно предложить три пути разрешения этой задачи: 1) выбор компромиссных значений: времени проведения цикла измерений и скорости вхождения в синхронизм (нижнего предела измерения по скорости); 2) определение недостающих точек характеристики, на этапе математической обработки результатов путем аппроксимации; 3) комбинация двух первых путей.
Литература
1. Неньютоновские жидкости: Гидромеханика, перемешивание и теплообмен: Пер. с англ. / У. Л. Уилкинсон. – М.: Мир, 1964. – 216 с.
2. Шпаков В.И. Синхронные реактивные двигатели с улучшенными энергетическими и массогабаритными показателями: Диссертация на соискание ученой степени кандидата технических наук: Спец. 05.09.01. / В. И. Шпаков; Томский политехнический институт; Науч. рук. Е. В. Кононенко. – Томск: Б.и., 1988. – 270 л.
3. Кононенко Е.В. Синхронные реактивные машины / Е. В. Кононенко. – М.: Энергия, 1970. – 208 с.

