Для механизмов швейных машин характерны высокие скорости работы, большие ускорения, инерционные усилия движения, звеньев, нестабильные условия процесса и преимущественное применение низких кинематических пар.
Современная швейные машины выполняют до 130–150 переплетений нитей в секунду; кинематические циклы таких машин составляют 7–8 мс, а продолжительность многих этапов процесса менее 1 мс. Скорости мс движения рабочих органов и нитей измеряются десятками м/с, ускорения нити -600 м/с2. При этом частота вращения ведущих звеньев машин составляет 6000–8000 об/мин. Многие параметры c строчки и процессе работы — длина стежков, натяжение нитей, толщина и физико- механические свойства, сшиваемых деталей и нитей-изменяют по технологическим соображением; в машинах с отклоняющимся иглами, кроме того регулируется величина отклонения игл. Вследствие чего изменяются условий взаимодействия рабочих органов механизмов машин.
При проектирование и расчете механизмов переплетения нитей- также другие технологические требования-заданные структуру переплетений нитей, вид строчки, натяжение нитей, особенности их перемещения и многие динамические и конструктивные условия. Механизмы игл производит прокаливания сшиваемых материалов c одновременным проведением них нитей, образования петель-напусков и отклонение игл. В большинстве механизмов игл для прокаливания сшиваемых деталей образовано звеньев c низкими кинематическими парами, которые при высоких скоростях звеньев, возникают колебания отдельных звеньях целом в машины.
При выборы структуры игольного механизма целесообразно проанализировать влияние дезаксиала и расположения шатуна на движение иглы, а также установит рациональное число опор игл водителя, связанное созданием различных частоты колебания отдельных звеньев. Перемешенное игл водителя в зависимости от игла поворота кривошипа отсчитываемого от верного вертикального положения определятся по формуле:
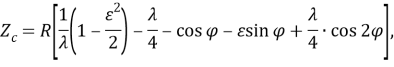
где 
; 
, 
радиус кривошипа, длины шатуна и дезаксиал. Графики функции 
(+) позволяет, судит о влиянии структуры механизма на продолжительность рабочего хода иглы. Параметры с
и 
позволяет исследовать малых колебаний звеньев игольного механизма в процессе работ.
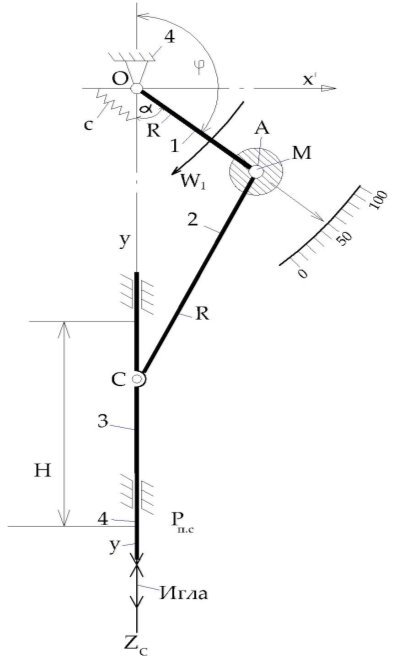
Рис. 1. Схема экспериментальной установки для определения малые колебания игольного механизма швейных машин: 1- кривошип, 2- шатун, 3- игловодитель, 4- стойка.
Одним из пути повышение надежности швейных машин является снижение колебания в шарнирах механизма иглы, работающих на высоких скоростях. На рис.1 показана универсальный широко применяемые тип игольного механизма швейных машин швейного и обувного производства легкой промышленности.
Кривошип 1 вращаясь, приводит во влияние шатуна 2, совершает возвратно поступательное движение вместе иглой 4.
В точки А кривошипа установлен прибор с измерительным устройством, во вращательном движение стрелки 1. Каждому положению игл водителя соответствуют определенное значение измеряемой величины, которое указываются стрелкой на шкале прибора (1). Это соответствие нарушается, если стойка кривошипа вибрирует. Тогда стрелка 1, совершает малые колебания относительно среднего положения, которые может не совпадать с положением, соответствующим статическому равновесию.
Обозначим через 
значение угла 
, определяющее положение стрелки 1, при отсутствии вибрации стойки и через 
среднее значение угла при колебания кривошипа.
Разность 
даёт динамическую ошибку в показаниях прибора. Такая же ошибка получается в случае, если к игл водителю механизма, звенья которого находились в положении статического равновесия, приложит периодически изменявшеюся силу 
т. е. усилие прокола материала.
Положение устойчивого статического равновесия звеньев игольного механизма соответствует минимум потенциальной энергии механизма иглы 
учитываем только массу 
, сосредоточенную в точке А и упругость пружины c, помешенной между стойкой и кривошипа 1:
(1.1)
Где: 
обобщённая координата игольного механизма;
постоянная величина потенциальной энергии,
определяемое началом отсчета;
коэффициент угловой (крутильной) жесткости пружины;
длины звеньев кривошипа и шатуна.
При двукратном дифференцировании выражения потенциальной энергии механизма по обобщённой координате получаем:
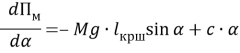(1.2.)
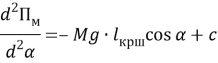(1.3.)
При условий 
положение устойчивого равновесия характеризуется корнем уравнения.
(1.4.)
При определением кинематической энергии механизма иглы 
учитываем только энергию сосредоточенной массы :
(1.5.)
Исследуем сначала свободные колебания механизма иглы около положением статического равновесия, принимая её обобщённую координату отклонение
(1.6.)
Тогда выражение потенциальной энергии механизма (1.1.) принимает вид:
(1.7.)
Из разложения в ряд Маклерона в окрестности значения 
получаем приближеннее выражение потенциальной энергии механизма.
(1.8.)
Где штрихи обозначают дифференцирование по 
в дальней полагаем 
, что соответствует изменению начало отсчёта потенциальной энергии механизма. Величина 
также равна нулю по условию (1.4.). Следовательно,
(1.9.)
т. е. квази упругой (обобщённой) коэффициент жесткости 
имеет вид:
(1.10)
Уравнение движение игольного механизма при свободных колебаниях имеет вид:
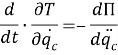или
(1.11)
Следовательно, собственная частота игольного механизма
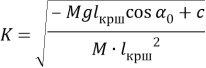(1.12)
Зависит от положение статического равновесия. При исследовании вынужденных колебаний представим обобщённую координату в виде суммы:
(1.13)
Где: 
дополнительное перемещение,вызываемое периодически изменяющейся силой .Подставляя значение из соотношения (1.6.), получаем:
(1.14)
При малых колебаниях можно заменит переменную величину 
её средним значением
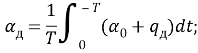(1.15)
Где: 
период колебаний.
Тогда 
, и вынужденные колебания можно рассматривать как колебания относительно положения динамического равновесия, определяемого углом 
. Уравнение движения игольного механизма в этом случае имеет вид:
(1.16)
где: 
приведённый к звену 1 момент от силы .
При равенстве длин кривошипа и шатуна перемещение игл водителясвязано с углом поворота
соотношением
(1.17)
где: 
ход иглы, мм.
Отсюда передаточное отношение
приведённый момент 
находим из условия
или
(1.18)
разложение в степенной ряд в окрестности 
даёт приближенное значение приведённого момента
(1.19)
приближенное значение потенциальной энергии механизма теперь находим из разложения в ряд в окрестности
или что тоже
:
отсюда
(1.20)
подставляя выражения для 
и 
в уравнение (1.16) получаем уравнение малых колебаний игольного механизма при действии вынуждающий силы полезного сопротивления 
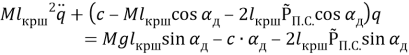(1.21)
полученное линейное уравнение с периодическим коэффициентом приводится к неоднородному уравнение Хилла. Если сила изменяется по гармоническому закону:
то уравнение (1.21) приводится к неоднородному уравнению
Матье
(1.22)
где:
постаянные величины.
Тогда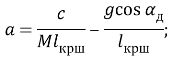
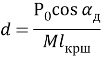
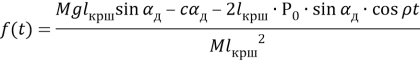(1.23)
По уравнение (1.23) можно исследовать устойчивости движения, используя свойства коэффициентов уравнения Матье.
При этой исследовании достаточно предположит, что положения динамического равновесия, т. е. значение угла находится в пределах рабочего диапазона. Для определения самой величины , характеризующей динамическую ошибку игольного механизма можно использовать приближенный метод, основанный на близости величин 
и .
К рассмотрению уравнения (1.23) приводится также задача о влиянии возвратно поступательной вибрации стойки по гармоническому закону в направлением движения игл водителя, игольного механизма швейной машины.
Литература:
- Н. И. Левитский Теория механизмов и машин. М, «Наука» 1979, 576с
- Н. М. Вальщиков и др. Расчёт и проектирование машин швейного производства. Л, «Машиностроение» 1973, 344с.
- А. И. Комиссаров и др. Проектирование и расчёт машин обувных и швейных производств. М, «Машиностроение» 1978, 427с.
- И. Г. Русаков и др. Вынужденные колебания систем, ударяющихся об ограничитель. Журнал технической физики. Вып.11–12 1982.
