Работа посвящена численному моделированию задач изгиба и колебаний вязкоупругих пластин сложной формы при различных моделях вязкости.

Ключевые слова: жесткость вязкоупругих пластин, изгиб, коэффициент Пуассона, объемный модуль упругости, R — функция,полные системы координатных функций.

Математическая модель задач изгиба вязкоупругих пластин описывается уравнением

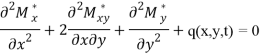(1)

Если при формулировке основных физических соотношений используется гипотеза о постоянстве коэффициента Пуассона, изгибающие и крутящие моменты определяются следующими зависимостями:

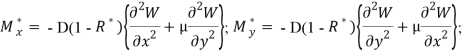
(2)

где D- жесткость вязкоупругих пластин; интегральный оператор с ядрами релаксации R(t), т. е. 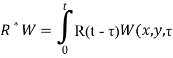)d — прогиб пластины;

µ — коэффициент Пуассона; q (x, y, t)-интенсивность внешней нагрузки.

Если же используется гипотеза об упругости объемных деформации, тогда для изгибающих и крутящего моментов справедливы зависимости

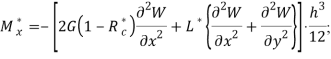
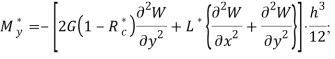(3)

где G=E/2(1+µ) — модуль сдвига; E — модуль упругости; — интегральный оператор с ядрами сдвиговой релаксации — интегральный оператор, т. е.

K=E/3(1- 2µ) — объемный модуль упругости; h — толщина пластины.

Для получения уравнения движения достаточно вместо q(x,y,t) в уравнение (1) подставить выражение q(x,y,t) — ρh и получим следующие уравнение колеблющейся тонкой вязкоупругой плиты

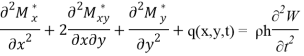(4)

где ρh — масса плиты, отнесенная к единице поверхности.

Уравнения (1) и (4) решаются при соответствующих граничных и начальных условиях

(5)

где — дифференциальные операторы, зависящие от граничных условий; Г — граница области; и начальные значения.

Решения уравнений (1) и (4) ищем в виде

W(x,y,t)=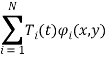(6)

где - полные системы координатных функций (полиномы Чебышева, степенные, тригонометрические, сплайны Шенберга и т. д.) СКФ, удовлетворяющие всем граничным условиям, которые строятся с помощью метода R — функций В. Л. Рвачева [1]; — неизвестные функции, являющиеся функциями времени t.

После применения метода Бубнова — Галеркина решение уравнения (1) и (4) сводится к решению системы интегральных (ИУ) и интегро-дифференциальных уравнений (ИДУ) относительно функций времени. Отметим, что при решении задач изгиба и колебаний вязкоупругих пластин сложной формы используется ортонормированные СКФ по бигармоническому и единичному операторам соответственно. Здесь использование ортонормированной СКФ существенно облегчает решение систем интегральных и ИДУ.

В случае задачи изгиба после ортонормированные СКФ по бигармоническому оператору основные разрешающие уравнений приводятся к автономным системам ИУ. В случае задачи колебаний, основные разрешающие уравнений с помощью метода разложения собственных форм колебаний, приводятся к автономным системам ИДУ. Для решения автономным систем интегральных и ИДУ применяется численный метод, основанный на использовании квадратурных формул [2]. На основе этого метода описан алгоритм численного решений.

Исследована сходимость вычислительного алгоритма и показана достоверность результатов, полученных с помощью комплекса программных средств путем их сопоставления с точным решением или решениями, полученными другими авторами.

Рассмотрим задачи изгиба вязкоупругой пластины (рис.1). Пусть пластина, материал, который характеризуется упругими объемными деформациями, жестко защемлена по всему контуру и находится под действием равномерно распределенной нагрузки (q=1). Исследуется характер поведения прогиба W, изгибающих , и крутящего моментов в зависимости от изменение границы области. В качестве ядра сдвиговой релаксации используется ядро R(t)=ε.

Уравнение геометрии области для пластины, представленной на рис.1, имеет вид:

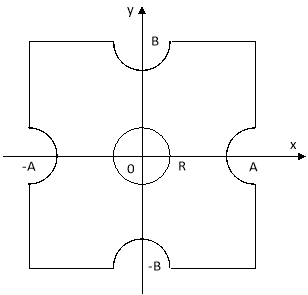
Рис. 1.

Ω=(((Ω ₁ (Ω ₃ Ω ₅)))(Ω ₂ (Ω ₄ Ω ₆))) Ω ₇

где Ω ₁ =(a²-x²)/2a, Ω ₂ =(b²-y²)/2b,

Ω ₃ =((x+a)²+y²-R²)/2R, Ω ₄ =(x²+(y+b)²-R²)/2R

Ω ₅ =((x-a)²+y²-R²)/2R, Ω ₆ =(x²+(y-b)²-R²)/2R, Ω ₇ =(x²+y²-R²)/2R

_— оператор логический конъюнкции нулевого порядка.

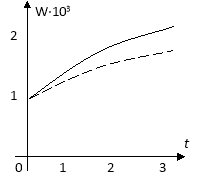
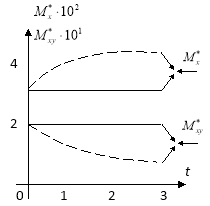
На рис.2, а показано изменение прогиба во времени (пунктирная линия) в точке с координатами х=0.5; у=0.5, а на рис.2,б — изменение изгибающего и крутящего моментов (пунктирная линия) в той же точке.

а) б)

Рис. 2. а, б

Для сравнения на тех же рисунках (сплошными линиями) показано изменение тех же величин для пластины с постоянными во времени коэффициентом Пуассона и ядром релаксации, совпадающим с ядром R_c(t) для рассматриваемой пластины.

Результаты получены при следующих значениях безразмерных параметров:

Λ=a/b=1; r=R/a=0.2; ε=0.05; β=0.075; µ=0.17

Из рис.2 видно, что если материал вязкоупругих пластин характеризуется упругими объемными деформациями, тогда даже при постоянных внешних нагрузках прогиб, изгибающий и крутящий моменты изменяется, т. е. прогиб и изгибающий момент увеличивается во времени, а крутящий момент уменьшается. Результаты полученные на основе гипотезы об упругости объемных деформаций хорошо согласуются с результатами эксперимента. Однако для простоты в инженерных расчетах часто делается предположение, что коэффициент Пуассона является постоянной во времени величиной. А также результаты получено для пластины с постоянным во времени коэффициентом Пуассона при использовании различных ядер релаксации, в частности, ядер экспоненциального вида, ядер Ржаницына — Колтунова и Абеля. Результаты показывает, когда в качестве ядра релаксации используется ядра Абеля, то с увеличением времени t значение прогиба увеличивается гораздо быстрее. Поставленная задача решена при различных значениях безразмерных параметров. Сравнительный анализ показывает, что частично изменение формы границы области приводит к довольно существенному изменению напряженно-деформированного состояния пластин.

Далее рассмотрим вынужденные колебания жестко защемленных вязкоупругих пластин (рис.1) и находящихся под действием равномерно распределенной нагрузки при начальных условиях W|_t=0=0, W^t|_t=0=0. В качестве ядра сдвиговой релаксации используется экспоненциальное ядро.

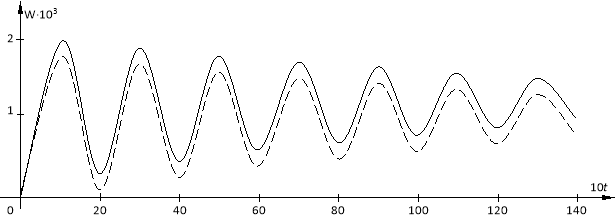
Рис. 3.

Результаты получены при следующих значениях безразмерных параметров:

Λ=a/b=1; r=R/a=0.2; ε=0.05; β=0.075; µ=0.17

На рис.3 показано изменение прогиба пластины W(0.5;0;t) во времени t (пунктирными линиями), полученные на основе гипотезы об упругости объемных деформаций. Для сравнения сплошными линиями показано изменение прогиба пластины W(0.5;0;t), полученное на основе гипотезы о постоянстве коэффициента Пуассона. Из рисунка видно, что учет упругости объемных деформации приводит к уменьшению амплитуды колебаний, а процесс затухания происходит медленно. Отметим, что при ε=0 процесс колебаний вязкоупругих пластин совпадает с процессом колебаний упругих пластин. Интересно отметить, что при ε<0.001 мы фактически рассматриваем процесс колебаний упругой пластины, и надо подчеркнуть, что при ε=0,1 процесс затухания колебаний происходит быстрее, чем ε=0,05 и ε=0,001.

Задача решена при различных значениях безразмерных параметров, подробно исследовано влияние учета вязкоупругих свойств материала на амплитуду и частоту колебаний в зависимости от внешней нагрузки и граничных условий. Учет вязкоупругих свойств материала пластинки приводит к снижению амплитуды колебаний и вызывает ее затухание по экспоненциальному закону. При затухании колебаний огромную роль играет реологический параметр ε.

Численные результаты показывает, что выбор той или иной гипотезы при формулировке физических соотношений приводит к довольно существенному изменению напряженно-деформированного состояния пластин.

На основе предложенного алгоритма задач разработан комплекс программных средств, с помощью которых оперативно решаются задачи наследственной теории вязкоупругости для тел с произвольной конфигурацией [3–4].

Литература:

1. Рвачев В. Л., Курпа Л. В. R-функций в задачах теории пластин. Киев: Наукова думка.1987.176 с.
2. Бадалов Ф. Б. Методы решения интегральных и интегро-дифференциальных уравнений наследственной теории вязкоупругости. Ташкент. Мехнат.1987.289 с.
3. Назиров Ш. А., Садиков Х. С. Комплекс программных средств для решения краевых задач вариационными методами./Алгоритмы. Ташкент: РИСО АН Уз.Вып.65.1988.
4. Садиков Х. С., Халилов А. Ж. Компьютерное моделирование и исследование краевых задач вязкоупругости произвольной конфигурации в среде системе Maple. Материалы научно-технической конференции «Перспективы науки и производства химической технологии в Узбекистане». Навои. 22–24 мая 2014 г. С. 247–248.