В связи с тем, что федеральный государственный образовательный стандарт устанавливает новые требования к метапредметным результатам освоения основной образовательной программы, возникает необходимость в разработке специальной системы заданий, направленной на формирование и дальнейшее развитие метапредметных умений школьников в процессе обучения математике.
Одной из основных содержательных линий школьного курса алгебры является линия тождественных преобразований (учение о числе, функции, уравнения и неравенства, тождественные преобразования).
Стоит отметить большое практическое значение тождественных преобразований иррациональных выражений в школьном курсе математики. Изучение тождественных преобразований служит аналитическим аппаратом при:
– доказательстве теорем и выводе формул;
– решении уравнений, неравенств и их систем;
– упрощении выражений;
– нахождении значений выражений;
– исследовании функций и др.
Тождественные преобразования (особенно в комплексе с решением уравнений, неравенств, систем) находят широкое применение в смежных дисциплинах (физика, химия) при работе с формулами, решении содержательных задач, подготавливают обучающихся к восприятию таких важнейших понятий, как алгоритм, программа и др.
Разрабатывая систему заданий метапредметного характера по данной теме, для наилучшего закрепления умений и навыков, приобретаемых при изучении тождественных преобразований в первую очередь необходимо расширить и углубить пользование алгебраической терминологией и символикой. Для этого необходимо включать в процесс обучения тождественным преобразованиям иррациональных выражений задачи следующего содержания: «Прочитать выражение»:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() .
.
Такие задания развивают связную математическую речь обучающихся, что в свою очередь обеспечивает сознательность учения, ускоряет развитие мышления как совокупности логических операций, способности рациональному оперированию знаковыми системами, пространственным представлениям, а также запоминанию и воображению.
Изучение тождественных преобразований предоставляет большие возможности для формирования таких качеств математического мышления, как гибкость, критичность и самостоятельность. Для безошибочного выполнения обучающимися тождественных преобразований иррациональных выражений необходимо формировать у них навыки самостоятельного контроля.
Одним из метапредметных умений, служащих инструментом при формировании навыков самоконтроля является умение называть сделанные ошибки. Приведём пример такого задания:
На каком шаге допущена ошибка?
![]() .
.
Приведём ещё один пример задания на формирование самоконтроля в процессе изучения тождественных преобразований иррациональных выражений: найдите ошибку в формулировке задания: «Между какими из следующих пар выражений: ![]() и
и ![]() ,
, ![]() и
и ![]() можно поставить знак равенства».
можно поставить знак равенства».
В систему упражнений целесообразно включить задания, которые формируют умение строить цепочки логических рассуждений.
Приведём пример такого задания:
Какие из следующих выражений являются тождественно равными?
a) 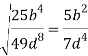 ;
;
b) 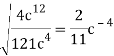 ;
;
c) 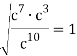 .
.
Начиная изучение тождественных преобразований иррациональных выражений следует просить обучающихся объяснять каждый шаг преобразования, сформулировать те правила и законы, которые применяются. Такой вид деятельности на уроке позволяет сформировать у обучающихся навык составления плана выполнения учебной задачи с помощью учителя и самостоятельно.
Например:
Составьте план выполнения следующего задания:
Докажите тождество: ![]() .
.
Сформировать умения обучающихся по выявлению условий можно с помощью следующего упражнения:
Какие из следующих выражений могут быть преобразованы вынесением общего множителя за скобки?
a) ![]()
b) ![]() ;
;
c) ![]() .
.
Одними из важных метапредметных умений являются умения определять понятия, создавать обобщения, устанавливать классификации и самостоятельно выбирать основания и критерии для классификации.
Пример задания на установление классификаций:
Разбейте выражения на группы:
![]() .
.
Укажите, по какому признаку вы разбивали данные выражения.
Сформировать умение осознанно использовать речевые средства в соответствии с задачей позволяет следующее задание:
Предложите формулировку задания к данному выражению:
1) ![]() ;
;
2) ![]()
Приведём пример заданий, направленных на формирование умений самостоятельно определять цели учебной деятельности:
1)Уточните цель выполнения следующего задания:
Избавьтесь от иррациональности в знаменателе: ![]() .
.
2)Чему вы научитесь, выполнив следующее задание:
Докажите тождество: ![]() .
.
Включение заданий, предложенных выше, в процесс обучения математике, в частности обучения тождественным преобразованиям иррациональных выражений, позволяет формировать метапредметные умения школьников. Стоит отметить, что данные задания могут быть предложены обучающимся при изучении любой другой темы школьного курса математики, Регулярное выполнение метапредметных заданий позволяет совершенствовать навыки и умения учеников.
Литература:
- Федеральный государственный образовательный стандарт среднего (полного) общего образования (утвержден приказом Минобрнауки России от 17 мая 2012 г. № 413).
- Тумашева О. В., Берсенева О. В. Обучение математике с позиции системно-деятельностного подхода: монография; Краснояр. гос. пед. ун-т им. В. П. Астафьева. — Красноярск, 2016. — 280 с.
- Асмолов А. Г. Системно-деятельностный подход в разработке стандартов нового поколения // Педагогика. 2009. № 4. С. 18–22.

