Модель гравитационного поля планеты в системе гравитирующих стержней



Моделирование внешнего гравитационного поля Земли важно для вычисления траекторий естественных и искусственных тел. Простейшую модель центрального поля шара построил Ньютон. Учет несферичности Земли привел к использованию разложения потенциала по сферическим функциям. Значения параметров разложения приближенно определяются по наблюдениям Луны, ИСЗ и по гравиметрическим и геодезическим измерениям. Известный набор значений получил название «Стандартная Земля». Перечисленные сведения можно найти в книге Аксенова Е. П. [1]. Хорошее приближение дает модель двух неподвижных центров [1]. Обобщением является построение системы из многих материальных точек [5]. В нашей задаче используется модель из нескольких гравитирующих стержней, жестко связанных с Землей [4], а также модели, состоящие из «зубцов» и из «кочек». Введем геоцентрическую цилиндрическую систему координат R, θ, z. Ось z направим вдоль оси вращения Земли. Перейдем к безразмерным величинам. Для этого введем новую систему единиц. Пусть одна единица длины — 6371 км, единица массы — 5,9726·10²⁴ кг, гравитационная постоянная G = 1. На этой оси поместим набор симметричных относительно начала СК однородных бесконечно тонких стержней, умещающихся на отрезке [-1,1]. Плотность каждого стержня равна . Полагаем, что концы отрезка находятся внутри Земли.

Постановка задачи

Будем строить варианты моделей с одинаковой безразмерной массой, равной единице, которые помещаются в сферу единичного радиуса. Вариант модели обозначим M (S, D, N). Параметр Sописывает структуру — дискретная модель из материальных точек, из кусочно-непрерывных стержней, из точек и стержней соответственно. При этом гладкость линейной плотности стержней может быть различной — на концах стержней может испытывать скачок сама плотность и/либо ее производная, а могут быть непрерывны и плотность и производная (случаи пенька , зубца, кочки). D = 1, 2, 3 означает размерность модели, то есть количество осей, на которых расположены точки и стержни. N — это число элементов модели. Массы, размеры элементов также могут различаться. Простейшим случаем является модель M (point, 1, 1), состоящая из одной материальной точки.

Введем декартову систему координат с началом в центре масс системы. Размазав модель равномерно по оси, получим варианты M (segment(s), 1, 1) с пеньком либо с зубцом, либо с кочкой. Далее, добавляя распределения масс вдоль осей получим варианты M (point, 2, N), M (point, 3, N), M (segment(s), 2, N), M (segment(s), 3, N). Аналогично можно поступить с вариантами M (point & segment(s), D, N), располагая вперемежку точки и стержни. Ограничимся моделями с зеркальной симметрией относительно плоскости , но при этом будем строить модели с ротационной симметрией. В этом случае можно рассматривать вращение системы.

Введем новую характеристику гравитационного поля системы — квазикруговую скорость (ККС) с помощью скалярного произведения:

В системе с ротационной симметрией относительно оси и зеркальной симметрией она совпадает с обычной круговой скоростью при:

Нужно построить для рассматриваемого потенциала изолинии ККС в трех координатных плоскостях — экваториальной двух меридиональных — и . В случае сферической модели все изолинии будут окружностями.

Типы рассматриваемых распределений масс:

1. Разрывное кусочно-постоянное распределение
2. Непрерывное кусочно–линейное пилообразное распределение

Построим кусочно-линейное распределение масс, график которого имеет пилообразный вид. Расположим нечетное количество зубцов n симметрично относительно начала СК на оси z. Зубцы образуют равнобедренные треугольники с основаниями 2и высотой , где k — номер зубца. Зубцу приписываем массу [4]. Считаем, что зубцы не пересекаются друг с другом, а крайние зубцы не выходят за интервал [-1,1].

3. Гладкое кусочно-параболическое распределение

Построим гладкое кусочно-параболическое распределение, график которого имеет вид «кочек». Функция плотности одного элемента состоит из 3 частей, каждая из которых является частью параболы. Масса «кочки» равна , основание 2, середину основания обозначим .

При получаем дельта-функцию, которая отображает точечную массу величиной . Положение материальной точки совпадает с координатой .

Гравитационное поле

Введем новую характеристику гравитационного поля системы — квазикруговую скорость (ККС). Рассмотрим изолинии ККС для каждого вида потенциала. ККСвводим с помощью скалярного произведения:

(1)

Это выражение является вириалом. Вириал для системы точек массами имеет вид [6]:

.(2)

Так как — потенциал модели, то уравнения движения будут иметь вид:

(3)

Выразив из (3) и подставив в выражение (2), получим выражение (1). Теорема вириала гласит, что усредненная по бесконечному интервалу времени кинетическая энергия механической системы равна усредненному по тому же интервалу вириалу сил. Следовательно, введенная ККС является характеристикой гравитационного поля.

Рассмотрим изолинии ККС для различных моделей. Сначала исследуем модель двух стержней постоянной плотности на оси (Рис.1).

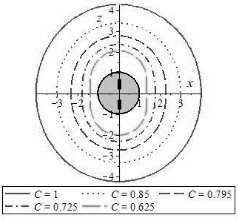
Рис. 1. Изолинии ККС в меридиональной плоскости

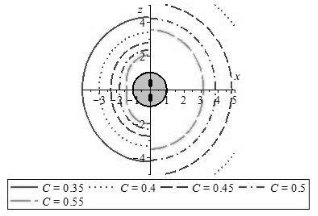
Рис. 2. Изолинии ККС. Слева , справа

В экваториальной плоскости изолинии будут окружностями, так как влияние стержней одинаковое в любой момент времени, потому что располагаются они на оси . Из-за ротационной симметричности модели график изолинии в любой меридиональной плоскости будет одинаковым. Изолинии ККС вытягиваются вдоль оси , округляясь по мере отдаления от центра. При изменении типа распределения стержня на зубчатый, изолинии отдаляются от центра (Рис. 2).

Исследуем, как изменение гладкости распределения отразится на виде изолиний. На рис. 3 сравнены две модели — с зубчатым и кочкообразным распределением. Как видно из рисунка, увеличение порядка гладкости отражается незаметно, вид изолиний идентичен.

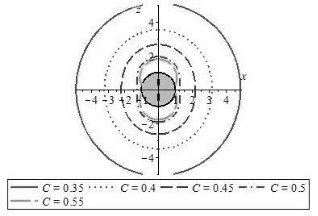
Рис. 3. Изолинии ККС Слева , справа

Заключение

Предлагаемая модель внешнего гравитационного поля Земли является довольно гибкой благодаря наличию большого числа параметров. Изменяя вид распределения можно достичь хорошего приближения к выражению внешнего потенциала Земли как суммы кеплерова потенциала и возмущающей части.

Модели такого рода можно строить и для других планет Солнечной системы. Значения параметров могут приближенно определяться по известным данным о некоторых планетах.

Литература:

1. Аксенов Е. П. Теория движения искусственных спутников Земли. М.: Наука, 1977. 360 с.
2. Кутузов С. А. Математическое описание астрономических систем. Учеб. пособие.-СПб.: Изд. СПбГУ, 2004. 244 с.
3. Антонов В. А., Никифоров И. И., Холшевников К. В. Элементы теории гравитационного потенциала и некоторые случаи его явного выражения. СПб.: Изд-во С.-Петерб. ун-та, 2008. 208 с.
4. Кодрик В. В., Кутузов С. А. Моделирование внешнего поля Земли с помощью гравитирующих стержней //Труды XLII международной научной конференции аспирантов и студентов «Процессы управления и устойчивость» / Под ред. А. С. Еремина, Н. В. Смирнова.-СПб, издат. дом СПбГУ, 2011. 588с. с. 145–150.
5. Антонов В. А., Тимошкова Е. И., Холшевников К. В. Введение в теорию ньютоновского потенциала. М.: Наука, 1988. 272 с.
6. Огородников К. Ф. Динамика звездных систем, М: Физматгиз, 1958. 644 с.