Моделирование влияния поверхностных состояний на электронные свойства квантовой точки InSb



Численное моделирование электронных процессов в квантовых точках (КТ) представляет особый интерес, поскольку экспериментально многие важные свойства таких объектов бывает трудно изучить ввиду их нестабильности, одной из причин которой могут являться поверхностные состояния на границах КТ [1,2,3].

Частицы антимонида индия (InSb), получаемые методом механического измельчения и последующим химическим травлением [4], теоретически можно относить к КТ. Это обусловлено тем, что за счет наименьшей эффективной массы носителей заряда по сравнению с другими полупроводниковыми материалами, квантоворазмерные эффекты в InSb могут наблюдаться в относительно больших объектах (порядка 100 нм) [5]. Обратной стороной указанного метода получения выступают явления, связанные с дефектами в объеме и на поверхности материала [6]. Такие состояния могут возникать по разным причинам, например, в результате механических нарушений структуры после процедуры измельчения или из-за остатков травителя на поверхности кристалла.

Целью работы было исследовать влияние поверхностных состояний (ПС), обусловленных обрывом кристаллической решётки, на электронные свойства сферической КТ InSb, в частности, построить ее физическую модель с ПС и получить распределение носителей заряда в центральном сечении КТ.

Математическая модель квантовой точки с ПС

Для определения влияния ПС на электронные свойства InSb, необходимо решить уравнение Шредингера с учётом распределения электрического потенциала в объёме и на поверхности образца. В качестве модели рассмотрена сферическая КТ InSb диаметром 40 нм (рис. 1). Для определения распределения потенциала требовалось решить уравнение Пуассона для выбранной модели. Для простоты расчетов считалось, что все ПС являются акцепторными и температура такова, что все ПС ионизованы, т. е. все оборванные связи скомпенсированы электронами из приповерхностной области. В связи с тем, что обрыв периодичности решетки в основном происходит на крайнем атоме материала, для построения модели ПС удобно выделить в КТ участок толщиной в 1 атом. Размеры атомов сурьмы и индия с точки зрения потенциала определяются величиной постоянной решетки а — 0,648 нм. Вместе с ПС необходимо выделить приповерхностные области (ПО), чтобы определить, как изменится ход потенциала в КТ с учётом ПС. ПО (2 и 3) аналогично ПС (1) представляют собой атомарный слой толщиной 0,648 нм и отличаются друг от друга энергией взаимодействия носителей заряда с вакансиями, образующимися на поверхности КТ. Важно выделять области 2 и 3 при моделировании, поскольку решение уравнения Пуассона в них будет отличаться из-за разных плотностей заряда, обусловленных обеднением этих областей электронами.

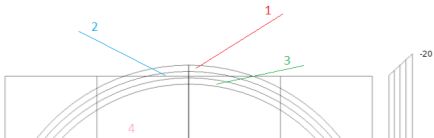
Рис. 1. Схематическое изображение модели КТ с ПС толщиной в 1 атом: 1) ПС на границе образца; 2,3) приповерхностные области для определения изменения хода потенциала в КТ; 4) объем КТ

Для перехода носителей заряда из приповерхностной области, необходимо, чтобы они обладали энергией большей или равной энергии ионизации атомов в составе InSb. Так как все акцепторы ионизованы, можно рассчитать силу взаимодействия между вакансиями на поверхности КТ и электронами ПО 2 и 3:

(1)

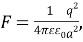
В данном рассмотрении не учитывается взаимодействие между образовавшимися вакансиями в области 2 и электронами из области 3, поскольку это сильно усложнило бы расчёты.

Умножив силу взаимодействия F на расстояние между электронами, образующими ковалентную связь (соответствует постоянной решетки), получим энергию взаимодействия между вакансиями на поверхности КТ и электронами из областей 2 и 3

(2)

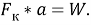
Если энергия взаимодействия W больше или равна энергии ионизации атомов велика вероятность перехода носителя заряда между ними. Для этого необходимо выполнение соотношения:

(3)

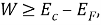
где E _{c —} энергия дна зоны проводимости, E _F — энергия уровня Ферми.

Для определения энергии ионизации использовано соотношение для нахождения энергии уровня Ферми в собственном полупроводнике InSb, энергия рассчитывается от потолка валентной зоны (E _v =0):

(4а)

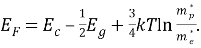
Отсюда:

(4б)

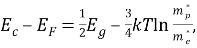
где k — постоянная Больцмана, T — температура, E _g — ширина запрещенной зоны InSb, эффективная масса дырок эффективная масса электронов масса свободного электрона.

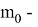
Анализ значения W _1–2 и W _1–3 (см. таблицу 1) показывает, что взаимодействие между поверхностными вакансиями и электронами из ПО 3 на порядок слабее, чем между поверхностными вакансиями и электронами взаимодействия атомов из ПО 2. Величина W _1–3 не удовлетворяет соотношению (3), и из формулы (1) видно, что с увеличением расстояния от границы материала, вероятность перехода носителей заряда между атомами этих областей падает по квадратичному закону. Так как вероятность перехода носителя заряда из объема материала на вакансию атома поверхности относительно мала, в рамках данной модели, такими переходами можно пренебречь.

Прежде чем решать уравнение Шредингера, необходимо знать ход потенциала в сферической КТ. Для достижения более высокой точности результатов расчёта, модель КТ представлена в виде центрального сечения сферы. Центральные сечения сферы представлены в виде доменов 1–4, как это показано на рисунке 2. Нахождение хода потенциала U производится по двумерному уравнению Пуассона:

(5)

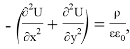
где U –ход потенциала, ρ — поверхностная плотность заряда.

Для определения ρ в ПО использовано следующее равенство:

(6)

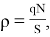
где N — количество атомов в приповерхностной области, S –площадь приповерхностной области.

На поверхности и в объеме материала (области 1 и 4) значения ρ/εε ₀ равны нулю, поскольку в них нет не скомпенсированной плотности заряда. Тогда уравнение Пуассона для этих областей принимает вид уравнения Лапласа:

(7)

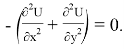
Для расчётов ρ для ПО 2 и 3 необходимо указать радиусы сечений, которые образуют области 1- 4. Радиус сечения для области 1 соответствует радиусу самой КТ. Радиусы доменов 2–4 последовательно уменьшаются на 0,65 нм. Таким образом, выделяются: атомарный слой поверхностных состояний , обусловленных обрывом кристаллической решётки, приповерхностные области

и с разными энергиями взаимодействия носителей заряда с вакансиями на поверхности КТ и электро нейтральный объём КТ .

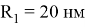
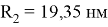
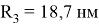
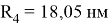
Расчёт числа атомов в i -ой ПО произведён по формуле:

(8)

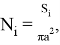
где i = 1, 2, 3.

В правой части уравнения (8) знаменатель — это площадь центрального сечения одного атома, если считать, что атом представляет собой сферу с радиусом равным постоянной решетки. Числитель — это площадь приповерхностной области в сечении КТ.

Площадь приповерхностной области найдена из соотношения:

(9)

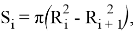
Ранее было принято, что в состоянии термодинамического равновесия, все вакансии, образованные обрывом кристаллической решетки, ионизованы. Поскольку число таких вакансий равно числу атомов и в связи с тем, что в модели рассматриваются переходы электронов из приповерхностных областей 2 и 3 в область 1, можно вычислить поверхностную плотность заряда в этих областях. В приповерхностной области 1 и в объёме КТ .

Из анализа и и в приближении, что от одного атома в область 1 может перейти только один электрон, следует, что более вероятно состояние, при котором все электроны 2-ой ПО перешли в область 1 и оставшаяся часть вакансий в области 1 скомпенсирована электронами из 3-ей области.

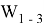
Результаты расчета в Comsol Multiphysics

Для моделирования и расчётов уравнений Пуассона и Шрёдингера в КТ была использована библиотека PDE программного пакета «Comsol Multiphysics». Результаты решения уравнения Пуассона в центральном сечении сферической КТ приведены на рис. 2.

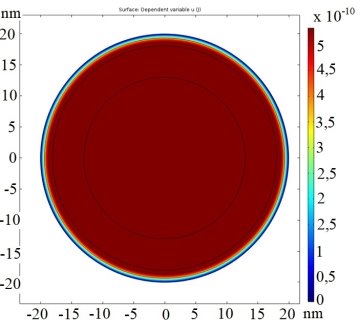
Рис. 2. Распределение потенциала в центральном сечении сферической КТ

Сферическая форма КТ позволяет определить ход потенциала в определённом направлении. Одномерное представление изменения потенциала внутри КТ представлено на рис. 3.

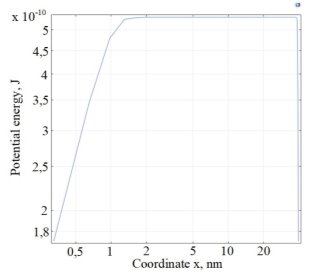
Рис. 3. Распределение потенциала в центральном сечении сферической КТ

Анализ результатов показывает, что значения потенциала, соответствуют аналитическому решению уравнения Пуассона при заданных величинах. Для определения потенциала для последующей подстановки в уравнение Шредингера использовался оператор «General Extrusion», позволяющий выделить в объеме точку с определёнными координатами, и, рассчитать в ней значение потенциала. Как видно из рисунка 2, основные изменения потенциала происходят на границе 1-ой и 2-ой ПО. Поэтому было взято по четыре значения из областей 1 и 2 с последующим расчётом в них среднего значения потенциала. Для областей 3 и 4 взяты значения, соответствующие центральным положениям, то есть, в точке с координатами (0;18,3;0) нм для области 3 и (0;0;0) нм для области 4.

Следующим шагом является решение уравнения Шредингера и нахождение комплексных волновых функций для дырок и электронов с учётом средних значений потенциала (в работе не приводятся):

(10)

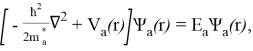
где а — тип носителя заряда, ħ — приведенная постоянная Планка, m _a — эффективная масса электрона или дырки, зависящая от радиус-вектора r, V(r) — потенциальная энергия зоны дна проводимости или потолка валентной зоны, Ѱ _a (r) — зависящая от координаты волновая функция для электронов или дырок, E _a — собственная энергия носителей заряда.

Расчёт E _a проводится по формуле для определения n -го дискретного квантового уровня для двух измерений декартовой системы координат:

(11)

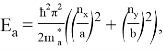
где a = b =40 нм — стороны кристаллографической ориентации в материале. показатели уровня квантования в координатных направлениях. Поскольку модель КТ сферическая, равны между собой. В рамках модели проведен расчет для первого уровня квантования, т. е. когда n _x =n _y =1 , поскольку возбуждение носителей заряда до следующих уровней требует значительного внешнего воздействия.

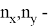
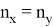
Таблица 1

Сводные значения рассчитанных параметров

F 1–2 *10– 12 , Н	F 1–3 *10– 12 , H	W 1–2 , эВ	W 1–3 , эВ	E c -E F , эВ	ρ 2 , Кл*м -2	ρ 3 , Кл*м -2	E e1 , эВ	E p1 , эВ
32	8	0,132	0,007	0,017	0,121	0,004	0,026	0,0001

На рис. 4–6 показаны результаты, полученные из решения уравнения в частных производных для энергии первого дискретного уровня. Расчеты производились методом конечных элементов с учетом рассчитанных значений потенциала в ПО и рассчитанных значений ħ ² /2m ^* _a и E _a для электронов и дырок.

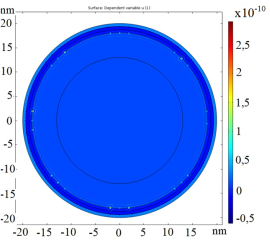
Рис. 4. Значение волновых функций для электронов с энергией первого квантового дискретного уровня в центральном сечении сферической КТ InSb с учётом хода потенциала

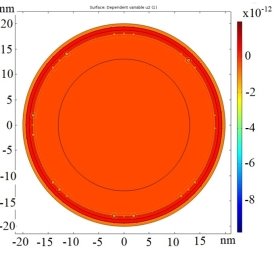
Рис. 5. Значение волновых функций для дырок с энергией первого квантового дискретного уровня в сечении сферической КТ InSb с учётом хода потенциала

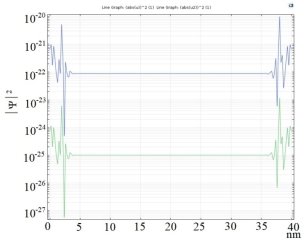
Рис. 6. График распределения электронов (синяя линия) и дырок (зелёная линия) с энергией первого квантового дискретного уровня в сечении сферической КТ InSb с учётом хода потенциала

На рис. 6 показаны графики квадратов модулей полученных волновых функций Ψ ² для электронов и дырок с энергиями первого квантового дискретного уровня. Величина демонстрируемого на графике параметра показывает вероятность нахождения носителя заряда в данной точке пространства. Показано, что дырки и электроны с большей вероятностью находятся в приповерхностных слоях КТ. Однако, значение волновой функции дырок меньше, чем у электронов — это связано с большей эффективной массой дырок в решётке антимонида индия.

Заключение

Исследовано влияние поверхностных состояний, обусловленных обрывом кристаллической решётки, на электрические свойства полупроводниковой сферической квантовой точки InSb. Построена физическая модель КТ с поверхностными состояниями и получены распределения носителей заряда в центральном сечении КТ. Анализ результатов решения уравнения Пуассона показал, что поверхностные состояния в квантовых точках могут считаться потенциальными ямами шириной, сравнимой с постоянной решётки, что резко увеличивает вероятность нахождения носителей заряда на поверхности КТ. Полученные в результате численного моделирования распределения дают основание полагать, что ПС могут создавать в КТ центры, на которых велика вероятность рекомбинации носителей заряда. Это свойство может быть использовано в прямозонных полупроводниках для создания КТ с высоким коэффициентом усиления, за счёт излучательной рекомбинации носителей заряда в центрах, создаваемых поверхностными состояниями.

Работа поддержана грантом РФФИ № 19–07–00595 А

Литература:

1. Giansante, C. Surface Traps in Colloidal Quantum Dots: A Combined Experimental and Theoretical Perspective / C. Giansante, I. Infante. // The Journal of Physical Chemistry Letters. — 2017. — № 8. — pp. 5209–5215.
2. Veamatahau, A. Origin of surface trap states in CdS quantum dots: relationship between size dependent photoluminescence and sulfur vacancy trap states / Veamatahau A., Jiang B., Seifert T., Makuta S., Latham K., Kanehara M., Teranishi T., Tachibana Y. // Phys Chem Chem Phys.. — 2015. — № 17. — pp. 2850–2858.
3. Segura-Ruiz, J. Inhomogeneous free-electron distribution in InN nanowires: Photoluminescence excitation experiments / J. Segura-Ruiz, A. Molina-Sánchez, N. Garro, A. García-Cristóbal, and A. Cantarero // Phys. Rev. B — 2010/ — № 82. — 125319.
4. Кабанов, В. Ф. Свойства квантовых точек InSb, полученных методами коллоидного синтеза и химического травления / В. Ф. Кабанов, А. И. Михайлов, М. В. Гавриков, Д. В. Крыльский. // Материалы XI Международной научно-технической конференции «Микро- и нанотехнологии в электронике». — Нальчик: КБГУ, 2019. — С. 116–120.
5. Киселев, В. Ф. Основы физики поверхности твердого тела / В. Ф. Киселев, С. Н. Козлов, А. В. Зотеев. — Москва: Изд-во Московского университета, 1999. — 284 c.
6. Пека, Г. П. Физические явления на поверхности полупроводников / Г. П. Пека. — Москва: Высшая школа, 1984. — 214 c.