The article describes the method of incremental group control ship power complexes which can be used when searching for the best fuel economy for a large group of fuel in energy converters with a variety of other types of energy.
Keywords: method of incremental control group, marine energy complex, optimum fuel consumption
Требования, предъявляемые на водном транспорте к повышению энергоэффективности динамических объектов и систем, решение проблемы энергосбережения на качественно новом уровне должны выполняться с использованием методов и средств современной теории оптимизации, математического моделирования и алгоритмизации принятия решений [1]. Метод применим к классу СЭУ, судовых энергетических комплексов и технологических объектов, служащих для преобразования энергии топлива в другие виды энергии и являющихся крупными потребителями топлива, расходные характеристики которых можно аппроксимировать квадратичными полиномами. К объектам, принадлежащим к данному классу, можно отнести установки с несколькими паровыми котлами, теплообменные установки для получения горячей воды и других энергоносителей, генераторные агрегаты судовых электростанций, автономные электростанции различного назначения. Расход топлива i-ым объектом данного класса является нелинейной функцией нагрузки, аппроксимируемой квадратичным полиномом.
![]() , i=1,2, …, n,(1)
, i=1,2, …, n,(1)
где ai, bi, ci -постоянные коэффициенты полинома,
Li — нагрузка i-ro технологического объекта,
Fi — количество топлива, потребляемого i-ым объектом на режиме, соответствующем нагрузке Li,
n — число технологических объектов в группе.
Групповое управление предусматривает параллельное подключение технологических объектов к сети, предназначенное для обеспечения спроса потребителей на энергоноситель вида Li, причем
![]() , i=1,2, …, k(2)
, i=1,2, …, k(2)
где k n — число параллельно работающих объектов в текущий момент,
L — спрос на энергоноситель, реализуемый с помощью энергетической сети.
Рассматривается случай, когда в составе группы находятся объекты с различными расходными характеристиками. Задача управления энергопотреблением формулируется следующим образом: минимизировать
![]() (3)
(3)
Путем вариации Li при соблюдении ограничения — равенства (2) и системы ограничений — неравенств вида
![]() , (4)
, (4)
где Li min, Li max — минимальное и максимальное предельные значения нагрузки i-гo объекта.
Заметим, что нагрузкой Li, для различных объектов могут быть соответствующие физические величины. Для парогенераторных агрегатов — это расход пара с заданными параметрами, судовых ДГА — мощность (активная мощность), для отопительных котлов — расход энергоносителя определенной температуры, газоперекачивающих станций — расход газа, находящегося под давлением и т. п. Выходные координаты Fi могут относиться к одному виду топлива (мазут, дизельное топливо, газ, уголь, газоконденсат и т. д.), а при использовании различных топлив — измеряться в условных топливных единицах для сохранения размерности F критерия качества (3).
Для решения приведенной выше задачи энергосбережения могут использоваться различные методы и алгоритмы оптимизации, хорошо отработанный инструментарий компьютерных вычислительных сред [2]. Вместе с тем, учитывая вид полинома (1) для энергосбережения предлагается инкрементальный метод [3]. Метод основан на поиске оптимальных решений путем построения инкрементальных функций потребления топлива [3].
Инкрементальные функции представляют собой зависимости
![]() , i = 1, 2, …, n(5)
, i = 1, 2, …, n(5)
Используя технический прием, основанный на применении множителей Лагранжа, можно показать, что оптимальный режим при групповом управлении “n” объектами обеспечивается в том случае, если инкрементальные функции равны между собой. Иначе говоря, должно выполняться условие
![]() (6)
(6)
при соблюдении ограничений (2) и (4).
Таким образом, метод инкрементальных характеристик позволяет нелинейную задачу оптимизации расхода топлива и энергии привести к модели линейного программирования. Решение в условиях ограничений предлагается выполнять по следующему алгоритму:
- Для группы «k« объектов (k=2,3,..., n), параллельно работающих на сеть, определить расходные характеристики и аппроксимировать их квадратичными полиномами (1).
- Согласно (5), получить инкрементальные функции с граничными условиями (4).
- Записать минимальные и максимальные значения инкрементальных функций и выполнить их сортировку.
- В порядке возрастания элементов вектора сортировки установить последовательность изменения нагрузки объектов как функции S, согласно формуле (6).
-
Для установленной последовательности определить критерий качества Fopt(S), спрос на энергоноситель (нагрузку сети) L(S), нагрузки технологических объектов L1(S), L2(S), …, Lk(S) как функции инкрементального значения S на интервале
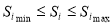 .
.
- Использовать полученные функциональные зависимости для группового управления объектами в реальном масштабе времени по схеме:
LS (L1(S), L2(S), …, Lk(S)).
Функционирование алгоритма поясним на примере параллельной работы трех судовых дизель-генераторных агрегатов (ДГА). Расходные характеристики ДГА (п.1 алгоритма) заданы в виде трех полиномов [4]:
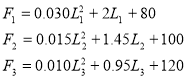
Инкрементальные функции (п.2) определим с помощью уравнений (5):
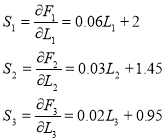
Согласно (4), граничные условия (максимальные и минимальные мощности генераторных агрегатов):
L1min = 0, L1max = 50 кВт,
L2min = 0, L2max = 70кВт,
L3min = 0, L3mах = 80 кВт.
Максимальные и минимальные значения инкрементальных функций представим в виде вектора: R = [S3minS2minS1minS3maxS2maxS1max], который после выполнения операции сортировки равен [0.95 1.45 2.00 2.55 3.55 5.00].
Для выполнения п.4 алгоритма произведем построение инкрементальных функций, и представим их на рис. 1.
Последовательность изменения нагрузки группы объектов в зависимости от спроса определяется элементами вектора R. Согласно рис. 1, при изменении инкремента на интервале 0.95 S < 1.45 необходимо изменять только мощность третьего генератора. На интервале 1.45 S < 2 должны работать на сеть второй и третий генераторы при соблюдении условия S2 = S3.
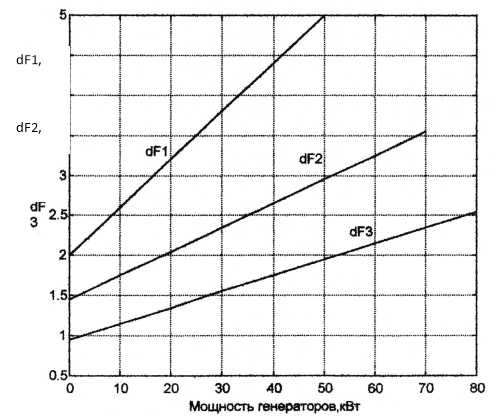
Рис. 1. Инкрементальные характеристики генераторов
На интервале 2 S < 2.55 нагрузка должна распределяться между тремя ДГА, причем минимальному расхода топлива (минимуму критерия качества) будет соответствовать условие распределения: S1 = S2 = S3.
С момента достижения максимальной нагрузки третьего генератора L3max и до достижения максимальной мощности второго генератора L2max, рабочий интервал (2.55 S < 3.55), мощность L3max = const, а значения L1 и L2 следует изменять при соблюдении равенства S1 = S2. Наконец, на последнем рабочем интервале (3.55 S 5.0), согласно рис. 1 необходимо поддерживать L3max, L2max постоянными. Увеличение спроса L должно обеспечиваться только за счет возрастания мощности первого генератора.
По приведенному выше алгоритму были выполнены вычисления, результаты которых изображены в виде графиков, представленных на рис. 2.
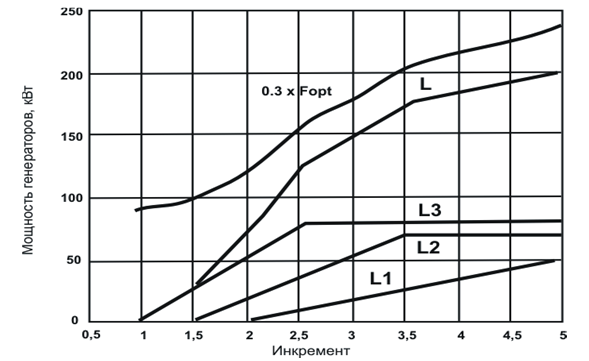
Рис. 2. Оптимальные режимы при групповом управлении генераторными агрегатами
В составленной машинной программе величина S = 0.01, и расчетные значения (п.5 алгоритма) для всех координат получены в виде матрицы размерности (6406). Отметим, что элементам вектора R соответствуют столбцы этой матрицы с номерами 1, 51, 106, 161, 261 и 406. Ниже приведены «вырезки» из матрицы, соответствующие перечисленным столбцам.
>>Optim
Optim=
|
300.0000 |
330.0000 |
409.0625 |
534.1875 |
686.6875 |
790.0000 |
|
0 |
25.0000 |
52.5000 |
80.0000 |
80.0000 |
80.0000 |
|
0 |
0 |
18.3333 |
36.6667 |
70.0000 |
70.0000 |
|
0 |
0 |
0 |
9.1667 |
25.8333 |
50.0000 |
|
0 |
25.0000 |
70.8333 |
125.8333 |
175.8333 |
200.0000 |
|
0.9500 |
1.4500 |
2.0000 |
2.5500 |
3.5500 |
5.0000 |
В первой «Optim» строке приводятся значения минимума критерия качества (4), во второй — мощность третьего генератора, в третьей — второго генератора, в четвертой строке — мощность первого генератора. В пятой строке «Optim» приведена нагрузка сети. Наконец, в шестой строке выведены S в точках переключения с режима на режим при инкрементальном групповом управлении генераторными агрегатами.
В заключение следует отметить, что полученные расчетные значения во всех рабочих точках идентичны результатам вычислений, выполненных методом динамического программирования. В отличие от других методов оптимизации, метод инкрементальных характеристик для рассматриваемого класса объектов обладает достаточной простотой и наглядностью при использовании графических построений.
Эффективность предложенного алгоритма особенно высока при наличии большого числа управляемых объектов, для работы которых могут использоваться различные виды топлива. Работа двигателей на тяжелых сортах топлива приводит к снижению общих расходов дизельного топлива, которое оценивается в терминах оценки экономии светлых нефтепродуктов. Сокращение расходов дизельного топлива обеспечивается за счет применения, например, газотурбинного топлива, стоимость которого меньше дизельного. Применение двухтопливных систем и средств топливоподготовки дает возможность использовать на судах моторное топливо, а также различные топливные смеси. В этих условиях коэффициенты уравнений (1) и (5) должны изменяться в зависимости от конкретной ситуации топливоиспользования. Следовательно, оперативно должны корректироваться оптимальные режимы энергосбережения объектов-потребителей топлива и энергии.
Необходимо отметить, что практическая реализация оптимальных режимов имеет определенные особенности, состоящие в том, что за основу приняты статические характеристики объектов. Таким образом, нагрузка энергетической сети предполагается квазистационарной или, по крайней мере, время переходных процессов в сравнении с суммарным временем функционирования объектов является малым, и им можно пренебречь.
В действительности каждый генераторный агрегат является сложным динамическим объектом с автономными регуляторами частоты вращения, напряжения сети, устройствами для параллельной работы, синхронизации. При параллельной работе ДГА динамические свойства системы существенно усложняются, а оптимизация в переходном режиме и, следовательно, перераспределение нагрузки с высоким быстродействием с целью уменьшения динамической ошибки может привести к ухудшению робастных свойств системы [5]. В частности, усиление колебательных свойств может привести к управлению, не отвечающему экономии топлива по условиям неравновесной термодинамики.
Для повышения эффективности управления энергосбережением в таких случаях целесообразно при перераспределении нагрузки реализовать режим сглаживания, который должен исключать большие приращения корректирующего сигнала по оптимизационному каналу передачи информации. Быстродействие может быть снижено за счет последовательности ступеней с малой амплитудой, генерируемых периодически с момента изменения полной нагрузи на сеть.
Предполагается, что существующая штатная система работает в более высоком диапазоне частот, а контур оптимального распределения нагрузки «корректирует» режим работы в низкочастотном диапазоне. Тем самым исключается реакция на случайные кратковременные возмущения, а оптимизация осуществляется по средним значениям полной нагрузки на заданном временном интервале. В таком режиме контур оптимизации энергосбережения практически не влияет на устойчивость и качество управления, обеспечиваемого системами.
При работе контура оптимального энергосбережения в режиме «сглаживания» снижаются требования к производительности судового вычислительного комплекса. Последовательность формирования управляющих воздействий при групповом управлении генераторными агрегатами должна определяться по следующему правилу: в переходном режиме, если нагрузка сети возрастает, необходимо сначала загружать генераторы, имеющие инкрементальные характеристики с наименьшим наклоном; в случае уменьшения нагрузи, следует сначала разгружать генераторы, инкрементальные характеристики которых имеют наибольший наклон.
В части, касающейся перспективы использования метода инкрементального группового управления энергосбережением, следует отметить следующее. Метод инкрементального группового управления наиболее эффективен при поиске оптимальных расходов топлива для большой группы преобразователей энергии топлива в другие виды с различными энергоносителями. Например, на плавучих буровых платформах, работающих в прибрежных водах, могут использоваться генераторные агрегаты, число которых составляет 1216 (с различными расходными характеристиками).
Литература:
- Resolution MEPC.214(63). 2012 guidelines on survey and certification of the energy efficiency design index (EEDI).
- Компьютерные технологии обработки информации / Под ред. С. В. Назарова — М.: “Финансы и статистика”, 1995.- 248 c.
- Королёв В.И, Сахаров В. В. Экономия топлива при групповом управления одним классом объектов / В сб. науч. тр. СПГУВК «Методы прикладной математики в транспортных системах». — СПб., 2002. — Вып. 6. — С. 119–124.
- Бурков В. Н., Ирикова В. А. “Модели и методы управления организационными структурами”. М: Наука, 1994. С.91–126.
- Тормашев Д. С., Сахаров В. В., Кузьмин А. А., Чертков А. А. Сплайн — метод экономического управления расходом топлива на речных судах. М.: Речной транспорт (XXI век). 2014. — № 3 (68), с. 62–65.

