В статье рассмотрен комплекс задач по энергоснабжению и эффективному финансированию проектов энергетики, учитывающие ограничения в производстве, потреблении и доставки энергоресурсов. Показано, что задачи оптимизации энергоснабжения по критерию минимум затрат могут быть формализованы на языке линейного программирования, в виде задачи транспортного типа или задачи о назначениях.
Ключевые слова: энергоресурсы, математические модели, энергоаудит, линейное программирование
В современном мире необходимым условием сохранения жизни и развития цивилизации стало обеспечение человечества достаточным количеством энергии и топлива. Энергетика, в широком смысле, охватывает сложную совокупность процессов преобразования и передачи энергии от источников получения природных энергетических ресурсов до приемников энергии включительно [8].
Энергетика представляет собой сложный развивающийся объект, исследование которого возможно только на основе системного подхода. Важная особенность энергетики — ее развитие в направлении углубления принципа системности, т. е. по пути формирования совокупности больших систем на основе сочетания концентрации как производства, так и средств транспорта преобразованных видов энергии и энергетических ресурсов, и централизации их распределения [4,5].
Главное в развитии систем энергетики — глобальность, характеризуемая превращением их в единые системы. Перед тем, как разработать и назначить необходимые меры для обеспечения успешного внедрения комплекса мер по оптимизации энергоснабжения больших систем, проводят энергоаудит [6,9].
Энергетическое обследование — сбор информации об использовании энергетических ресурсов, показателях энергетической эффективности. Энергоаудит помогает грамотно применить существующие задачи и оптимизировать их [7]. Также от ритмичности и бесперебойности энергоснабжения предприятия зависит достижение планируемых экономических показателей, от себестоимости получения и распределения различных видов энергии зависит себестоимость выпускаемой предприятием продукции.
Для комплексных задач энергетики, часто тесно связанных с ними смежных народнохозяйственных задач, важен системный подход за счет оптимизации и разработки комплекса задач [3,4]. Для достижения цели разработана математическая постановка нижеописанных задач.
1. Комплекс задач по оптимизации процесса энергоснабжения предприятий.
Задача внешнего энергоснабжения при планировании перевозок однородных энергоносителей (угль, торф, газ, нефть) между поставщиками и потребителями, размещенными в различных точках пространства. Постановка задачи заключается в следующем.
Пусть имеется m пунктов производства (поставщиков) некоторого однородного продукта энергоносителя и n пунктов его потребления. Для каждого пункта производств i известен объем производств ![]()
![]() , а для каждого пункта потребления j-объем потребления
, а для каждого пункта потребления j-объем потребления ![]() , при этом чаще всего предполагается, что суммарные производств и суммарное потребление сбалансированы, т.е.
, при этом чаще всего предполагается, что суммарные производств и суммарное потребление сбалансированы, т.е.
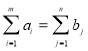
где ![]() - пункт производства энергоносителя;
- пункт производства энергоносителя;![]() -объем производства энергоносителя;j -пункт потребления энергоносителя;
-объем производства энергоносителя;j -пункт потребления энергоносителя; ![]() - объем потребления энергоносителя.
- объем потребления энергоносителя.
Задача затраты ![]() на перевозку единицы энергоносителя от каждого пункта производства до каждого пункта потребления. Требуется составить план перевозок, отслеживающий всех потребителей, не выводящий за пределы производительности поставщиков и отслеживающий минимум суммарных затрат на перевозку.
на перевозку единицы энергоносителя от каждого пункта производства до каждого пункта потребления. Требуется составить план перевозок, отслеживающий всех потребителей, не выводящий за пределы производительности поставщиков и отслеживающий минимум суммарных затрат на перевозку.
Ведением переменных![]() , представляющих собой объемы перевозок от каждого поставщика к каждому потребителю j, эта задача приводится к минимуму пути:
, представляющих собой объемы перевозок от каждого поставщика к каждому потребителю j, эта задача приводится к минимуму пути:
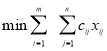 ,(1)
,(1)
при условиях:
![]()
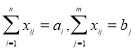 где
где ![]() =
=![]() , j=
, j=![]() .(2)
.(2)
Данная задача решает проблему экономичного плана транспорта однородных или взаимозаменяемых продуктов из пунктов производства (источников теплоты) в пункты потребления (абонентские установки потребителей теплоты) и является задачей линейного программирования транспортного типа. Наиболее распространенным методом ее решения является «метод потенциалов» [1,3].
2. Задача внутреннего энергоснабжения при планировании экономного назначения источников тепло (электро) энергии на потребителей. Постановка задачи заключается в следующем.
Пусть имеется n источников энергии и n потребителей энергии внутри некоторого производственного помещения (Объекта). При закреплении i-го источника за j-ым потребителем производятся затраты ![]() , i,j =
, i,j = ![]() . Накладываются ограничения: каждый источник может прикрепляться только к одному потребителю; каждый потребитель может прикрепляться только к одному источнику. Требуется в рамках данных ограничений найти такую схему закрепления потребителей за источниками при которой достигаются минимальные суммарные затраты на сопряжение теплоносителями источника с потребителями.
. Накладываются ограничения: каждый источник может прикрепляться только к одному потребителю; каждый потребитель может прикрепляться только к одному источнику. Требуется в рамках данных ограничений найти такую схему закрепления потребителей за источниками при которой достигаются минимальные суммарные затраты на сопряжение теплоносителями источника с потребителями.
Введем переменную ![]() - признак назначения источника энергии на потребителя энергии
- признак назначения источника энергии на потребителя энергии
![]() =
=![]()
![]() ,
,
тогда математически задача формируется следующим образом
![]()
![]() ,
,![]() (3)
(3)
при ограничениях:
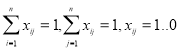 .
.![]() (4)
(4)
Выражение (3) означает цель решения задачи, а выражение (4) соответствует ограничениям.
Данная задача является задачей целочисленного линейного программирования наиболее распространенным методом ее решения является «Венгерский метод» [1].
3. Задача финансирования исследовательских проектов при разработке систем энергоснабжения. Постановка задачи заключается в следующем.
Пусть на протяжении T лет возможно осуществление n- исследовательских проектов. Ожидаемый эффект каждого j-го проекта выраженный в единицах полезности составляет ![]() ,
, ![]() . Затраты в год i на осуществление проекта составляют
. Затраты в год i на осуществление проекта составляют ![]() , а общий лимит капиталовложений на исследования в году i равен
, а общий лимит капиталовложений на исследования в году i равен ![]() ,
,![]() .Требуется указать максимально эффективный набор проектов не выходящий за пределы отпускаемых вложений.
.Требуется указать максимально эффективный набор проектов не выходящий за пределы отпускаемых вложений.
Введем переменную ![]()
![]() =
=![]() ,
,
найти
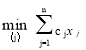 , (5)
, (5)
при ограничениях
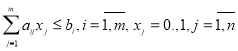 . (6)
. (6)
Задача является задачей нелинейного целочисленного программирования типа «задача о ранце». Метод решения «метод ветвей и границ» [2].
В статье показано, что задачи оптимизации схем энергоснабжения [10] по критерию минимум затрат могут быть формализованы на языке линейного программирования, в виде задачи транспортного типа или задачи о назначениях.
В настоящее время разработаны эффективные методы их решения — метод потенциалов, венгерский метод, метод ветвей и границ. Создана библиотека программ, позволяющие находить точные решения рассмотренных оптимизационных задач. В результате разработана схема обеспечения энергоресурсами по критерию минимальных затрат на их доставку и финансирование, при ограничениях на объемы производства и потребления.
Литература:
- Кузнецов, Ю. Н. Математическое программирование: Учебник / Ю. Н. Кузнецов, В. И. Кузубов А. Б., Волощенко. Изд-во Вычшая школа)- 2-е изд, 1980. — 302с.
- Кофман,А.Методыи моделиисследованияопераций / А. Кофман, А. Анри-Лабордер — Изд-во: «Мир», 1977. — 432с.
- Соболь, Б. В. Методы оптимизации: практикум / Б. В. Соболь, Б. Ч. Месхи, Г. И. Каныгин. — Ростов н/Д.: Феникс, 2009. — 380с.
- Комплексное развитие систем коммунальной инфраструктуры муниципального образования: монография / В. Н. Семенов [и др.]. Изд-во Воронежского ГАСУ, 2010. — 135с.
- Китаев, Д. Н. Развитие системы теплоснабжения городского округа город Воронеж в долгосрочной перспективе / Д. Н. Китаев // Инженерные системы и сооружения. — 2010. — № 2(3). — С.72–77.
- Семенов, В. Н. Энергосбережение и повышение энергоэффективности для объектов социальной сферы / В. Н. Семенов, Д. Н. Китаев, Т. В. Щукина, Д. Ю. Королев // Энергосбережение. — 2010. — № 6. — С. 38–43.
- Китаев, Д. Н. Современные отопительные приборы и система теплоснабжения /Д. Н. Китаев, Т. В. Щукина. — 2012. — № 6. — С.59–62.
- Семенов, В. Н. Актуальные проблемы теплоснабжения муниципальных образований (на примере городского округа город Воронеж) / В. Н. Семенов, Д. Н. Китаев, А. С. Овсянников // Вестник центрального территориального отделения Российской академии архитектуры и строительства. — 2015. — Вып.14. — С.100–108.
- Китаев, Д. Н. Расчет температуры наружного воздуха в точке излома температурного графика / Д. Н. Китаев // Новости теплоснабжения. — 2012. — № 10. — С.46–48.
- Китаев, Д. Н. Перспективные схемы использования когенерационных установок в системах теплоснабжения /Д. Н. Китаев, А. В. Золотарев, Н. С. Шестых // Инженерные системы и сооружения. — 2012. — № 2. — С. 26–29.

