Введение
При численном решении задачи Коши для систем обыкновенных дифференциальных уравнений вида
![]() (1)
(1)
в [1–2] предлагается применять явные методы типа Рунге-Кутты
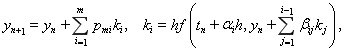 (2)
(2)
где y и f – гладкие вещественные N-мерные вектор функции; t – независимая переменная; ki, 1≤i≤m – стадии метода; αi, pmi, βij, 1≤i≤m, 1≤j≤i-1 – коэффициенты, определяющие свойства точности и устойчивости схемы (2). Тем не менее, при интегрировании жестких задач условие устойчивости накладывает сильные ограничения на величину шага интегрирования, что существенно снижает эффективность метода.
В [2–3] построен алгоритм получения коэффициентов многочленов устойчивости, с помощью которых можно построить явные методы с заданными формой и размером области устойчивости до степени m=13. Там же численно показано значительное повышение эффективности алгоритмов интегрирования за счет комбинирования численных формул с различными характеристиками устойчивости в процессе вычислений на основании критерия устойчивости. При этом в [2] не рассмотрен вопрос о выборе коэффициентов βij, которые влияют на устойчивость промежуточных численных схем и, в конечном счете, на эффективность алгоритма интегрирования. Авторы ограничились замечанием, что устойчивости промежуточных формул можно добиться за счет выбора достаточно малых βij.
Здесь на основе алгоритма, описанного в [4], получены коэффициенты многочленов устойчивости до степени m=27, соответствующие методам первого порядка точности с максимальным интервалом устойчивости. Предложен такой выбор коэффициентов βij, чтобы промежуточные численные схемы метода были согласованы с основной. Построены методы первого порядка с согласованными областями устойчивости, и приведены результаты расчетов.
Численные схемы
Для упрощения выкладок далее рассмотрим задачу Коши для автономной системы обыкновенных дифференциальных уравнений
![]() (3)
(3)
для решения которой применим методы типа Рунге-Кутты, записанные в следующем виде
![]() (4)
(4)
где ki=hf(yn,i-1), 1≤i≤m, yn,0= yn. Все полученные ниже результаты можно использовать для неавтономных задач, если в (2) положить
![]() (5)
(5)
В дальнейшем потребуется матрица Bm с элементами bij следующего вида [2]:
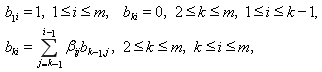 (6)
(6)
где βij – коэффициенты схемы (2) или (4).
Устойчивость одношаговых методов обычно исследуется на линейном скалярном уравнении
![]() (7)
(7)
с комплексным λ, Re(λ)<0. Применяя вторую формулу (4) к (7), получим
![]() (8)
(8)
Обозначая Cm=(cm1, …, cmm)T и Pm=(pm1, …, pmm)T, соотношения (8) можно переписать в виде
![]() (9)
(9)
где элементы матрицы Bm определены соотношениями (6). Для промежуточных численных схем (4) имеем
![]() (10)
(10)
Используя обозначения βk=(βk+1,1, …, βk+1,k)T и ck=(ck1, …, ckk)T, получим, что коэффициенты βij промежуточных схем (4) и коэффициенты соответствующих многочленов устойчивости связаны соотношениями
![]() (11)
(11)
Заметим, что из сравнения (6) и (10) следует, что bki = ci-1,k-1, то есть элементы (k+1)‑го столбца матрицы Bm совпадают с коэффициентами многочлена устойчивости Qk(z). Отсюда следует, что при заданных коэффициентах многочленов устойчивости основной и промежуточной численных схем коэффициенты методов (4) однозначно определяются из линейных систем (9) и (11) с верхними треугольными матрицами Bi, 1≤i≤m. Ниже этот факт будет использоваться при определении коэффициентов численных формул (4) при условии, что области устойчивости промежуточных численных схем согласованы с основной.
Разлагая точное и приближенное решения в ряды Тейлора по степеням h, можно записать
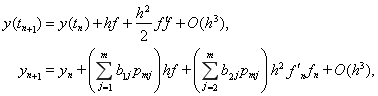 (12)
(12)
где элементарные дифференциалы вычислены на точном y(tn) и приближенном yn решениях, соответственно. Из сравнения соотношений (12) видно, что численная формула (4) будет иметь первый порядок точности, если ![]() . Отсюда следует, что для построения m-стадийных методов первого порядка точности в линейной системе (9) следует положить cm1=1.
. Отсюда следует, что для построения m-стадийных методов первого порядка точности в линейной системе (9) следует положить cm1=1.
Согласование областей устойчивости
Предположим, что заданы коэффициенты многочленов устойчивости
![]() (13)
(13)
При выборе коэффициентов многочлена (13) можно руководствоваться различными соображениями. Если выбрать многочлен Чебышева, то соответствующий метод будет иметь максимальную длину области устойчивости вдоль вещественной оси. Область устойчивости таких методов является почти многосвязной и в результате ошибок округлений, которые приводят к появлению небольших мнимых частей собственных чисел матрицы Якоби, она сокращается. Описанным в [4] способом выберем коэффициенты многочлена таким образом, чтобы область устойчивости растягивалась вдоль мнимой оси и становилась односвязной. Это обеспечивает лучшие свойства устойчивости метода к ошибкам округления при несущественном сокращении длины интервала устойчивости.
Для каждого k, 1≤k≤m, обозначим через γk длину такого максимального интервала [γk,0], что для всех z∈[γk,0] имеет место неравенство |Qk(z)| ≤1. Учитывая, что z=hλ, в (13) для каждого Qk(z), 1≤k≤m проведем замену h на (hγk/γm). В результате вместо (13) получим
![]() (14)
(14)
Замена h на (hγk/γk) означает, что приближенное решение по промежуточным схемам (4) вместо точек (tn+ck1h), 1≤k≤m-1 будет вычисляться в точках (tn+c'k1h), 1≤k≤m-1. В этом случае максимальный шаг из условия устойчивости основной схемы будет максимальным и для промежуточных численных формул.
Определение коэффициентов методов (4) будем осуществлять по следующему алгоритму. С использованием [1] вычислим коэффициенты полиномов (13), удовлетворяющие некоторым заданным свойствам. Затем вычислим коэффициенты многочленов (14) с применением соответствующей замены переменных. Учитывая, что элементы (k+1)-го столбца матрицы Bm совпадают с коэффициентами многочлена устойчивости Q'k(z), сформируем матрицу
 (15)
(15)
Используя в (11) вектор c'k=(c'k1, …, c'kk)T вместо ck, все коэффициенты методов (4) с согласованными областями устойчивости однозначно определяются из линейных систем (9) и (11).
Контроль точности вычислений
Для контроля точности методов первого порядка будем использовать оценку локальной ошибки δn,1. С применением (12) видим, что для m-стадийного метода она имеет вид
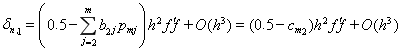 ,
,
где cm2 – коэффициент при z2 многочлена устойчивости (8). Оценку εn,1 данной ошибки можно вычислить многими способами. Разлагая ki, 1≤k≤m в ряды Тейлора, нетрудно видеть, что
![]()
Отсюда следует, что εn,1 можно вычислить по приближенной формуле
![]() (16)
(16)
Для жестких задач на переходных участках характерным является быстрое изменение решения на небольших промежутках. Для того чтобы избежать неудовлетворительной точности, естественно, в оценке ошибки использовать стадии, вычисленные в крайних точках отрезка [tn,tn+1]. Стадия k1 вычисляется в точке tn, и поэтому в (16) положим j=1, i>j. Для методов с согласованными областями устойчивости имеет место неравенство α1 < α2 <…< αm < 1. Отсюда следует, что ни одна стадия в точке tn+1 не вычисляется. С другой стороны, применение в (16) стадий с достаточно большими номерами будет приводить к значительному увеличению вычислительных затрат в случае повторных вычислений решения вследствие невыполнения требуемой точности. С целью повышения эффективности расчетов поступим следующим образом. В качестве предварительной оценки применим величину
![]() (17)
(17)
Поскольку k1 зависит от размера шага линейно, то нарушение неравенства ||ε'n,1|| ≤ ε будет приводить всего лишь к одному дополнительному вычислению правой части задачи (3). Здесь ε – требуемая точность расчетов, ||·|| – некоторая норма в RN. Учитывая, что
![]() ,
,
окончательное решение по точности будем принимать на основе неравенства ||ε''n,1||≤ε, где
![]() .(18)
.(18)
Контроль устойчивости
Неравенство для контроля устойчивости построим по аналогии с [1]. Для получения данного неравенства применим метод (4) для решения задачи (3) при f(y)=Ay+b, где A и b соответственно матрица и вектор с постоянными коэффициентами размерности N. Очевидно, что в этом случае выполнены соотношения
![]() ,
,
где fn=Ayn+b, f'n=A. Выберем b'i и b''i, 1 ≤ i ≤ 3 из условия выполнения равенств
![]()
Нетрудно видеть, что данные соотношения будут выполнены, если
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
Теперь оценку максимального собственного числа λnmax матрицы Якоби ∂f(yn)/∂y задачи (3) можно вычислить по формуле
![]() (19)
(19)
Тогда неравенство для контроля устойчивости m-стадийного метода (4) имеет вид hλnmax≤| γm|, где |γm| – длина интервала устойчивости m-стадийной схемы.
Метод первого порядка
Для численного решения задачи Коши (1) рассмотрим явный трехстадийный метод типа Рунге-Кутты вида
![]()
![]()
![]() (20)
(20)
где y и f – вещественные N-мерные вектор-функции; t – независимая переменная; h – шаг интегрирования; k1, k2 и k3 – стадии метода; p1, p2, p3, β21, β31, β32 – числовые коэффициенты, определяющие свойства точности и устойчивости (20).
Выберем коэффициенты (20) таким образом, чтобы они имели первый порядок точности и расширенную область устойчивости. Если рассматривать методы с максимальной областью устойчивости, то она является многосвязной. Построим многочлены первой, второй и третьей степени такие, чтобы соответствующие методы имели односвязные области устойчивости с интервалом устойчивости, близким к максимальному. Применяя алгоритм [4], получим коэффициенты
![]() ,
,
![]() ,
,
![]() .
.
При этом
![]() .
.
Составив и решив линейные системы (9) и (11) с учетом (15) для схемы (20), получим в результате коэффициенты метода
![]() ,
,
![]() .
.
Для контроля точности численной формулы используем оценки (17) и (18). Интервал устойчивости численной схемы (20) первого порядка точности равен 17.46. Поэтому для ее контроля можно применять неравенство hλnmax≤17.46, где hλnmax определяется по формуле (19).
Результаты расчетов
Расчеты проводились с точностью ε=10-2 на Intel(R) Core(TM) i3-5010U CPU с двойной точностью. В конкретных расчетах норма ||ξ|| в неравенствах для контроля точности вычисляется по формуле
![]() ,
,
где i – номер компоненты, r – положительный параметр. Если по i-й компоненте решения выполняется неравенство |yin|<r< em="">, то контролируется абсолютная ошибка rε, в противном случае – относительная ошибка ε. В расчетах параметр r выбирался таким образом, чтобы по всем компонентам решения фактическая точность была не хуже задаваемой. </r<>
Сравнение эффективности метода Рунге-Кутта первого порядка с согласованными областями устойчивости с контролем точности и устойчивости проводилось с трехстадийным методом третьего порядка точности с контролем и без контроля устойчивости, описанным в [5]. Ниже через is, iw и if обозначены, соответственно, суммарное число шагов интегрирования, число повторных вычислений решения (возвратов), вследствие нарушения требуемой точности расчетов, и число вычислений правой части задачи (1).
В качестве тестового примера выбрана упрощенная модель с периодическим решением для описания реакции Белоусова-Жаботинского (орегонатор), которая записывается следующим образом:
![]() ,
,
![]() ,
, ![]() ,
,
![]()
Она является «слишком» жесткой для явных методов. Тем не менее, данный пример приведен здесь с целью подчеркнуть преимущество методов с контролем устойчивости.
Методом первого порядка с согласованными областями устойчивости и контролем точности и устойчивости решение задачи вычислено с затратами is=451 689, iw=1 941 и if=1 808 907. Для метода третьего порядка без контроля устойчивости затраты is=2 903 722, iw=769 200 и if=10 249 566. Из сравнения результатов следует, что контроль устойчивости приводит к повышению эффективности за счет устранения некоторых повторных вычислений решения из-за неустойчивости численной формулы. Тенденция сохраняется при интегрировании других примеров.
Заключение
В работе получены коэффициенты многочленов устойчивости до степени m = 27 и построены соответствующие явные m-стадийные методы типа Рунге-Кутты первого порядка точности, у которых области устойчивости промежуточных численных формул согласованы с областью основной схемы. Построены неравенства для контроля точности вычислений и устойчивости численной схемы.
Разработанные наборы методов первого порядка с контролем точности и устойчивости могут быть применены в алгоритмах интегрирования с переменным шагом, порядком и переменным числом стадий. В этом случае повышение эффективности достигается не только за счет переключения с метода высокого порядка на метод низкого порядка на участке установления, но и за счет «разгона» шага на этом участке путем применения набора методов первого порядка с согласованными областями устойчивости. При этом согласование численных схем приводит примерно к 30-процентному повышению эффективности алгоритма интегрирования и обеспечивает более оправданное поведение шага на участке установления.
Работа выполнена при финансовой поддержке РФФИ (проект 14-01-00047).
Литература:
1. Хайрер Э., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Жесткие и дифференциально-алгебраические задачи. – М.: Мир, 1999. – 685 с.
2. Новиков Е.А. Явные методы для жестких систем. – Новосибирск: Наука, 1997. – 195 с.
3. Новиков Е.А. Конструирование областей устойчивости явных методов типа Рунге-Кутты // Вычислительные методы и программирование. – 2009. – № 10. – С. 248–257.
4. Новиков Е.А., Рыбков М.В. Численный алгоритм построения многочленов устойчивости методов первого порядка // Вестник Бурятского государственного университета. – 2014. – № 9-2. – С. 80–85.
5. Новиков А.Е., Новиков Е.А. Комбинированный алгоритм третьего порядка для решения жестких задач // Вычислительные технологии. – 2011. – Т. 16, № 6. – С. 54–67.

