Разработаны алгоритмы получения матрицы жесткости объемного конечного элемента, поперечное сечение которого является треугольником. Произвольная точка треугольника с узлами, обозначенными латинскими буквами i, j, k, определяется координатами r и z. Для выполнения численного интегрирования треугольник с узловыми координатами ri, rj, rk, zi, zj, zk отображается на прямоугольный треугольник, локальные координаты которого ξ и η изменяются от нуля до единицы.
Связь между глобальными координатами r, z и локальными координатами ξ, η определяется линейными соотношениями
![]() ;
;![]() .(1)
.(1)
Дифференцированием (1) определяются соответствующие производные.
Разработаны алгоритмы получения матриц жесткости треугольного конечного элемента в трех вариантах.
- Компоненты вектора узловых неизвестных принимаются в виде перемещений, а гидростатическое давление считается постоянным по площади четырехугольника, состоящего из двух треугольников.
Каждая составляющая вектора перемещения внутренней точки конечного элемента аппроксимируется через узловые неизвестные линейными соотношениями (1)
![]() ;
;![]() ,(2)
,(2)
где
![]() ;
;![]() — матрицы-строки узловых неизвестных.
— матрицы-строки узловых неизвестных.
- Компонентами вектора узловых неизвестных принимаются перемещения и их первые производные
![]() ;
;
![]() .(3)
.(3)
Для аппроксимации полей перемещений внутренних точек треугольного конечного элемента через узловые неизвестные используются выражения
![]() ;
; ![]() ,(4)
,(4)
где
![]() .
.
Функции формы Gi(ξ,η имеют вид
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .(5)
.(5)
Гидростатическое давление принималось постоянным по площади четырехугольника, состоящего из двух треугольников.
-
В третьем варианте перемещения аппроксимировались соотношениями (4), а гидростатическое давление считалось изменяющимся по линейному закону в зависимости от вектора узловых значений
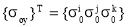 .
.
Модифицированные матрицы жесткости треугольного конечного элемента имеют размеры: 7×7 — в первом варианте конечного элемента; 19×19 — во втором варианте и 21×21 — в третьем.
В качестве примера определено напряженно-дефромированное состояние цилиндрической оболочки, рассмотренной в третьей главе. Использовался объемный конечный элемент с треугольным сечением в двух вариантах.
- В первом варианте за узловые неизвестные конечного элемента принимались перемещения, а гидростатическое давление считалось постоянным по площади четырехугольника, состоящего из двух треугольников.
- Во втором варианте расчета исследовался треугольный элемент с узловыми неизвестными в виде перемещений, их первых производных и гидростатического давления. Гидростатическое давление изменялось по площади треугольника по линейному закону.
Анализ численных результатов показал хорошую сходимость вычислительного процесса и практическое совпадение с результатами, полученными при использовании объемных конечных элементов с поперечным сечением в виде четырехугольника.
Литература:
- Оден Дж. Конечные элементы в нелинейной механике сплошных сред/ Оден Дж. Пер. с англ.- М.: Мир, 1976.- 464 с.
- Самуль В. И. Основы теории упругости и пластичности/ Самуль В. И. — М.: «Высшая школа, 1970.- 288 с.
- Постнов В. А., Хархурим И. Я. Метод конечных элементов в расчетах судовых конструкций/ Постнов В. А., Хархурим И. Я. -Л.: Судостроение, 1974, 344 с

