В математике и ее приложениях постоянно приходится иметь дело с приближенными представлениями функций. Классическими аппаратами таких представлений являются многочлены и рациональные дроби.

Пусть даны пары , .

Проблема интерполирования состоит в нахождении функции такой, что

(),

и интерполирует в узлах. Говорят о полиномиальном интерполировании, если является алгебраическим полиномом, тригонометрической аппроксимации, если — тригонометрический полином, или кусочно-полиномиальной интерполяции (или сплайн-интерполяции), если является только локально полиномиальным.

Задача полиномиальной интерполяции — найти полином , называемый интерполяционным полиномом, такой, что

.

Точки называются узлами интерполяции.

Многочлены обладают рядом недостатков, как аппарат приближения для функций с особенностями и функций с не слишком большой гладкостью.

В этой работе рассматривается постановка задачидля построения интерполирования в пространстве Соболева непериодических функций, у которых обобщенные производные порядка интегрируемы с квадратом.

Значение

ошибки интерполяционной формулы в некоторой точке есть функционал над классом функцией :

(1)

где

(2)

функционал погрешности интерполяционной формулы , – коэффициенты, а –узлы интерполяционной формулы (1), , –дельта-функция Дирака, .

Коэффициенты связаны линейными условиями

(3)

Функционал -ограниченныйи линейный в пространстве , а его норма определяется равенством

Следовательно, оценка погрешности интерполяционной формулы на функциях пространства сводится к нахождению нормы функционала (2) в сопряженном пространстве .

Итак, для оценки погрешности интерполяционной формулы (1) достаточно решить следующую задачу.

Задача 1. Найти норму функционала погрешности рассматриваемой интерполяционной формулы .

Эта задача решается в случае, когда существует так называемая экстремальная функция интерполяционной формулы, т. е. такая функция , для которой выполняется следующее равенство

Очевидно, что норма функционала погрешности зависит от коэффициентов и узлов .

Если

,(4)

тогда функционал называетсяоптимальнымфункционалом погрешности, а соответствующуюая интерполяционная формула–оптимальной интерполяционной формулой.

Таким образом для того чтобы построить оптимальную интерполяционную формулу надо решить следующую задачу

Задача 2.Найти такие значения и , чтобы выполнялось равенство (4).

и соответсвенно называются оптимальными коэффици-ентами и оптимальными узламиинтерполяционной формулы (2.1).

Литература:

1. Соболев С. Л. Введение в теорию кубатурных формул. -М.: Наука, 1974.-808 с.
2. Шадиметов Х. М. Оптимальные решетчатые квадратурные и кубатурные формулы в пространствах Соболева. Дис. докт. физ.-мат. наук. -Ташкент, 2002. -218 с.
3. Хаётов А. Р. Об оптимальных интерполяционных формулах в пространстве 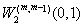// Узб. матем. журн. –Ташкент, 2010. № 2. -С. 173–179.