Одним из важнейших разделов современной общей топологии является теория кардинальнозначных инвариантов топологических пространств. Среди этих инвариантов вторым по значимости является плотность. В определяемой плотностью иерархии пространств центральное место занимают пространства наименьшей бесконечной плотности, т. е. пространства, которые содержат счетные всюду плотные подпространства. Исторически сложилось так, что эти пространства называются сепарабельными, Хотя слово «сепарабельный» в буквальном переводе означает «отделимый и непосредственного отношения к плотности не имеет. Сепарабельные пространства играют видную роль не только и общей топологии, но и в других разделах математики, где возникают топологические пространства как инструмент или объект исследований. Наличие счетного плотного множества в данном топологическом пространстве зачастую позволяет получить дополнительную информацию об этом пространстве. Так сепарабельное метризуемое пространство имеет счетную базу, сепарабельный упорядоченный континуум метризуем, сепарабельное регулярное пространство имеет не более чем континуальный вес и т. д..
Топологическое пространство — это пара 
, состоящая из множества 
и некоторого семейства 
подмножеств множества 
, удовлетворяющего следующим условиям:
(О1) 
и 
.
(О2) Если 
и 
, то 
.
(О3) Если 
, то 
.
Множество 
в этом случае называется пространством, его элементы называются точками пространства; подмножества 
, принадлежащие семейству 
, называются открытыми в пространстве 
; семейство 
открытых подмножеств пространства 
называется также топологией на . Пример 1.1. Пусть 
— множество, состоящее из двух элементов 
и 
. Множество 
можно задавать различные топологии:
а) 
, б) 
, в) 
, г) 
. Можно легко проверить, что 
есть топологические пространства.
Пример 1.2. Топология Зарисского. Рассмотрим произвольное бесконечное множество 
и семейство 
, состоящее из пустого подмножества 
и всевозможных подмножеств 
из , дополнения которых 
являются конечными подмножествами. Можно легко проверить, что семейство задает в топологию. Эта топология называется топологией Зарисского.
Американским математиком В.Комфортом был построен пример не сепарабельного пространства 
, Стоун-Чеховское расширение которого сепарабельно. В связи с этим возник вопрос: Для каких вполне регулярных пространств всегда существует сепарабельное бикомпактное расширение? В работах этот вопрос был решен. А именно, верна Теорема. Для вполне регулярного пространства 
следующие условия эквивалентны:
-
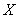слабо сепарабельно;
-
расширение Стоуна -Чеха
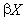пространства 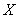сепарабельно;
-
всякая бикомпактификация
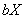пространства 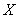сепарабельна;
-
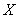имеет сепарабельное бикомпактное расширение.
Понятие слабо сепарабельного пространства введено В. И. Пономаревым.В работе изучается слабая плотность слабо аддитивных функционалов. Пусть 
— компакт, через 
обозначим множество всех непрерывных функций 
с обычными алгебраическими операциями и 
-нормой. Для каждого 
через 
обозначим постоянную функцию, определяемую по формуле 
для всех 
. Пусть 
. Будем говорить, что 
тогда и только тогда, когда 
для всех 
. Функционал 
называется:
1) слабо аддитивным, если
для любых 
и 
;
2) сохраняющим порядок, если для любой пары функций 
неравенство 
влечет 
;
3) нормированным, если 
. Для компакта 
через 
обозначается множество всех слабо аддитивных, сохраняющих порядок, нормированных функционалов 
[1].
Обозначим через 
(соответственно, через 
и 
) пространства всех слабо аддитивных функционалов с компактными носителями (соответственно, радоновых слабо аддитивных и 
-гладких слабо аддитивных функционалов) [3]
Теорема. Пусть 
— тихоновское пространство. Тогда
Следствие. Пусть — тихоновское слабо сепарабельное (сепарабельное) пространство, тогда пространства , , , 
тоже слабо сепарабельно (сепарабельно).
Литература:
- Radul T. N. On the funtor of order-preserving functionals.//Comment.Math.Unif.Carol. 1998.V,39.No.3.P.609–615.
-
Жиемуратов Р. Е. Топологические и категорные свойства пространства нелинейных
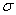-гладких функционалов. Канд. Дисс. Ташкент, ИМИТ, 2010, стр.69.
- Бешимов Р. Б. О слабой плотности топологических пространств // ДАН РУз. — 2000.– № 11. — С. 10–13.
