Рассмотрена задача нахождения определенного интеграла заданной функции на основе ее приближения двухточечными интерполяционными многочленами Эрмита. Получены конечные формулы для квадратур, использующие значения функции и ее производных до m-го порядка включительно, заданных в концевых точках отрезка интегрирования. Приведен пример вычисления определенного интеграла функции f(x)= sinxдля различных порядков производных, используемых при численном интегрировании.
Ключевые слова: квадратура функций, определенный интеграл, двухточечный многочлен Эрмита, квадратурные формулы с использованием производных.
Известными методами вычисления определенных интегралов — квадратуры функций -являются методы трапеций, Симпсона, Гаусса, Чебышева и другие, изложенные в [1–3].
Одним из подходов к нахождению определенных интегралов от заданной функции является подход, связанный с заменой данной функции, другой, более простой и к последующему вычислению интеграла от этой упрощенной функции. За приближенное значение интеграла от заданной функции принимается значение интеграла от приближающей функции.
Одним из направлений приближения функций является использования интерполяционных многочленов Эрмита, в котором используется данные о значениях не только функции, но и о ее производных до определенного порядка, заданных в узловых точках. Приближение функций с использованием частного вида многочленов Эрмита, именно двухточечных многочленов, когда значения функции и ее производных заданы только в двух концевых точках отрезка, рассмотрено в [4].
Целью данной работы является построение квадратурных формул, основанных на использовании двухточечных многочленов Эрмита.
1. Постановка ирешение задачи
Пусть функция f(x) определена на отрезке [x0,x1] и имеет достаточный набор производных на этом отрезке. Пусть также в обеих концевых точках отрезка [x0,x1] заданы значения функции f(x) и ее производных до порядка αi-1 включительно:
![]() (1.1)
(1.1)
Из условия существования производных следует, что для функции f(x) существует определенный интеграл
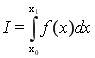 . (1.2)
. (1.2)
Необходимо приблизить этот интеграл интегралом, построенным по функции, которая является приближением к заданной функции f(x). В качестве приближающей функции будем использовать двухточечный многочлен Эрмита, рассмотренный в работе [7].
Согласно результатам работы [4, с. 1097] такой приближающий многочлен Hm(x), удовлетворяющий условиям (1.1) можно представить в различных формах, в частности, как:
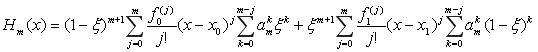 . (1.3)
. (1.3)
В формуле (1.3) для многочлена Hm(x) буквой ξ обозначена относительная переменная, связанная с исходной переменной x соотношением
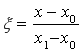 , (1.4)
, (1.4)
используется условие, что α0=α1=α, и буквой m обозначены порядки наивысших производных, используемых для построения двухточечного многочлена Hm(x), т. е. α — 1= m, откуда α = m +1, (1.5)
а коэффициент ![]() определен соотношением
определен соотношением
![]() . (1.6)
. (1.6)
В соответствие с формулой (1.6) коэффициент ![]() выражается через биноминальный коэффициент
выражается через биноминальный коэффициент ![]() (например, [5, с. 163])
(например, [5, с. 163])
![]()
согласно соотношению:
![]() (1.7)
(1.7)
Обозначим через L длину отрезка [x0,x1], определенную соотношением
L=x1-x0. (1.8)
Тогда формулу (1.3) с учетом формулы (1.4) и (1.8) для двухточечного многочлена можно переписать с использованием только относительной переменной ξ в виде:
![]() (1.9)
(1.9)
Для двухточечного многочлена Hm(x) можно построить определенный интеграл Im по отрезку [x0,x1], определенный соотношением
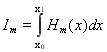 , (1.10)
, (1.10)
или, переходя к относительной переменной ξ, и используя (1.4) и (1.8), в виде:
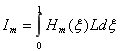 . (1.11)
. (1.11)
Подставляя (1.9) в (1.11) для определенного интеграла Im получим соотношение:
![]() . (1.12)
. (1.12)
Формулу (1.12) можно переписать в виде:
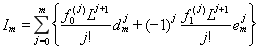 , где (1.13)
, где (1.13)
коэффициенты ![]() и
и ![]() определяются формулами
определяются формулами
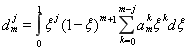 и (1.14)
и (1.14)
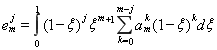 . (1.15)
. (1.15)
Сделав замену переменной в формуле (1.15) вида ![]() , учтя, что при этой замене имеет место равенство -dξ=dξ1 и изменятся пределы интегрирования, получим:
, учтя, что при этой замене имеет место равенство -dξ=dξ1 и изменятся пределы интегрирования, получим:
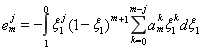 .
.
Поменяв местами пределы интегрирования, эту формулу в силу свойств интеграла можно записать в виде:
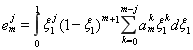 (1.16)
(1.16)
Из равенства правых частей формул (1.14) и (1.16) следует равенство левых частей, т. е.
![]() ,
,
поэтому в формуле (1.13) достаточно найти выражение, например, для коэффициента ![]() .
.
Формулу (1.14) для коэффициента ![]() , пользуясь свойством интеграла и степеней с одинаковыми основаниями, можно записать в виде:
, пользуясь свойством интеграла и степеней с одинаковыми основаниями, можно записать в виде:
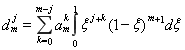 (1.17)
(1.17)
Интеграл вида 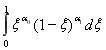 с использованием формул, представленных в [7, с. 743], можно записать в виде
с использованием формул, представленных в [7, с. 743], можно записать в виде
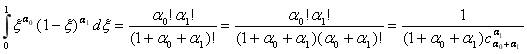 . (1.18)
. (1.18)
Из формулы (1.17) с использованием формул (1.18) и (1.7) для коэффициента ![]() получим соотношение:
получим соотношение:
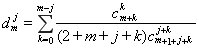 .(1.19)
.(1.19)
Проведя суммирование в правой части формулы (1.19) получим компактное выражение для коэффициента ![]() :
:
![]() . (1.20)
. (1.20)
Введя коэффициент ![]() , связанный с коэффициентом
, связанный с коэффициентом ![]() соотношением:
соотношением:
![]() , (1.21)
, (1.21)
для его значения получим формулу:
![]() . (1.22)
. (1.22)
В таблице 1 представлены коэффициенты ![]() для начальных значений m и j.
для начальных значений m и j.
Таблица 1
Коэффициенты ![]()
|
j m |
0 |
1 |
2 |
3 |
4 |
|
0 |
|
| |||
|
1 |
|
| |||
|
2 |
|
|
| ||
|
3 |
|
|
|
| |
|
4 |
|
|
|
|
|
Формулу (1.13) для представления интеграла Im можно записать в виде:
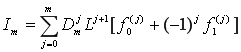 . (1.23)
. (1.23)
С использованием формулы (1.23) и коэффициентов, приведенных в таблице 1, получаются формулы для интеграла Im, которые представлены в таблице 2.
Таблица 2
Формулы численного интегрирования
|
s |
m |
Формулы для интеграла Im |
|
1 |
0 |
|
|
3 |
1 |
|
|
5 |
2 |
|
|
7 |
3 |
|
|
9 |
4 |
|
В первом столбце приводится значения s — степени двухточечного многочлена, определенной в соответствии с (1.9) соотношением:
s=2m+1.
Во втором столбце приведены значения m — максимального порядка производной, используемой для построения двухточечного многочлена.
Из формул, представленных в таблице 2, видно, что интеграл Im, выражается через значения функции и ее производных до m-го порядка включительно, заданных на концах отрезка интегрирования. Отметим, что коэффициенты перед производными зависят от m и j.
Случай m=0 соответствует известному методу трапеций [3, с. 6]. В этом случае двухточечный многочлен H0(ξ) имеет вид:
![]() , а интеграл I0 вычисляется как:
, а интеграл I0 вычисляется как:
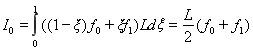 ,
,
что соответствует формуле для интеграла, представленной в [1, с. 106].
2. Пример численного интегрирования заданной функции
В качестве примера применения полученных квадратурных формул и оценки их погрешности вычислим значение интеграла от функции y= sinx на отрезке [0,π], т. е.
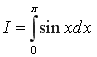 . (2.1)
. (2.1)
Находя первообразную функции y= sinx и используя формулу Ньютона-Лейбница [6, с. 408], определяем точное значение этого интеграла:
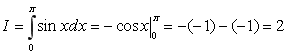 .
.
Используя квадратурные формулы, представленные в табл. 2, и значения производных подынтегральной функции, определяемые соотношением (см. [6, с.149]):
![]() , (2.2)
, (2.2)
вычислим значения интегралов Im, которые можно рассматривать как последовательные приближения к заданному интегралу I, определенному формулой (2.1).
Полученные значения Im для параметра m=0–4 представлены в третьем столбце таблицы 3. В четвертом столбце приведена погрешность приближения δIm, как модуль разности между точным и приближенными значениями интегралов, определенная по формуле
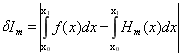 .
.
Таблица 3
Значения интеграла Im иего погрешности δIm
|
m |
Im |
δIm |
|
0 |
0.000000000 |
2.000000000 |
|
1 |
1.644934067 |
0.355065933 |
|
2 |
1.973920880 |
0.026079120 |
|
3 |
1.998952025 |
0.001047975 |
|
4 |
1.999973416 |
0.000026584 |
Из таблицы 3 видно, что по мере увеличения порядка используемых производных m, которые определяют порядок метода, значения интегралов Im стремятся к точному значению интегралаI, соответственно, погрешность δIm также стремится к нулю.
Можно показать, что для определенных классов функций, в частности, для функции y= sinx последовательность интегралов Im сходится к интегралу I, т.е ![]() .
.
Сходимость интегралов для рассмотренной функции y= sinx обусловлена ограниченностью производных этой функции на отрезке интегрирования.
Литература:
- Волков Е. А. Численные методы: Учебное пособие для вузов. — 2-е изд., испр. — М.: Наука. Гл. ред. физ.-мат. лит., 1987. — 248 с.
- Крылов В. И. Приближенное вычисление интегралов. — 2-е изд. — М.: Наука. Гл. ред. физ.-мат. лит., 1967. — 500 с.
- Никольский С. М. Квадратурные формулы. — 4-е изд. — М.: Наука. Гл. ред. физ.-мат. лит., 1988. — 256 с.
- Шустов В. В. О приближении функций двухточечными интерполяционными многочленами Эрмита // ЖВММФ, 2015, № 7, С. 1091–1108.
- Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся втузов. СПб.: Изд. Лань, 2010–608 с.
- Кудрявцев Л. Д.. Математический анализ. т. 1. М.: Высшая школа, 1970. — 592 с.
- Корн Г. Справочник по математике для научных работников и инженеров. — М.: Наука. Гл. ред. физ.-мат. лит., 1984–832 с.

