Рассмотрена задача построения многочлена, приближающего заданную функцию с известными значениями ее самой и определенного набора ее производных на концах заданного отрезка. Получены явные формулы представления аппроксимирующего многочлена в различных формах. Приведен пример представления функции y= cos x последовательностью двухточечных многочленов Эрмита, построенных для заданного отрезка. Проведено сравнение погрешностей приближения функции с использованием двухточечного представления и ее разложения в ряд Тейлора.
Ключевые слова: интерполяция Эрмита, многочлен Тейлора,формулы двухточечного представления, погрешность приближения функции на отрезке.
Введение. Функция, имеющая достаточное количество производных на некотором промежутке, с определенной степенью точности может быть приближена степенным многочленом. Так, если заданы значения производных в какой либо точке x0 этого промежутка, то функция f(x) может быть представлена [1, с. 549] в виде многочлена Тейлора с коэффициентами при степенях переменной, зависящими от значений производных в этой точке.
Однако точность приближения функции, многочленом Тейлора является, как правило, удовлетворительной лишь в окрестности точки разложения. Так, например, для функции y= cos x, как видно их графиков, представленных на рис. 1, погрешность аппроксимации неравномерна на отрезке разложения: если в окрестности точки разложения многочлен Тейлора хорошо приближает функцию, то при достаточном удалении от точки наблюдается существенное расхождение между многочленом и функцией. Наличие существенной неравномерности аппроксимации функции f(x) многочленом Тейлора отмечено также в работе [6, c. 30].
Одним из способов уменьшения погрешности и, соответственно, улучшения аппроксимации функции многочленом, является использование данных о значениях функции и ее производных не только в одной точке x0, но и в другой точке отрезка [x0,x1].
Многочлен, построенный по значениям функции и ее производных, заданных только в двух крайних точках отрезка, назовем двухточечным многочленом, а представление функции двухточечным многочленом можно назвать двухточечным представлением.
В работе рассматриваются вопросы представления многочлена, приближающего функцию, о которой известны ее значения и значения ее производных в концах заданного отрезка [x0,x1]. Кроме этого, исследуются вопросы, связанные с приближением функции последовательностью двухточечных многочленов.
Представление двухточечного многочлена в явном виде. Пусть в обеих концевых точках отрезка [x0,x1] заданы значения функции f(x) и ее производных до порядка mi включительно:
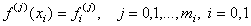 (1.1)
(1.1)
Необходимо построить многочлен, который удовлетворял бы условиям (1.1).
При построении этого многочлена воспользуемся решением задачи, называемой задачей Эрмита, для общего случая, в котором предполагается, что значения функции и ее производных известны в n+1 точке отрезка [x0,xn].
Формула для представления многочлена H(x), удовлетворяющего условиям (1.1), согласно, например, [2, с.172] в случае n=1, т.е. для отрезка [x0,x1], в наших обозначениях имеет вид:
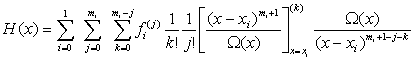 , (1.2)
, (1.2)
где Ω(x) определяется выражением:
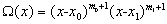 . (1.3)
. (1.3)
Формула (1.2) для случая двухточечного представления может быть существенно упрощена и представлена в удобном для дальнейшего использования виде.
После подъема членов формулы с отрицательными степенями в числитель дроби и выноса членов, не зависящих от индекса суммирования по k во внешние циклы, формула для многочлена H(x) примет вид:
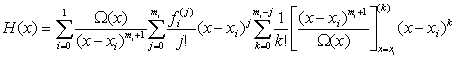 .
.
Введя обозначение
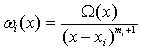 , (1.4)
, (1.4)
формулу для H(x) можно записать в виде:
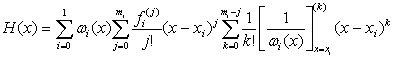 . (1.5)
. (1.5)
Выражение для ωi(x) в соответствии с (1.3) и (1.4) можно записать как:
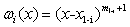 . (1.6)
. (1.6)
Последовательным дифференцированием и подстановкой при x=xi находим, что
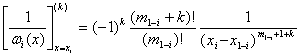 . (1.7)
. (1.7)
С учетом (1.7) формула (1.5) для H(x) получает вид:
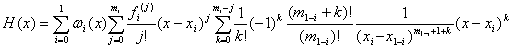 . (1.8)
. (1.8)
Выполнив дальнейшие несложные преобразования и учтя (1.6), получим, что:
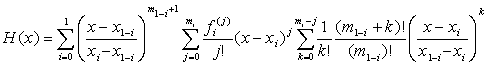 . (1.9)
. (1.9)
Обозначая дробное выражение под знаком внутренней суммы как 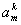 :
:
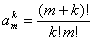 , (1.10)
, (1.10)
введя относительную переменную ξ, связанную с исходной переменной x соотношением
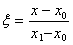 , (1.11)
, (1.11)
и записывая формулу (1.9) для многочлена H(x) без использования переменной суммирования i путем явной записи значений этой переменной, получим:
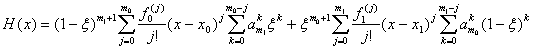 . (1.12)
. (1.12)
Заметим, что введенный коэффициент 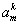 выражается через биноминальный коэффициент
выражается через биноминальный коэффициент 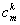 , определяемый соотношением
, определяемый соотношением
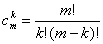 , (1.13)
, (1.13)
в виде:
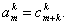 (1.14)
(1.14)
Ниже представлена часть таблицы коэффициентов 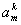 , полученная из соотношений (1.13) и (1.14).
, полученная из соотношений (1.13) и (1.14).
Таблица 1
Коэффициенты 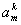 двухточечного представления
двухточечного представления
|
k m |
0 |
1 |
2 |
3 |
4 |
|
0 |
1 |
1 |
1 |
1 |
1 |
|
1 |
1 |
2 |
3 |
4 |
5 |
|
2 |
1 |
3 |
6 |
10 |
15 |
|
3 |
1 |
4 |
10 |
20 |
35 |
|
4 |
1 |
5 |
15 |
35 |
70 |
В случае, когда в крайних точках отрезка [x0,x1] порядок наивысшей производной один и тот же, т. е. при выполнении условия
m0= m1=m(1.15)
и при обозначении в этом случае многочлена H(x) как Hm(x), формула (1.12) для многочлена Hm(x) примет вид:
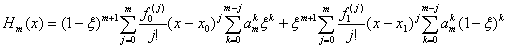 . (1.16)
. (1.16)
Если ввести длину L отрезка [x0,x1], определенную соотношением
L=x1-x0,
то формулу (1.16) для многочлена Hm(x) можно записать как:
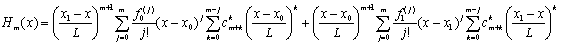 . (1.17)
. (1.17)
В данный формуле в отличие от предыдущей формулы (1.16) используется биноминальный коэффициент 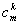 , связанный с коэффициентом
, связанный с коэффициентом 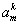 соотношением (1.14).
соотношением (1.14).
В частном случае, когда x0=0, т. е. для отрезка [0,L], представление двухточечного многочлена принимает вид:
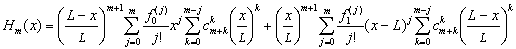 . (1.18)
. (1.18)
Пример использования двухточечного многочлена. Вкачестве примера использования двухточечного многочлена для аппроксимации функций найдем представление функции y= cos x на отрезке [0,L] с использованием этого многочлена.
Известно, что j-я производная функции y= cos x согласно, например, [1, с.179] представляется формулой:

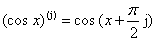 .
.
В соответствии с этим формулу (1.18) для приближающего ее многочлена Hm(x) можно записать в виде:
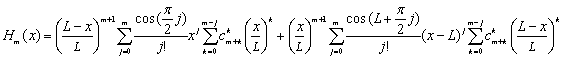 . (1.19)
. (1.19)
Выбирая различные значения длины отрезка разложения L, можно получить различные формулы для представления этой функции.
C использованием формулы (1.19) получены формулы приближения функции y= cos x на отрезке [0,π], которые представлены в таблице 2. Эти данные представлены в строках, соответствующих нечетным значениям переменной s, обозначающей степень многочлена приближения.
В строках таблицы, соответствующих четным значениям степени s многочлена разложения, для сопоставления приведены выражения, полученные по формуле Тейлора для этой функции
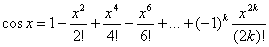 +…, k=0,1,2,… (1.20)
+…, k=0,1,2,… (1.20)
с соответствующим числом k членов разложения.
В каждой строке четвертого столбца, содержащего формулы разложения, сначала записывается точное символьное выражение и под ними приближенное с точностью до 10 знаков выражение с числовыми коэффициентами. Во втором и третьем столбце приводятся значения переменных k и m, определенных ранее соответствующими формулами (1.20) и (1.15), соответственно. В пятом столбце указано значение параметра числа точек n, в которых заданы значения функции и ее производных (n=0 для разложения по формуле Тейлора и n=1 для двухточечного разложения).
Из таблицы 2 видно, что выражения для разложения по формуле Тейлора содержит только члены с четными степенями переменной x, а формулы двухточечного разложения, наоборот, содержат только нечетные степени переменной x. Таким образом, в таблице 2 строки, соответствующие двухточечному представлению и разложению в ряд Тейлора чередуются между собой.
Таблица 2
Формулы двухточечного представления и разложения Тейлора для функции y= cosx
|
s |
k |
m |
Формулы в символьном и числовом представлении |
n |
|
0 |
0 |
1 1 |
0 | |
|
1 |
0 |
1–0.6366197724x |
1 | |
|
2 |
1 |
1–0.5000000000x2 |
0 | |
|
3 |
1 |
1–0.6079271019x2+0.129006138x3 |
1 | |
|
4 |
2 |
1–0.5000000000x2+0.04166666667x4 |
0 | |
|
5 |
2 |
1–0.5000000000x2–0.00841091630x3+0.0546765085x4–0.0069616293x5 |
1 | |
|
6 |
3 |
1–0.5000000000x2+0.0416666667x4–0.0013888889x6 |
0 | |
|
7 |
3 |
|
1 |
На рис. 1 и рис. 2 представлены графики разложений функции y= cos x, построенные по формулам, представленным в таблице 2 для разложений Тейлора и двухточечного представления. Из графиков наглядно видно, что для двухточечного представления при учете уже первой производной (m=1) аппроксимирующая зависимость визуально мало отличается от аппроксимируемой функции. Графики, построенные с использованием формул разложения Тейлора, имеют существенно большее расхождение с графиком исходной функцией, причем расхождение наиболее заметно в правой части отрезка разложения, наиболее удаленной от точки разложения x0=0.
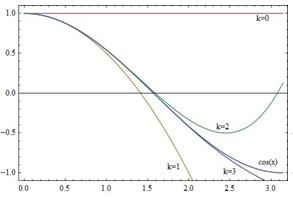
Рис. 1. Разложение по формуле Тейлора
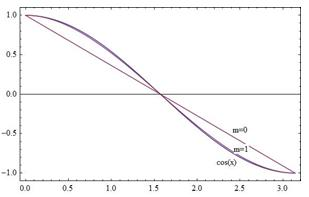
Рис. 2. Разложение по двухточечной формуле
Ниже, на рис. 3 и рис. 4 представлены графики погрешностей аппроксимации как модули разностей функции и ее приближения для функции y= cos x в случае разложения Тейлора и для двухточечного представления, соответственно. Из графиков, представленных на рис. 4, можно определить какое число членов разложения необходимо взять для достижения заданной точности. Так для достижения точности, лучшей чем 10-4, достаточно взять значение m=3 и использовать формулы, размешенные в последней строке таблицы 2 в символьном или числовом представлении.
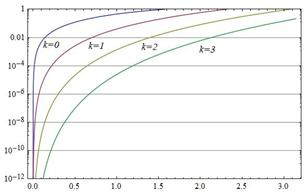
Рис. 3. Погрешность по формуле Тейлора
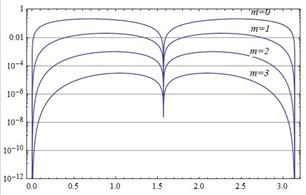
Рис. 4. Погрешность по двухточечной формуле
Заключение. Получены формулы представления функции, определенной на отрезке вместе с набором ее производных, в виде многочлена, коэффициенты которого определяются по значениям функции и ее производных, заданных в двух концевых точках этого отрезка.
Приведен пример представления y= cos x на заданном отрезке последовательностью двухточечных многочленов и дано сопоставление результатов двухточечного представления и разложения этой функции в ряд Тейлора.
Показано, что погрешность двухточечного представления по сравнению с разложением Тейлора при сопоставимых степенях приближающего многочлена является существенно меньшей, погрешность более равномерно распределена по заданному отрезку и обращается в нуль в обоих концах отрезка разложения.
Литература:
1. Кудрявцев Л. Д. Математический анализ. т. 1. М.: Высшая школа, 1970. — 592с.
2. Березин И. С., Жидков Н. П. Методы вычислений. Т. 1 — М.: Физматлит, 1962.– 464 с.
3. Кожухов И. Б., Прокофьев А. А.. Справочник по математике.- М.: «Лист», 1999.–640 с.
4. Гончаров В. И. Теория интерполирования и приближения функций. М.: Гостехтеориздат, 1934.–316 с.
5. Прасолов В. В. Многочлены. — М.: МЦНМО, 1999.– 336 с.
6. Волков Е. А. Численные методы: Учебное пособие для вузов. — 2-е изд., испр. — М.:Наука. Гл. ред. физ.-мат. лит., 1987. — 248 с.
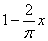
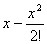
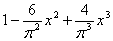
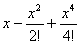
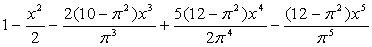
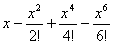
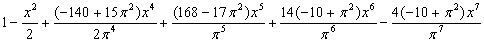 1–0.5000000000x2+0.0412901195x4+0.0007082067 x5–0.0018988547x6+0.0001726926x7
1–0.5000000000x2+0.0412901195x4+0.0007082067 x5–0.0018988547x6+0.0001726926x7
