При решении методом конечных элементов (МКЭ) задач изгиба плит на упругом оснований встречаются трудности, связанные с тем, что в рамках традиционной процедуры МКЭ можно рассматривать лишь ограниченные области, а применяемые математические модели оснований имеют бесконечное протяжение.
В данной статье излагается способ, позволяющий свести решение указанной задачи к выполнению стандартной схемы МКЭ для ограниченной области основания как «эквивалентный элемент».
В качестве модели основания была выбрана двухпараметрическая модель [1]. Предлагаемый подход предполагает выделение в общей расчётной схеме двух подобластей. Область плиты и часть зоны основания, дополняющая эту область до круговой, составляют внутреннюю подобласть Ω1, внешняя к ней неограниченная подобласть основания — Ω2.
Функционал полной потенциальной энергии системы из двух подобластей записывается в виде:
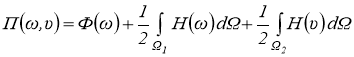(1)
При условии, что перемещения, описываемые функцией ω во внутренней круговой подобласти Ω1 и функцией 
— во внешней неограниченной подобласти Ω2, непрерывны при переходе границы раздела областей. В выражении (1) Ф(ω) обозначает функционал Лагранжа для плиты.
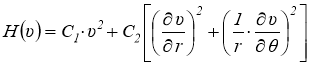(2)
Потенциальная энергия деформации параметрического основания (внутри подобласти Ω1) в полярных координатах, записывается в виде [2]:
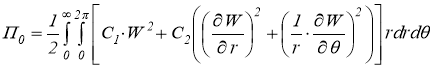,(3)
где W — прогибы точек поверхности основания; С1 — жёсткость модели основания на сжатие; С2 — жtсткость модели основания на сдвиг.
Вариационная задача об изгибе плиты на двухпараметрическом основании формулируется как задача определения функций ω и , доставляющих стационарное значение функционалу П(ω,υ) при дополнительном условии неразрывности на круговой границе r (рис. 1):
(4)
При приближённом решении поставленной вариационной задачи внутри круга (в области Ω1) для функции ω задаётся количественная аппроксимация:
(5)
где N — функция формы; q — вектор узловых перемещений. Аппроксимация функции υ в области Ω2 осуществляется в аналогичной (4) форме:
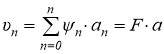(6)
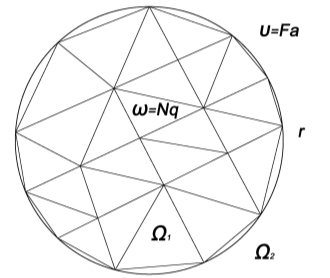
Рис. 1. Схема разделения расчётной области на подобласти Ω1, Ω2
Но здесь функции Ψn выбираются такими, чтобы они заранее удовлетворяли разрешающему одному уравнению в области Ω2 и условиям отсутствия перемещений на бесконечности. Для двухпараметрической модели таким уравнением является следующее:
.
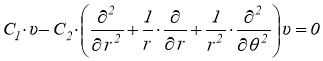Опираясь на аналитическое решение этого уравнения [2]; систему функций {Ψn}можно принять в виде:
,
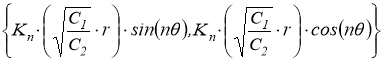где Kn — функция Макдональда с целочисленным индексом. Данная система функции является полной, линейно-независимой, а при фиксированном r — ортогональной на промежутке [0, 2π].
Из (3) и (5) следует общее выражение для матрицы жесткости элемента основания:
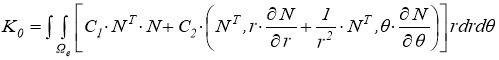(7)
Внешняя расчётная область представляет собой неограниченную мембрану с круговым отверстием на винклеровском основании. Эта зона рассматривается как элемент основания бесконечной протяжённости с узлами по круговой границе. Ниже описываются посторонние матрицы жёсткости этого элемента.
Узлы внутренней и внешней областей считаются общими (рис. 2). Перемещения точек рассматриваемого элемента основания определяются как решение одного уравнения (8) [3]:
Реакция основания для данной модели внутри подобласти Ω1:
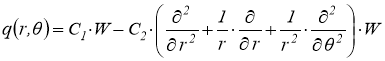(8)
Прогибы точек выпираемой части основания:
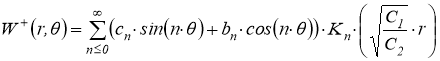(9)
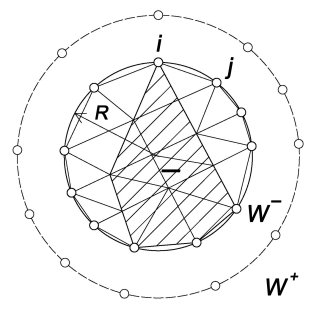
Рис. 2.
Число членов n разложений ограничивается в соответствии с количеством условий неразрывности перемещений в узлах на границе областей, которые необходимо выполнить. В данной работе для расчёта плит используются несовместные конечные элементы в виде произвольного треугольника кольцевого сектора. Узловыми параметрами элементов являются прогибы и углы поворота. В первом случае –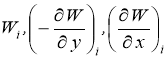
, во втором — 
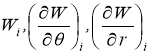. Совместность прогибов вдоль круговой границы обеспечивается при удовлетворении следующих условий неразрывности в узлах:
,
.
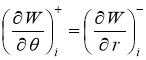Следовательно, если число членов в ряде (9) берётся равным удвоенному числу граничных узлов, то неизвестные коэффициенты разложения могут быть выражены через указанные компоненты вектора перемещений граничных узлов:
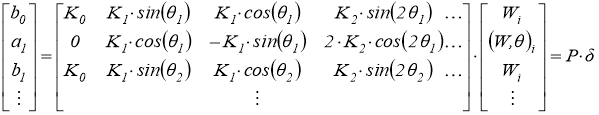(10)
На основании (9) и (10) матрица интерполирующих функций для элемента основания бесконечной протяжённости с узловыми параметрами δ имеет вид:
(11)
Обращение матрицы P проводится численно.
В результате выполнения матричных операций и интегрирования по θ матрица жёсткости элемента основания может быть записана следующим образом:
(12)
В силу ортогональности системы {sin(nθ), cos(nθ)}, где n — целое на промежутке [0, 2π], матрица А — диагональная:
её общий член:
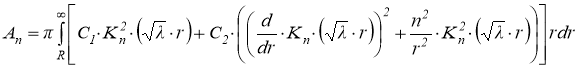
где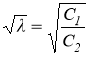 
. С использованием следующих рекуррентных соотношений для бесселевых функций [5]:
,
,
,
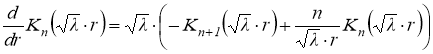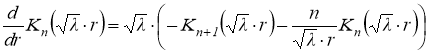преобразуется второй подынтегральный член:
.
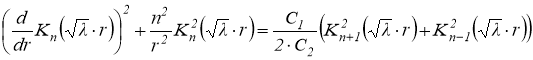Интегралы от произведений бесселевых функций вычисляются по формуле [5]:
.
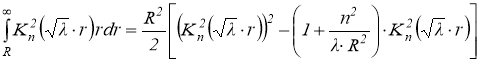Окончательное выражение для общего члена матрицы A:
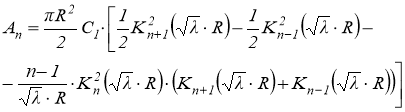(13)
При расчёте плит в виде кольца матрица жёсткости элемента внутреннего круга основания может быть построена аналогично (12) и (13), если вместо функций Knиспользовать модифицированные функции Бесселя первого рода In и брать компоненты матрицы A с обратным знаком.
Если проводится расчёт плиты на основании Винклера, т. е. коэффициент С2 = 0, то элементы матрицы жёсткости основания бесконечной протяжённости являются нулевыми вследствие Kn(r)= 0. Это отвечает механической стороне модели основания Винклера, не работающего за пределами площади опирания.
Как было указано выше, в качестве узловых параметров построенного элемента основания рассматривается прогиб Wt и угол поворота вокруг оси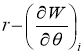 
. При расчёте систем в декартовых координатах необходимо провести переход к неизвестным
.
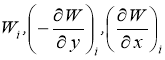Используя соотношение:
.
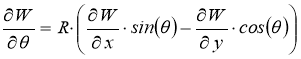Блоки матрицы жёсткости основания пересчитываются следующим образом:
,
где: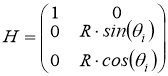 
.
С использованием построенного элемента основания бесконечной протяжённости была решена следующая задача: круглая плита на основании с двумя упругими характеристиками, загруженная по внешнему контору равномерно распределённой нагрузкой (рис.3). Схемы разбивки области на секторные и треугольные конечные элементы изображены на рис. 4 и 5. Результаты расчётов в табл. 1.
Таблица 1
|
Разбивка |
Прогиб центра пластины, мм |
|
|
элемент кольцевого сектора (рис. 4) |
треугольный элемент (рис. 5) |
|
|
а |
5,5300 |
5,9200 |
|
б |
5,5280 |
5,6802 |
|
в |
- |
5,6097 |
|
Точное решение |
5,5279 |
|
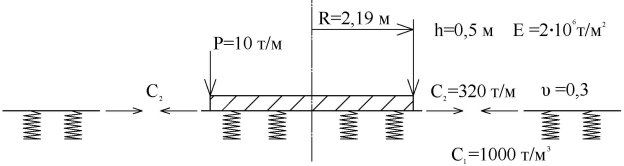
Рис. 3.
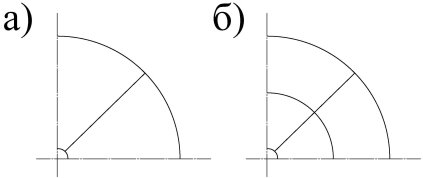
Рис. 4.
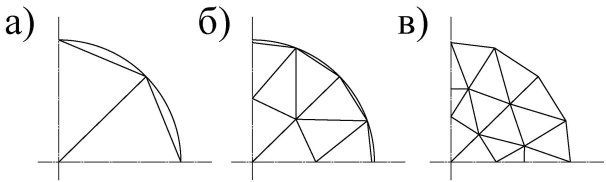
Рис. 5.
Литература:
- Филоненко-Бородич М. М. Некоторые приближенные теории упругого основания/ М. М. Филоненко-Бородич //Ученые записки. Москва: МГУ, 1940. Вып. 46. С. 46–54.
- Корнев Б. Г. Некоторые задачи теории упругости и теплопроводности, решаемые в бесселевых функциях. М.: Физматгиз, 1960. 458 с.
- Власов В. Э., Леонтьев Н. Н. Балки, плиты и оболочки на упругом основании.- М.: Физматгиз, 1960, с.491.
- Влоукова К. П., Сливкер В. И. Некоторое особенности МКЭ при расчёте конструкций на упругом основании. — В кн.: Метод конечных элементов и строительная механика. — Л.: Труды Ленингр. политехн. ин-та. 1976, № 349, с.69–80.
- Грей Э., Мэтьюз Г. Б. Функции Бесселя и их приложения к физике и механике. — М.: И. Л., 1953, с.371.
- Пастернак П. Л. Основы нового метода расчёта фундаментов на упругом основании при помощи двух коэффициентов постели. М.: Стройиздат, 1954, с.55.
- P. Ruge, C. Trinks, S. Witte Time-domain analysis of unbounded media using mixed-variable formulations. Earthquake engineering and structural dynamics. 2001. 30 Pp. 899–925.
- U. Basu, A. K. Chopra Perfectly matched layers for time-harmonic elastodynamics of unbounded domains: theory and finite-element implementation. Computer methods in applied mechanics and engineering. 2003. 192. Pp. 1337–1375.
