Статья посвящена одному из разделов начертательной геометрии — проецированию модели по ортогональным плоскостям 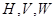 проекции. Показано построение на одной модели три и более геометрические фигуры.
проекции. Показано построение на одной модели три и более геометрические фигуры.
Ключевые слова: проекция, плоскость, построение, модель, призма, пирамида, цилиндр, конус, окружность, метод, горизонталь, фронталь, профиль, ось, координата.
В статье [1] приводится построение двух геометрических фигур на одной модели методом деления окружности радиусом 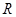 на равные их части и построение на них геометрических фигур многогранников в трех плоскостях
на равные их части и построение на них геометрических фигур многогранников в трех плоскостях 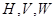 проекции. Нами решается та же задача, но с построением на одной модели трех и более геометрических фигур различных конфигураций. Для визуальной наглядности данного примера, мы показываем на моделях различные геометрические фигуры: призму, пирамиду, цилиндр, конус, а также их производные: усеченной (горизонтальной и наклонной) плоскостью призму, пирамиду, цилиндр и конус. Студенты на рабочих тетрадях по выданным вариантам самостоятельно выбирают эти фигуры в начале в одной горизонтальной
проекции. Нами решается та же задача, но с построением на одной модели трех и более геометрических фигур различных конфигураций. Для визуальной наглядности данного примера, мы показываем на моделях различные геометрические фигуры: призму, пирамиду, цилиндр, конус, а также их производные: усеченной (горизонтальной и наклонной) плоскостью призму, пирамиду, цилиндр и конус. Студенты на рабочих тетрадях по выданным вариантам самостоятельно выбирают эти фигуры в начале в одной горизонтальной 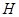 плоскости, затем проецируют их во — фронтальную проекцию и — профильную
плоскости, затем проецируют их во — фронтальную проекцию и — профильную 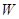 . В горизонтальной
. В горизонтальной 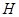 плоскости чертят несколько геометрических тел в виде модели, например, цилиндр, выглядит как окружность, далее вписывают в круг призму, пирамиду и конус. В дальнейшем построения их производят по фронтальным
плоскости чертят несколько геометрических тел в виде модели, например, цилиндр, выглядит как окружность, далее вписывают в круг призму, пирамиду и конус. В дальнейшем построения их производят по фронтальным 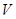 и профильным
и профильным 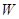 проекциям по запланированным последовательностям: призму, цилиндр и пирамиду или же — пирамиду, цилиндра и призму.
проекциям по запланированным последовательностям: призму, цилиндр и пирамиду или же — пирамиду, цилиндра и призму.
Выдаются студентам задания по соответствующим вариантам, например:
- построить на горизонтальной 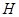 плоскости окружность диаметром Ø
плоскости окружность диаметром Ø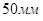 и разделить их на четыре равнодольные части;
и разделить их на четыре равнодольные части;
- начертить на данной окружности два четырехгранника вписанным и описанным в окружность;
- спроецировать из горизонтальной 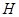 на фронтальную
на фронтальную 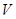 и профильную
и профильную 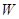 плоскости проекции модель состоящий из: призмы, цилиндра и пирамиду с высотой по
плоскости проекции модель состоящий из: призмы, цилиндра и пирамиду с высотой по 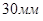 .
.
Строим на формате А4 три ортогональные проекции по координатным 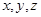 осям: горизонтальную
осям: горизонтальную 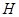 , фронтальную
, фронтальную 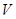 и профильную
и профильную 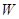 плоскость для модели геометрических тел эпюры Монжа. Построение геометрической модели начинаем с горизонтальной
плоскость для модели геометрических тел эпюры Монжа. Построение геометрической модели начинаем с горизонтальной 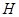 плоскости проекций (рисунок 1, а). В центре горизонтальной плоскости
плоскости проекций (рисунок 1, а). В центре горизонтальной плоскости 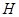 проводим вспомогательные осевые линии и на пересечении их обозначим буквой
проводим вспомогательные осевые линии и на пересечении их обозначим буквой 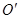 , которая является центром окружности круга диаметром Ø
, которая является центром окружности круга диаметром Ø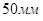 данной модели. На концах их при пересечении круга и осевых линиях фиксируем буквами
данной модели. На концах их при пересечении круга и осевых линиях фиксируем буквами 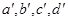 и соединяя эти точки контурными линиями получаем вписанный в окружность четырехгранник
и соединяя эти точки контурными линиями получаем вписанный в окружность четырехгранник 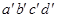 . До построения описанного в окружности четырехгранника
. До построения описанного в окружности четырехгранника 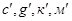 определяем высоту
определяем высоту 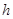 вершины по хорде
вершины по хорде 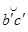 , которая является расстоянием между параллельными линиями
, которая является расстоянием между параллельными линиями 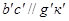 . Строим вспомогательную линию
. Строим вспомогательную линию 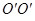 (рисунок 1, а) из точек
(рисунок 1, а) из точек 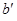 и
и 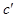 радиусом
радиусом 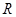 проводим две засечки и на их пересечении фиксируем точку
проводим две засечки и на их пересечении фиксируем точку 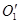 . Соединяем эти две точки
. Соединяем эти две точки 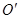 и
и 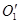 вспомогательной линией и фиксируем буквами
вспомогательной линией и фиксируем буквами 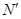 и
и 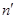 . Отрезок между ними является высотой
. Отрезок между ними является высотой 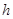 хорды
хорды 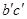 :
: 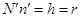 . Проводим относительно касательную линию
. Проводим относительно касательную линию 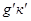 (рисунок 1, б) окружности, которая является параллельной линией
(рисунок 1, б) окружности, которая является параллельной линией 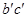 , т. е.
, т. е. 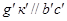 с расстоянием отрезка
с расстоянием отрезка 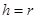 . На концах пересечении касательных и вертикально-горизонтальных осевых линиях фиксируем точки
. На концах пересечении касательных и вертикально-горизонтальных осевых линиях фиксируем точки 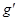 и
и 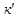 . Этим же методом получаем остальные три касательные линии описанной окружности и фиксируем точки
. Этим же методом получаем остальные три касательные линии описанной окружности и фиксируем точки 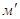 и
и 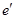 . По полученным фиксируемым точкам соединяем их контурными линиями и получаем четырехугольник
. По полученным фиксируемым точкам соединяем их контурными линиями и получаем четырехугольник 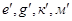 .
.
Рис. 1. Графический способ построения четырехгранников
Перед тем, как перейти к фронтальной  плоскости проекции, мы в горизонтальной
плоскости проекции, мы в горизонтальной  плоскости определяем три геометрические фигуры: пирамиду, цилиндра и призму. Вписанный в окружность четырехгранник
плоскости определяем три геометрические фигуры: пирамиду, цилиндра и призму. Вписанный в окружность четырехгранник 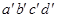 выбираем как проекцию пирамиды, для этого соединяем точки
выбираем как проекцию пирамиды, для этого соединяем точки 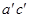 и
и 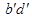 контурными линиями (рисунок 1, б) и на пересечении этих линий фиксируем точку
контурными линиями (рисунок 1, б) и на пересечении этих линий фиксируем точку 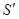 , которая является высотой вершины пирамиды. Контур окружности является цилиндром, а описанный по окружности контур четырехгранника
, которая является высотой вершины пирамиды. Контур окружности является цилиндром, а описанный по окружности контур четырехгранника 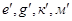 является призма. Из горизонтальной
является призма. Из горизонтальной 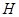 плоскости проекции (рисунок 2) проводим ортогональные линии все фиксируемые точки призмы
плоскости проекции (рисунок 2) проводим ортогональные линии все фиксируемые точки призмы 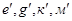 на фронтальную
на фронтальную 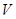 плоскость проекции. Фиксируем их на координатной оси
плоскость проекции. Фиксируем их на координатной оси 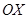 нижнюю часть призмы
нижнюю часть призмы 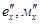 ,
, 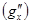 и
и 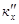 , а также на высоте координатной оси
, а также на высоте координатной оси 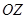
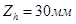 верхнюю часть призмы
верхнюю часть призмы 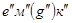 , при этом на данную высоту
, при этом на данную высоту 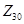 проецируем с горизонтальной
проецируем с горизонтальной 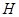 плоскости проекцию цилиндра и фиксируем их точками
плоскости проекцию цилиндра и фиксируем их точками 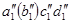 а на уровне
а на уровне 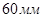 по оси
по оси 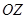 верхнюю часть цилиндра точками
верхнюю часть цилиндра точками 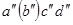 . Эти точки являются нижним основание призмы
. Эти точки являются нижним основание призмы 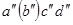 с вершиной
с вершиной 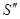 , которую выбираем по высоте оси
, которую выбираем по высоте оси 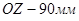 . Соединяя их контурными линиями получаем пирамиду.
. Соединяя их контурными линиями получаем пирамиду.
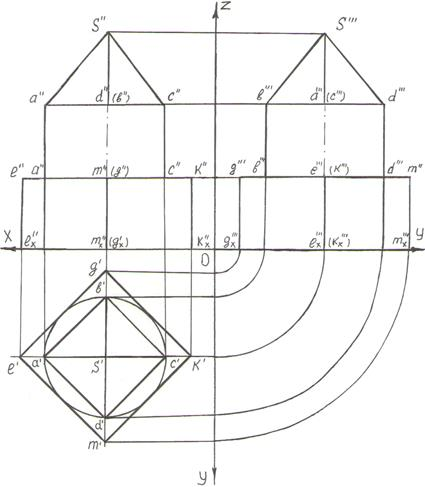
Рис. 2. Построение трех фигур на одной модели
Спроецировав все фиксируемые точки 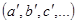 с горизонтальной
с горизонтальной 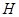 и фронтальной
и фронтальной 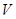 на третью профильную
на третью профильную 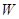 плоскость проекции по соответствующим точкам мы получим третий вид модели состоящей из трех геометрических фигур: призмы, цилиндра и пирамиды.
плоскость проекции по соответствующим точкам мы получим третий вид модели состоящей из трех геометрических фигур: призмы, цилиндра и пирамиды.
По вышеприведенной методике провели построение четырех геометрических фигур на одной модели на различных плоскостях  проекции (рисунок 3). На нижнем основании модели расположена призма (I) над ним, усеченная пирамида (II), далее расположили цилиндр (III) и на вершине модели конус (IV). Расположение геометрических фигур на модели можно спроектировать и в другом варианте: на нижнем основании модели можно установить усеченную пирамиду, над ним расположить призму, далее цилиндр и сверху конус. Перестановки фигур зависит от выбора студента.
проекции (рисунок 3). На нижнем основании модели расположена призма (I) над ним, усеченная пирамида (II), далее расположили цилиндр (III) и на вершине модели конус (IV). Расположение геометрических фигур на модели можно спроектировать и в другом варианте: на нижнем основании модели можно установить усеченную пирамиду, над ним расположить призму, далее цилиндр и сверху конус. Перестановки фигур зависит от выбора студента.
Рис. 3. Построение четырех фигур на одной модели
Из вышеприведенного можно сделать следующие выводы:
- при построении модели необходимо начать строить геометрические фигуры в горизонтальной  плоскости, в начале необходимо начертить окружность, разделив их на равные части (4, 5…) и построить вписанный, а затем уже описанный многогранник;
плоскости, в начале необходимо начертить окружность, разделив их на равные части (4, 5…) и построить вписанный, а затем уже описанный многогранник;
- определить на горизонтальной 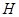 плоскости количество и расположение геометрических фигур — призму, цилиндра, пирамиду и конус, а затем спроектировать их на фронтальную
плоскости количество и расположение геометрических фигур — призму, цилиндра, пирамиду и конус, а затем спроектировать их на фронтальную 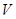 и профильную
и профильную 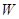 плоскости.
плоскости.
Литература:
1. Алимов Б. М., Пулатова Х. А. Метод построения двух геометрических фигур на одной модели. // Молодой ученый. — 2014. № 9 (68). — С. 98–101.







