В статье даны методические материалы по обеспечению преемственности и непрерывности процесса совершенствования графической грамотности учащихся путем использования законов перспективы, изложены методические рекомендации по использованию их на уроках изобразительного искусства через конкретные графические примеры.
Ключевые слова: изобразительное искусство, черчение, перспектива, пространство, форма, конструкция, светотень, внедрение, преемственность, эффективность, графическая грамотность
Methodical materials are given in article on provision of receivership and continuity of the process of the improvement to graphic literacy students by use the laws of the prospect, are stated methodical recommend on use them on lesson graphic arts through concrete graphic examples.
Keywords: graphic arts, drawing, prospect, space, the form, design introduction, receivership, efficiency, graphic literacy
В настоящее время созданы все условия и основные дидактические требования для повышения эффективности качества всех видов непрерывного образования. В качестве основных критериев и наиболее важных факторов для повышения качества, и эффективности обучения во всех сферах образования является интеграционный подход. Например, для обучения общественных наук возможно получение эффективных результатов при использовании законов перспективы, которая входит в число точных предметов. Мы используем различные методы для длительного сохранения в памяти образы окружающих нас предметов. Самым эффективным методом является перспективное изображение предметов на плоскости. Так как создание перспективного изображения предметов позволяет всестороннему анализу элементов предмета, а также сознательное понимание пространственной формы предмета. После такой практики у человека будет формироваться привычка к анализу каждого увиденного предмета, результатом которого происходит развитие способности длительного сохранения в памяти пространственных образов. В зависимости от точки зрения наблюдающего, размера и расстояния наблюдаемого предмета, идет разумное постижение изменения предметов в пространстве. В процессе построения перспективного изображения на двухмерной плоскости, в независимости от точки зрения, можно точно и правильно построить третий вид предмета.
Значит, самым эффективным средством, позволяющим, пространственное отображение предмета, это перспектива картины или чертёжа, полученная методом центрального проецирования.
Человеческий глаз видит окружающие кго предметы, в результате освещения каким-либо источником света.
Тень в перспективе играет основную композиционную роль в раскрытии содержания произведения. Если наблюдать окружающие предметы, то можно увидеть различие в их освещении.
Предметы, расположенные близко к источнику света, когда лучи падают на поверхность предмета под углом 90º, то эти поверхности будут освящены намного сильнее, а если наоборот, то степень освещения будет уменьшаться. А повехности, куда лучи света совсем, не попадают, будут темными.
Различное освящение предмета или рельефной поверхности, помогает образному представлению его пространственной формы. Художники свет и тень передают с помощью штриховки, тушёвки, тонирования, с так же силой света [1]. При создании образной композиции или изображении, какого — либо предмета, неоходимо знать правильное распределение света на поверхности предмета и законы построения предметов. Знания этих же законов необходимо так же и при рисовании с натуры.
Собственная и падающая тени предметов образуются следующим образом (рис.1). Лучи света, выходящие из точки S, которая, является источником света, освещают плоскость К. Если, на их пути, будет находиться какой-либо предмет, то лучи света загораживаются, и на плоскости появляется неосвещенная часть. Одна часть предмета будет освещена, а другая будет в тени. Такая часть предмета называется падающей тенью предмета. Освещенная часть предметата называется собственной тенью предмета. Линия, которая делит освещенную и неосвещенную части предмета называется контуром собственной тени или линией, которая делит свет и тень.

Рис. 1.
Построение падающей и собственной тени предмета связаны с условиями освещения. Существуют два вида освещения: искусственное и природное.
Тени, повышая целостность аксонометрической проекции, облегчают чтение и пространственное представление о предмете. Как и в ортогональных проекциях, так и в аксонометрических проекциях построение тени, осуществляется путем определения точки пересечения лучей света с плоскостью (или поверхностью) предмета (эта задача является основой для построения теней).
Построение падающей и собственной тени предмета связаны с условиями освещения. Существуют два вида освещения: искусственное и природное.
Тени, повышая целостность аксонометрической проекции, облегчают чтение и пространственное представление о предмете. Как и в ортогональных проекциях, так и в аксонометрических проекциях построение тени, осуществляется путем определения точки пересечения лучей света с плоскостью (или поверхностью) предмета (эта задача является основой для построения теней).
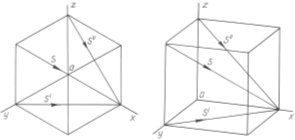
Рис.2.
Построение собственной и падающей теней геометрических тел. На рис. 3 показано построение в диметрической проекции падающих теней в координатную плоскость четырехсторонней призмы.
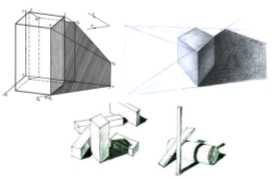
Рис. 3
Для построения тени переднего вертикального ребра АВ, проводим световую плоскость N. Световая плоскость пересекает горизонтальную плоскость проекции параллельно s', а фронтальную плоскость проекции пересекает по вертикальной линии. Световой луч проходящий из точки А параллельно s', пересекая вертикальную линию даёт точку As, то есть тень точки А на фронтальной плоскости. Ломаная линия BS1AS является тенью ребра AB. Таким же способом определив точки CS и DS, взаимно их, пересекая, получим контур тени, падающей с призмы. Правая и задняя стороны призмы будут погружены в собственной тени.
На рис.5 изображена в диметрии прямоугольная пирамида. Рассмотрим построение падающей тени от пирамиды на горизонтальную (H) и фронтальную (V) плоскости. Проводим прямые параллельные линии от вершины пирамиды T до s и основания пирамиды от T' до s'. Взаимно пересекаясь, эти линии образуют вспомогательную тень T1S на горизонтальной плоскости точки T.
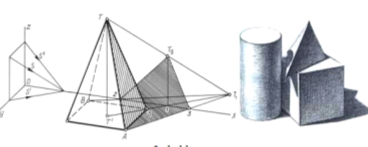
Рис. 4
Проводим вертикальную линию от точки 1, образованную от пересечения T'T1S и оси x, обозначим точку TS, полученную при пересечении его с T T1S. Ломаная линия T'1TS будет тенью T T' высоты пирамиды. От точки T1S в основе пирамиды проводим касательные T1SA и T1SB. Эти линии определяют контуры пирамиды в горизонтальной плоскости и грани TA' и TB, являющиеся границами собственной тени пирамиды. T1SA, являющаяся тенью рёбер TA и TB, а так же отрезки T1SB пересекают ось x в точках 2 и 3. Объединяя точки 2 и 3 с точкой TS, образуем тень пирамиды, на фронтальной плоскости. Стороны TAD и TDB пирамиды находятся в собственной тени.
На рис.6 показано построение тени на диметрической проекции прямого круглого цилиндра с основанием, лежащей на горизонтальной плоскости. Для начала определим контур собственной тени цилиндра. Для этого проведём параллельно касательные по направлению s' в основании пирамиды. Для точного определения точек касания, с центра основания цилиндра проведём паралелельную линию к OF, являющейся основной диагональю луча куба, эта линия, пересекая касательные, образует точки касания A и B.
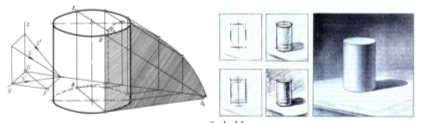
Рис. 5
Образующие AD и BE, проходящие через точки A и B, являются контурами собственной тени цилиндра. Построим тени этих образующих, на горизонтальной и фронтальной плоскостях (смотрите на рис. 3). Для построения тени верхнего основания цилиндра, необходимо наметитить не нём несколько произвольных точек и определить их тени. Взаимно сопрягая обозначенные точки, образуем контур падающей тени.
На рис. 6 показано построение теней округлого конуса. Подобно определению теней пирамиды, сначала определяются тени T1S на плоскости H и TS на плоскости V вершины конуса T. Проводим касательные через точку T1S в основании конуса, и образуем касательные точки А и В. Образующие ТА и ТВ, являются границами собственной тени конуса. Отрезки T1SA и T1SB пересекают ось x в точках 2 и 3. Сопрягая эти точки с точкой TS образуем тень, падающую на плоскость V.
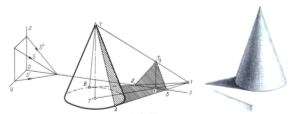
Рис. 6
Построение собственной и падающей тени сферы. Чтобы упростить понимание чтения чертежа, отдельно выполним построение собственной и падающей теней сферы. Будучи окружностью, горизонтальная проекция n', собственной тени сферы, его радиус равен отрезку ОА. Определение отрезка ОА видно на чертеже. Диаметр BD сферы, расположенный перпендекулярно к лучам света, является большой осью собственной тени n, которая имеет вид эллипса. Будущий эллипс, повернув вокруг диаметра BD, опустим на поверхность очерка сферы. Разделим на равные части очерк сферы и проекцию n' собственной тени и повернём назад точки на очерке (они будут двигаться по направлению луча).
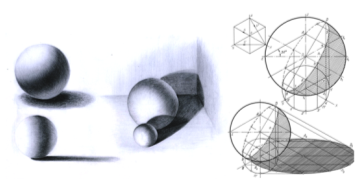
Рис. 7
Вертикальные линии, идущие из точек окружности n', пересекаясь с одноименными линиями движения на очерке, образует точки, относящиеся к контуру собственной тени. Плавно сопрягая эти точки, образуем эллипс, который является контуром собственной тени.
На рис.7 показано построение падающей тени сферы. Контур падающей тени сферы, будучи в форме эллипса, определён, взаимопересечением точек окружности n' и точек эллипса n.
Построение собственной и падающей теней сферы, путем создания гомологического согласования. Из вышеприведённых примеров нам стало ясно, что собственная и падающая тени сферы имеют форму эллипса. Для построения этих эллипсов, по-первых устанавливается соответствие между контуром собственной тени и аксонометрической проекцией сферы, во-вторых, устанавливается соответствие между контуром падающей тени и контуром собственной тени. В первом случае ось соответствия перпендекулярно оси аксонометрической плоскости и направлением луча и является линией пересечения плоскости луча проходящей через центр сферы. Во-втором случае, ось соответствия — это плоскость света, перепендекулярная горизонтальной плоскости, то есть является линией пересечения плоскости, на которой лежит контур собственной тени сферы.
Для определения направления и позиций осей соответствия, воспользуемся аксонометрической проекцией лучей куба.
Для определения направления лучей света и осей соответствия построим диметрию куба.
На рис.8 в диметрической проекции показано построение падающих теней от прямоугольной призмы и пирамиды. Для начала построим падающие тени от призмы и пирамиды на горизонтальную плоскость. Определим традиционным образом контур падающей тени, от точек в пространстве проведём параллели к лучу света, путем взаимопересечения параллельно проведённых лучей относительно горизонтальных проекций. Пропустив противоположно направленный луч, пределим тень, падающую от ребра призмы к передней оси пирамиды. Для этого от точки KS, полученной от пересечения контуров падающих теней, проведем противоположно направленный луч. Данный луч, пересекаясь с отбрасывающим тень ребром пирамиды, образует точку К. Падающая тень, проходя через точку К, будет параллельна к отбрасывающему тень ребру призмы.
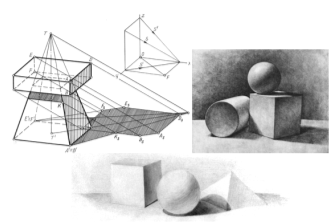
Рис. 8
На рис.10 мы видим тень, падающую от цилиндра на конус. Чертёж выполнен в изометрии. Основание конуса и диаметр цилиндра равны. Для построения падающей тени конуса, достаточно определить тень вершины TS.
Начертив касательные от точки TS к основанию конуса, мы получим образующие TB и TD, являющиеся контурами собственных теней конуса. Падающую тень цилиндра определим так же, как на рис.8. Для построения контура падающей от цилиндра к конусу тени, воспользуемся противоположно направленными лучами.
На рис. 9 точка F1S, на собственной тени определена, путем проведения противоположных лучей из точек ES и FS. Определим точку N1S, которая проходит через точку K и падает на образующую KT. KTS, является падающей на горизонтальную плоскость тенью образующей KT. Эта тень пересекается с падающей тенью цилиндра в точке NS. Если мы точку NS проецируем противоположно направленным лучом к образующей KT, то получим точку N1S.. Ломаная линия E1SN1SF1S является контуром тени, падающей на поверхность конуса.
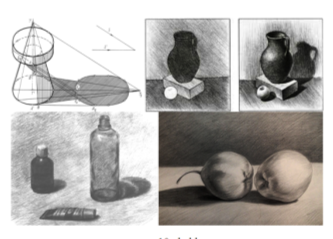
Рис. 9
Построение теней колонн и парадной лестницы зданий. Для получения отвечающей требованиям тени, обозначим положение солнца и начертим схему движения солнечных лучей. В этой задаче так же направление луча не соответствует направлению диагонали куба.
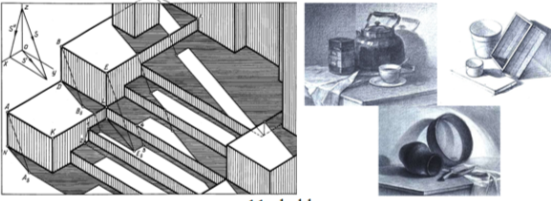
Рис. 10
Из чертежа ясно видно определение теней точек А и В, а так же проходящих через них теней ребёр (AN, AK, BD, BE). (Рис.10) Тени, падающие с ребер лестницы на ступеньки, определены путем проведения параллельных линий от точки 1 по направлению к S''. Для построения падающих от перегородки лестницы EF теней к ступенькам, с какой-либо точки на ней, например, точки E, определим тень ES. Если проведем параллель от точки ES к ребру EF, получим на ступеньке тень ребра ES3. Параллельно проводим от точки 3 к направлению s противоположно направленный луч, получим точку 4 на ребре лестницы. Из точки 4 тень ребра EF ляжет параллельно самой-себе. Точно таким же способом построим все тени ребер KL и EF на всех лесничных ступеньках. Тени, падающие от колонн и невидимых сторон здания, можно понять из чертежа.
Такие законы обучения изобразительному искусству невозможно без применения перспективного представления. Известно, что перспектива считается одним из основных законов изобразительного искусства.
В заключении хочется добавить, что объяснение законов перспективы на примере произведений художников, имеет обоюдно эффективный результат:
– Законы, точной науки обеспечивают изобразительную грамотность;
– Раскрывает глубину, пространство, третье измерение и идею произведений художников, выполненных в реалистической манере;
– Мастерски используя законы природы (дневной свет), художники будут наиболее точно изображать свет, тень и рефлексы на предметах [2];

Литература:
- М.Мaкaрова. “Перспектива”. Просвещение. Москва, 1989
- А.Абдурахманов. “Перспектива”. Ротапринт ТДПУ имени Низами. Ташкент, 2006







