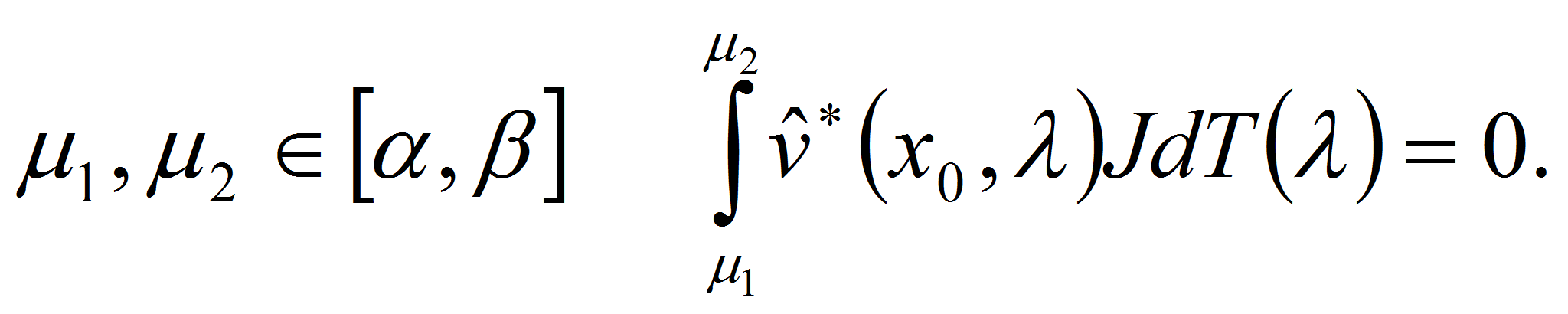Получены оценки ранга спектральной матрицы-функции самосопряженных расширений симметрического дифференциального оператора второго порядка, действующего в пространстве конечномерных вектор-функций, суммируемых с квадратом модуля.
Одной из фундаментальных проблем спектральной
теории линейных дифференциальных операторов является исследование их
спектральных характеристик в терминах коэффициентов соответствующих
дифференциальных операций [1]. Пусть
![]() - самосопряженный оператор, действующий в гильбертовом пространстве
- самосопряженный оператор, действующий в гильбертовом пространстве
![]() ,
порожденный формально самосопряженной дифференциальной операцией
второго порядка в пространстве вектор-функций. В этой заметке
сопоставляется ранг спектральной матрицы-функции оператора
,
порожденный формально самосопряженной дифференциальной операцией
второго порядка в пространстве вектор-функций. В этой заметке
сопоставляется ранг спектральной матрицы-функции оператора
![]() и кратность его спектра.
и кратность его спектра.
1. Предположим, что
![]() комплексная матричнозначная функция, заданная на всей числовой оси, и
комплексная матричнозначная функция, заданная на всей числовой оси, и
![]() - неотрицательная вещественнозначная мера, заданная на борелевской
- неотрицательная вещественнозначная мера, заданная на борелевской
![]() -
алгебре
-
алгебре
![]() подмножеств числовой прямой
подмножеств числовой прямой
![]() .
Если для любых
.
Если для любых
![]() и
и
![]()
![]() -
измеримы и интегрируемы по
-
измеримы и интегрируемы по
![]() ,
то будем считать, что
,
то будем считать, что
![]() и для любого измеримого подмножества
и для любого измеримого подмножества
![]()
![]() .
.
Предположим, что
![]() -
мерная, неотрицательно определенная, эрмитова, матричнозначная
функция, заданная на ограниченных борелевских подмножествах числовой
прямой, причем каждая функция
-
мерная, неотрицательно определенная, эрмитова, матричнозначная
функция, заданная на ограниченных борелевских подмножествах числовой
прямой, причем каждая функция
![]() - является счетно-аддитивной на семействе
- является счетно-аддитивной на семействе
![]() .
Матрица
.
Матрица
![]() задает положительную матричную меру. Каждая функция множества
задает положительную матричную меру. Каждая функция множества
![]() есть неотрицательная вещественнозначная мера и каждая
есть неотрицательная вещественнозначная мера и каждая
![]() при всех
при всех
![]() есть комплекснозначная мера. Поскольку для любой неотрицательной
эрмитовой матрицы
есть комплекснозначная мера. Поскольку для любой неотрицательной
эрмитовой матрицы
![]() ,
где
,
где
![]() - единичная матрица и
- единичная матрица и
![]() обозначает след, то каждая функция
обозначает след, то каждая функция
![]() - абсолютно непрерывна относительно меры
- абсолютно непрерывна относительно меры
![]() .
Матричную функцию
.
Матричную функцию
![]() обычно называют следовой производной от матричной меры
обычно называют следовой производной от матричной меры
![]() .
Матричная функция
.
Матричная функция
![]() - измерима по Борелю и интегрируема относительно
- измерима по Борелю и интегрируема относительно
![]() ,
причем
,
причем
![]() .
.
-
Пусть
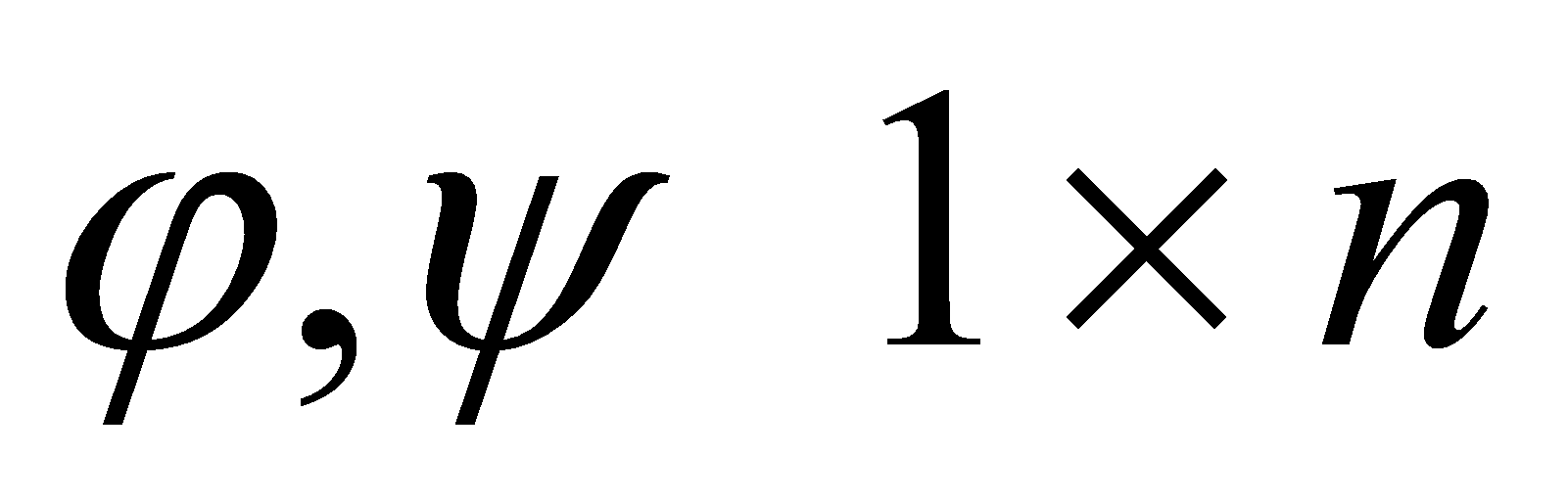 -
мерные векторнозначные функции на
-
мерные векторнозначные функции на
 .
Если
.
Если
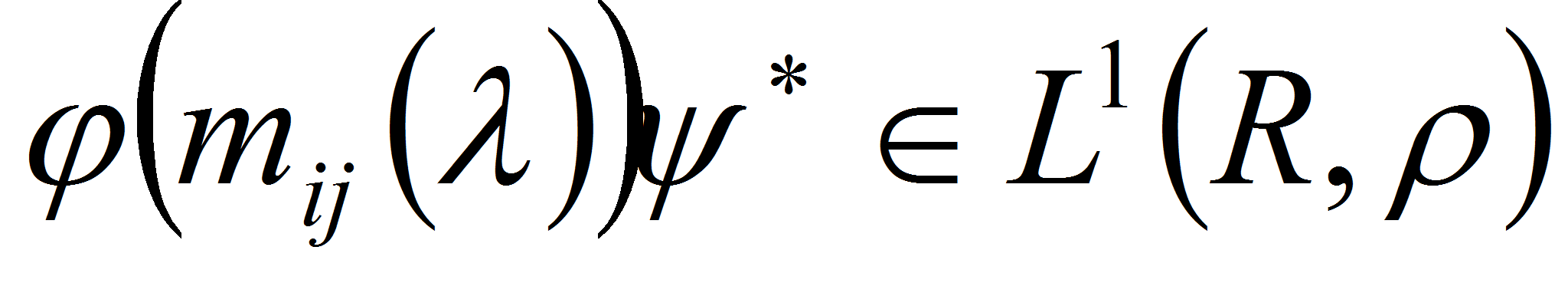 ,
то можно определить скалярное произведение следующим образом
,
то можно определить скалярное произведение следующим образом
Тогда
![]() обозначает класс всех измеримых по Борелю вектор-функций
обозначает класс всех измеримых по Борелю вектор-функций
![]() ,
заданных на всей числовой оси
,
заданных на всей числовой оси
![]() таких, что скалярные произведения
таких, что скалярные произведения
![]() существуют и конечны. Интеграл
существуют и конечны. Интеграл
![]() иногда записывают в виде
иногда записывают в виде
![]() .
.
![]() есть гильбертово пространство векторнозначных функций.
есть гильбертово пространство векторнозначных функций.
Пусть
![]() -
оператор умножения на независимую переменную в гильбертовом
пространстве
-
оператор умножения на независимую переменную в гильбертовом
пространстве
![]() ,
где
,
где
![]() - положительная матричная мера и область определения оператора
- положительная матричная мера и область определения оператора
![]() есть множество
есть множество
![]() .
.
Введем два гильбертовых пространства
![]() ,
в которых определены линейные операторы
,
в которых определены линейные операторы
![]() .
Унитарная эквивалентность между оператором
.
Унитарная эквивалентность между оператором
![]() из пространства
из пространства
![]() и
и
![]() из пространства
из пространства
![]() есть сохраняющее норму отображение
есть сохраняющее норму отображение
![]() из пространства
из пространства
![]() в пространство
в пространство
![]() ,
при котором
,
при котором
![]() отображается в некоторое множество
отображается в некоторое множество
![]() таким образом, что для любого
таким образом, что для любого
![]() имеет место соотношение
имеет место соотношение
![]()
![]() .
.
Определение 1. Две положительные матричные меры
![]() и
и
![]() не обязательно одинаковой размерности будем называть эквивалентными,
если существует унитарная эквивалентность между операторами умножения
на независимую переменную
не обязательно одинаковой размерности будем называть эквивалентными,
если существует унитарная эквивалентность между операторами умножения
на независимую переменную
![]() в пространстве
в пространстве
![]() и
и
![]() в пространстве
в пространстве
![]() .
.
Для
![]() -
мерной положительной матричной меры
-
мерной положительной матричной меры
![]() введем ее атомическую
введем ее атомическую
![]() и непрерывную
и непрерывную
![]() части, соответственно. Атом
части, соответственно. Атом
![]() есть любое множество, состоящее из отдельной точки
есть любое множество, состоящее из отдельной точки
![]() ,
такой что
,
такой что
![]() .
.
-
Пусть мера
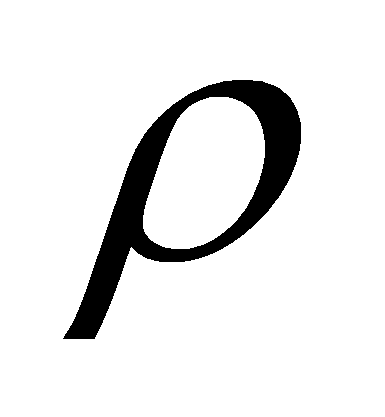 эквивалентна мере
эквивалентна мере
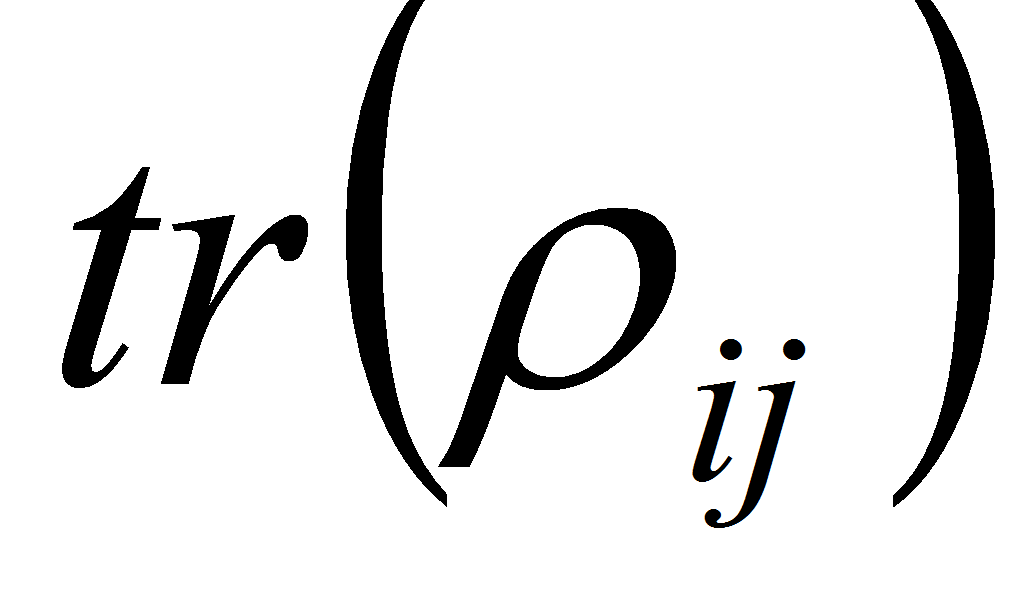 и пусть
и пусть
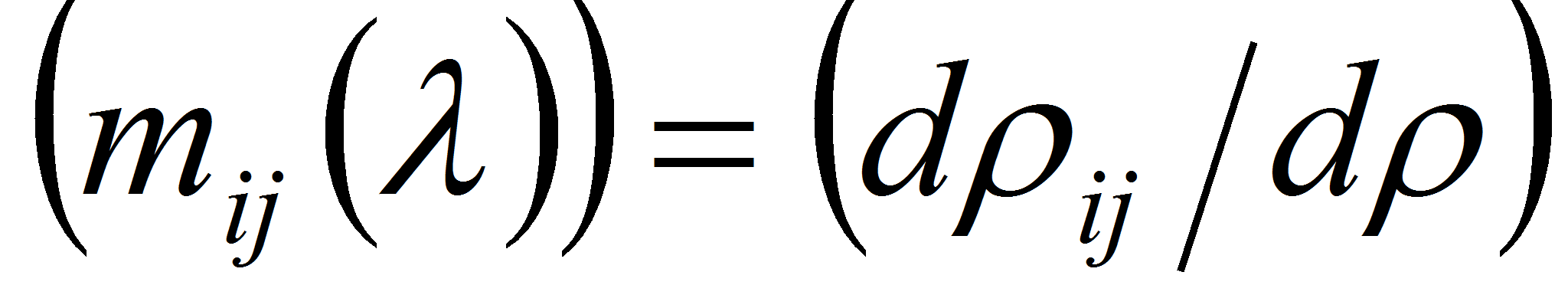 ,
тогда одномерная атомическая мера
,
тогда одномерная атомическая мера
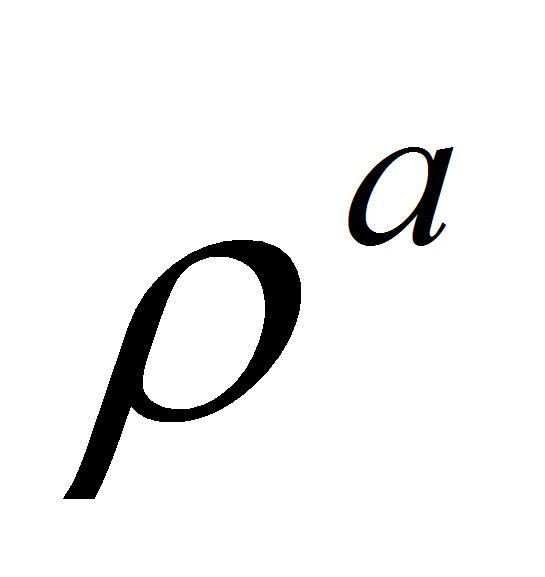 эквивалентна мере
эквивалентна мере
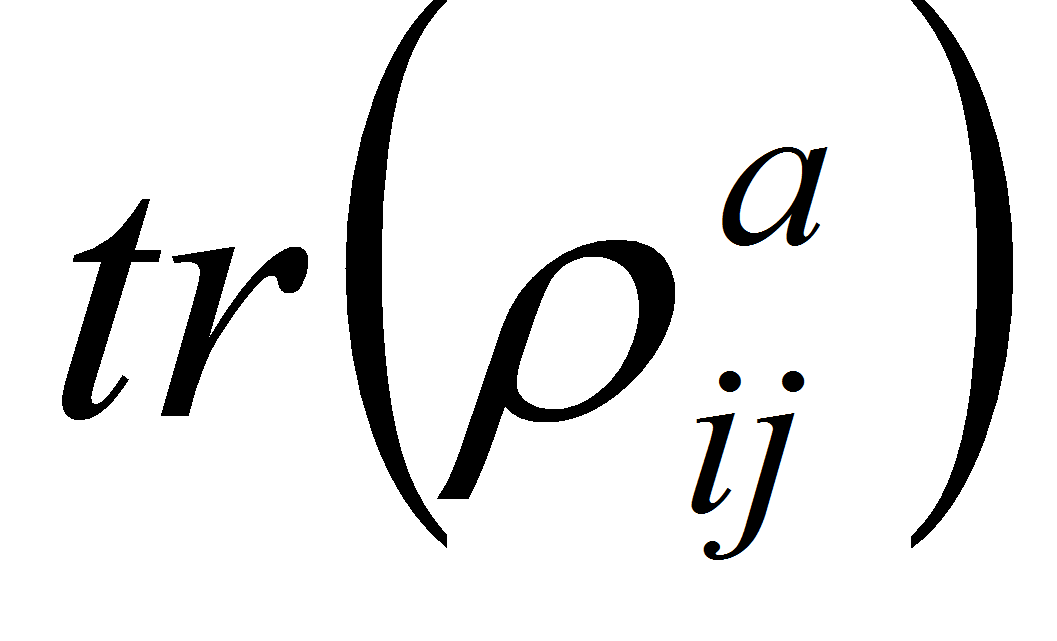 и
и
 ,
а одномерная непрерывная мера
,
а одномерная непрерывная мера
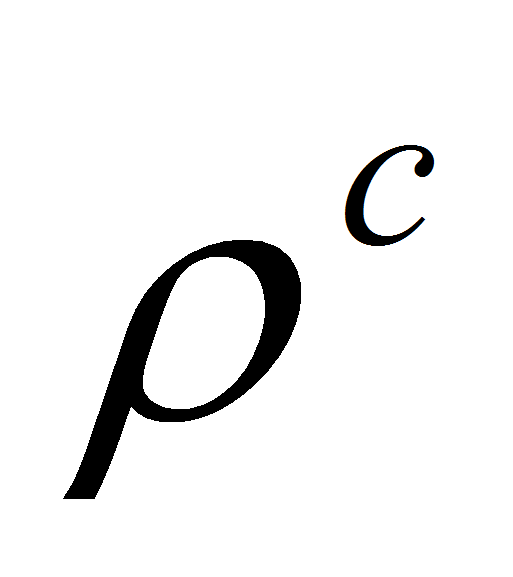 эквивалентна мере
эквивалентна мере
 и
и
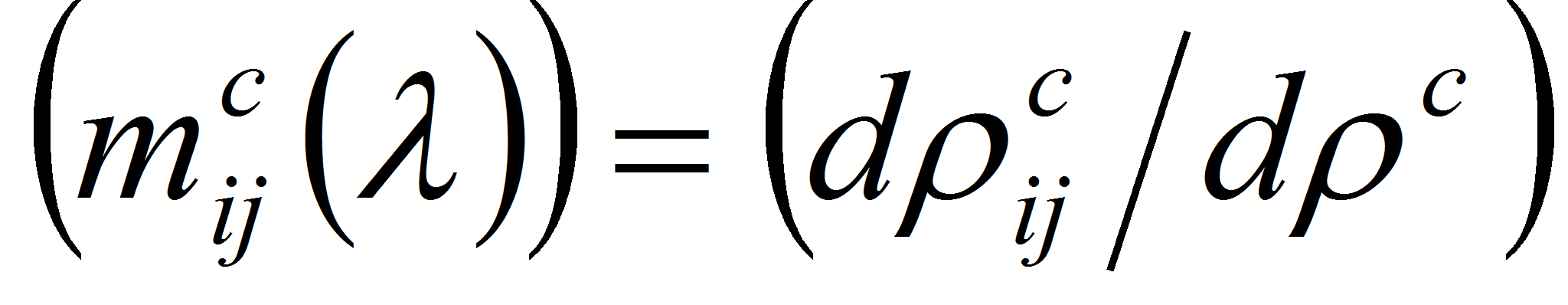 .
.
Для значений
![]() и
и
![]() пусть
пусть
![]() фиксированная
фиксированная
![]() -
мерная главная подматрица матрицы
-
мерная главная подматрица матрицы
![]() .
Детерминант
.
Детерминант
![]() есть
есть
![]() -
измеримая функция от переменной
-
измеримая функция от переменной![]() ,
следовательно, все множества
,
следовательно, все множества
![]() будут
будут
![]() -
измеримы и, кроме того, имеют место равенства
-
измеримы и, кроме того, имеют место равенства
![]() для значений
для значений
![]() .
.
Определение 2. Пусть
![]() - положительная матричная мера. Ранг
- положительная матричная мера. Ранг
![]() в точке
в точке
![]() обозначим символом
обозначим символом
![]() и определим соотношением
и определим соотношением
Атомический ранг
![]() в точке
в точке
![]() обозначим через
обозначим через
![]() .
Ранг непрерывной составляющей определим соотношением
.
Ранг непрерывной составляющей определим соотношением
Определение 3. Спектральная матрица для самосопряженного
оператора
![]() есть положительная матричная мера
есть положительная матричная мера
![]() ,
для которой существует унитарная эквивалентность между операторами
,
для которой существует унитарная эквивалентность между операторами![]() в пространстве
в пространстве
![]() и
и
![]() в
пространстве
в
пространстве
![]() .
.
Лемма 2. Если
![]() спектральная матрица для самосопряженного оператора
спектральная матрица для самосопряженного оператора
![]() и
и
![]() есть собственное значение
есть собственное значение
![]() кратности
кратности
![]() ,
то
,
то
![]() .
Если
.
Если
![]() не является собственным значением оператора
не является собственным значением оператора
![]() ,
то
,
то
![]() .
.
Теорема 1. Пусть
![]() -
кратность непрерывного спектра самосопряженного оператора
-
кратность непрерывного спектра самосопряженного оператора
![]() в точке
в точке
![]() .
Если
.
Если
![]() спектральная матрица, соответствующая оператору
спектральная матрица, соответствующая оператору
![]() ,
и
,
и
![]() ,
то
,
то
![]() .
.
2. Как известно, каждой спектральной функции
![]() минимального оператора
минимального оператора
![]() отвечает некоторая обобщенная резольвента
отвечает некоторая обобщенная резольвента
![]() ,
определенная формулой
,
определенная формулой
При помощи формулы обращения Стилтьеса спектральная функция
![]() однозначно восстанавливается по соответствующей ей обобщенной
резольвенте
однозначно восстанавливается по соответствующей ей обобщенной
резольвенте
![]() ;
для любых функций
;
для любых функций
![]() и
и
![]() из
из
![]() и любых вещественных
и любых вещественных
![]() и
и
![]() имеет место равенство:
имеет место равенство:
Равенство (1) позволяет построить формулу всех спектральных функций
![]() оператора
оператора
![]() по известной обобщенной резольвенте.
по известной обобщенной резольвенте.
3. Пусть выражение
![]() имеет вид
имеет вид
![]() ,
где
,
где
![]() - квадратная матрица-функция порядка
- квадратная матрица-функция порядка
![]() .
Кроме того,
.
Кроме того,
![]() измерима и локально суммируема в сильном смысле и при каждом
измерима и локально суммируема в сильном смысле и при каждом
![]() .
.
Выражение
![]() имеет смысл для каждой вектор-функции
имеет смысл для каждой вектор-функции
![]() ,
которая на любом отрезке
,
которая на любом отрезке
![]() абсолютно непрерывна вместе со своей первой производной и
абсолютно непрерывна вместе со своей первой производной и
![]() .
Скалярный случай рассмотрен в работах автора [2,
3].
.
Скалярный случай рассмотрен в работах автора [2,
3].
Каждой вектор-функции
![]() ,
для которой
,
для которой
![]() имеет смысл, поставим в соответствие вектор-функцию
имеет смысл, поставим в соответствие вектор-функцию
![]() .
Будем рассматривать
.
Будем рассматривать
![]() при любом
при любом
![]() как матрицу-столбец. Положим
как матрицу-столбец. Положим
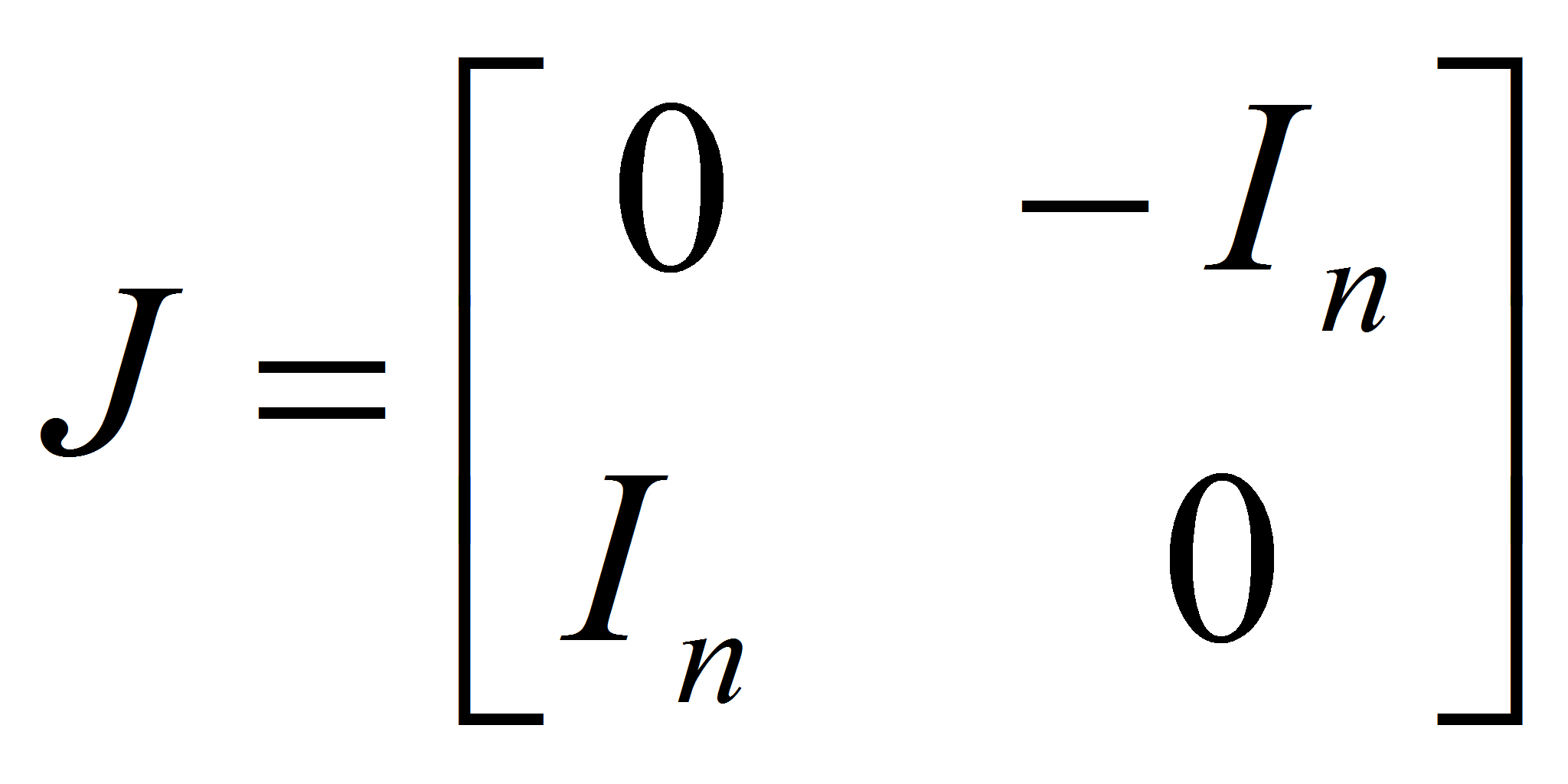 ,
где
,
где
![]() -
единичная матрица порядка
-
единичная матрица порядка
![]() .
Тогда аналог тождества Лагранжа примет следующий вид
.
Тогда аналог тождества Лагранжа примет следующий вид
![]() .
.
Через
![]() и
и
![]() обозначим фундаментальную систему решений матричного уравнения
обозначим фундаментальную систему решений матричного уравнения
![]() ,
удовлетворяющих начальным условиям
,
удовлетворяющих начальным условиям
где
![]() - произвольная фиксированная точка промежутка
- произвольная фиксированная точка промежутка
![]() .
.
Для любых вещественных
![]() и
и
![]() оператор
оператор
![]() является интегральным, а его ядро
является интегральным, а его ядро
![]() - представимо в виде
- представимо в виде
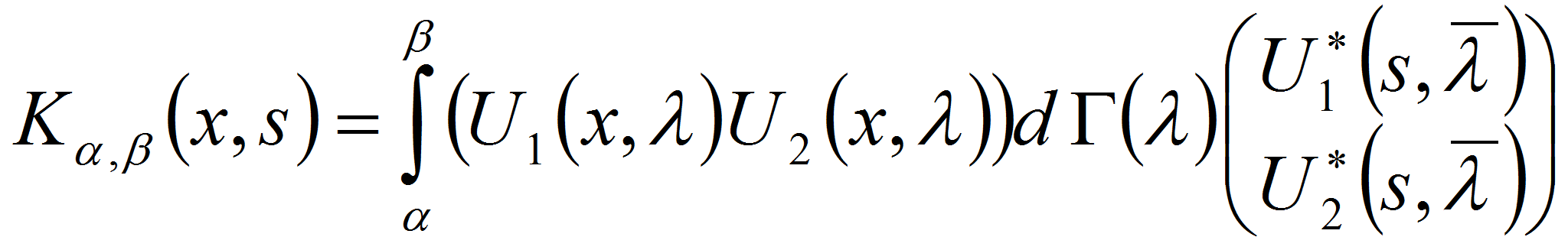 ,
где
,
где
![]() - эрмитово неубывающая матрица-функция порядка
- эрмитово неубывающая матрица-функция порядка
![]() ,
называемая спектральной функцией распределения оператора
,
называемая спектральной функцией распределения оператора
![]() .
.
Лемма 3. Пусть для любого
![]() уравнение
уравнение
![]() имеет решение
имеет решение
![]() такое, что:
такое, что:
1)
![]() ,
где
,
где
![]() какая-либо внутренняя точка промежутка
какая-либо внутренняя точка промежутка
![]() ;
;
3) для фиксированного
![]() вектор-функция
вектор-функция
![]() удовлетворяет условию Липшица относительно
удовлетворяет условию Липшица относительно
![]() на сегменте
на сегменте
![]() .
.
Теорема 2. Пусть при любом
![]() уравнение
уравнение
![]() имеет
имеет![]() линейно независимых решений
линейно независимых решений
таких, что:
б)
 какова бы ни была вектор-функция
какова бы ни была вектор-функция
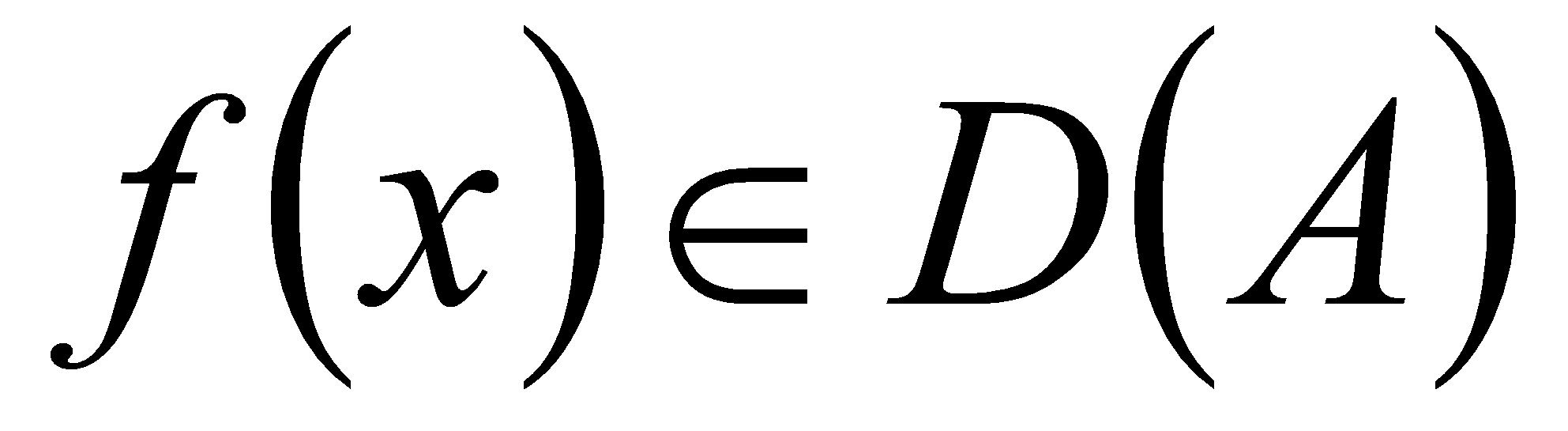 ;
;3) каждая из вектор-функций
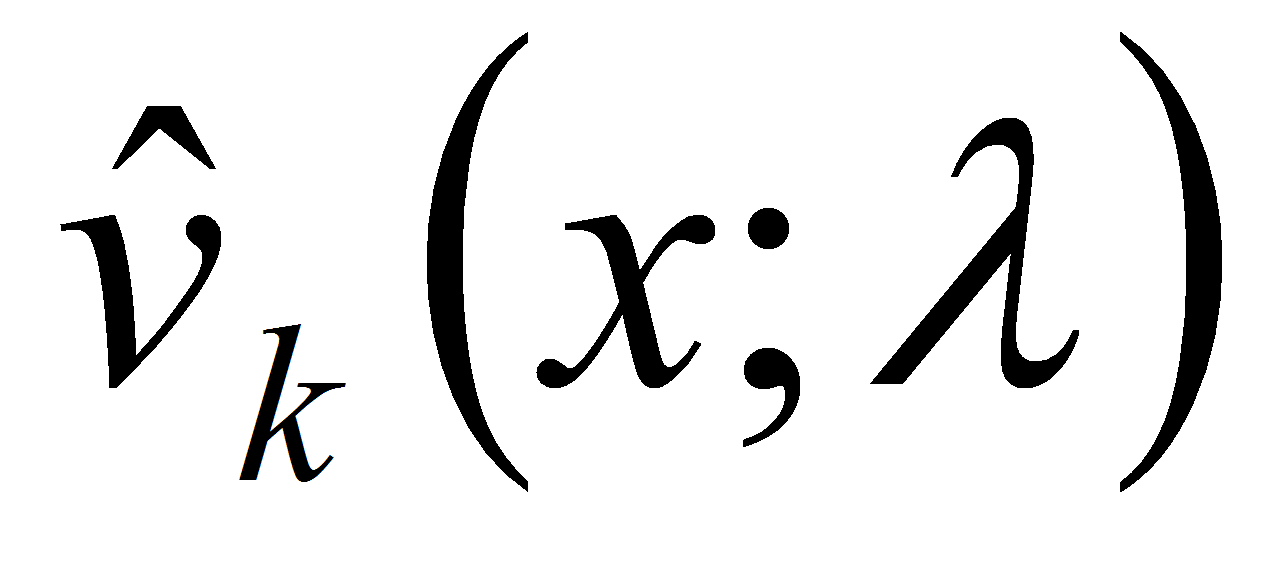 при любом фиксированном
при любом фиксированном
 удовлетворяет условию Липшица по переменной
удовлетворяет условию Липшица по переменной
 на сегменте
на сегменте
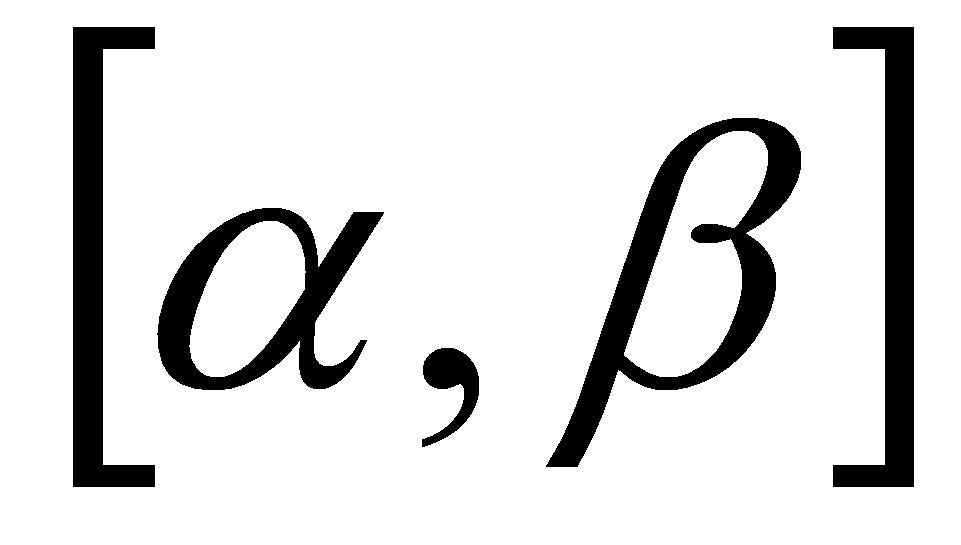 .
.
Тогда кратность части спектра оператора
![]() ,
заключенной в сегменте
,
заключенной в сегменте
![]() ,
не превосходит
,
не превосходит
![]() .
.
Замечание 1. Если какой-либо из операторов с
минимальной областью определения, порожденных операцией
![]() в пространствах
в пространствах
![]() и
и
![]() имеет индекс дефекта
имеет индекс дефекта
![]() ,
то можно опустить условие 1 б) или 2 б), так как его выполнение
обеспечивается в этом случае условием 1 а) или 2 а).
,
то можно опустить условие 1 б) или 2 б), так как его выполнение
обеспечивается в этом случае условием 1 а) или 2 а).
Замечание 2. В условиях теоремы 2 ранг матрицы
![]() не превосходит
не превосходит
![]() .
.
-
- Литература:
Наймарк М.А. Линейные дифференциальные операторы. – М.: Наука, 2010. – 528 с.
Филиппенко В.И. Оценка кратности спектра квазидифференциального оператора // Исследования по математическому анализу, математическому моделированию и информатике. – Владикавказ: Владикавказский научный центр РАН и РАО - А, 2007. – С. 86 – 93.
Фетисов В.Г., Филиппенко В.И., Козоброд В.Н. Операторы и уравнения в линейных топологических пространствах. – Владикавказ: ВНЦ РАН, 2006. – 432 с.