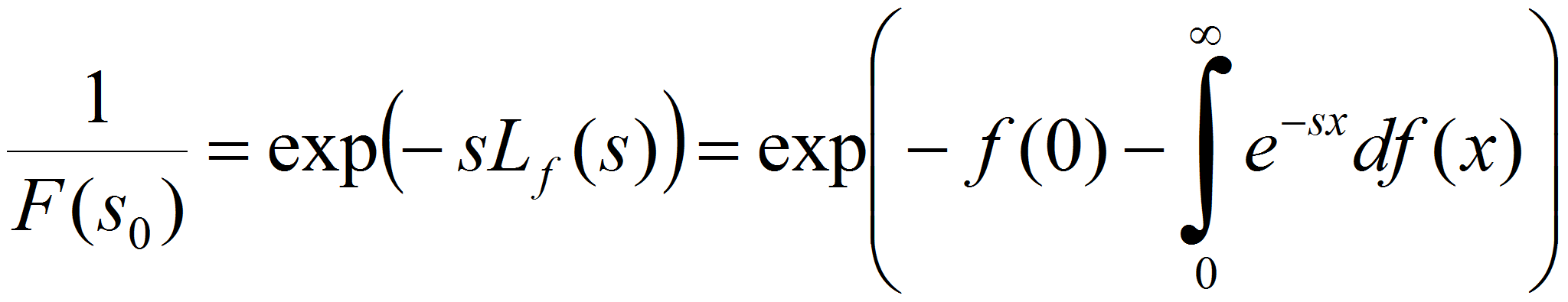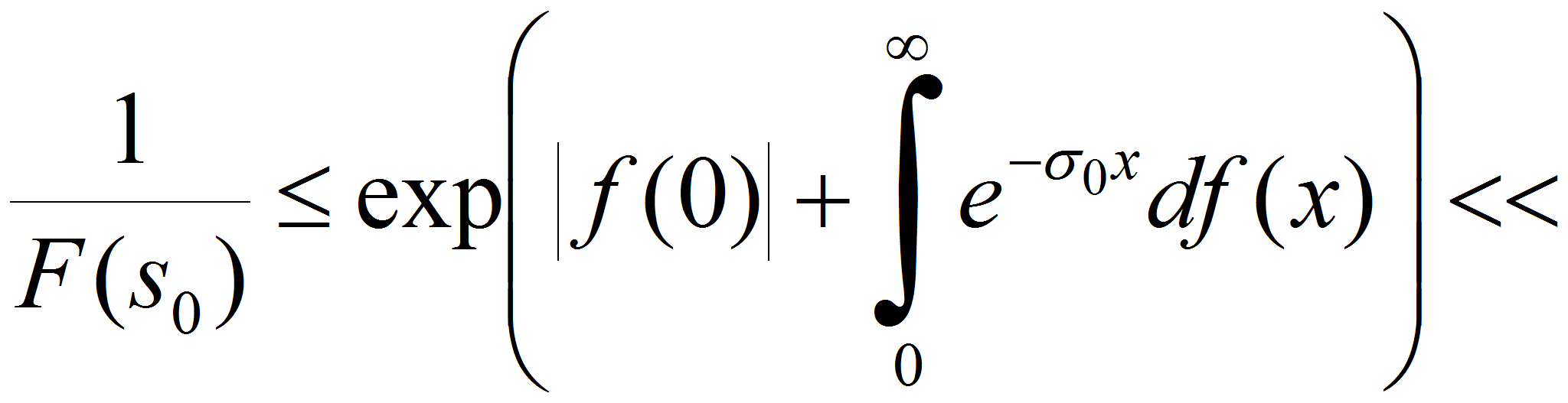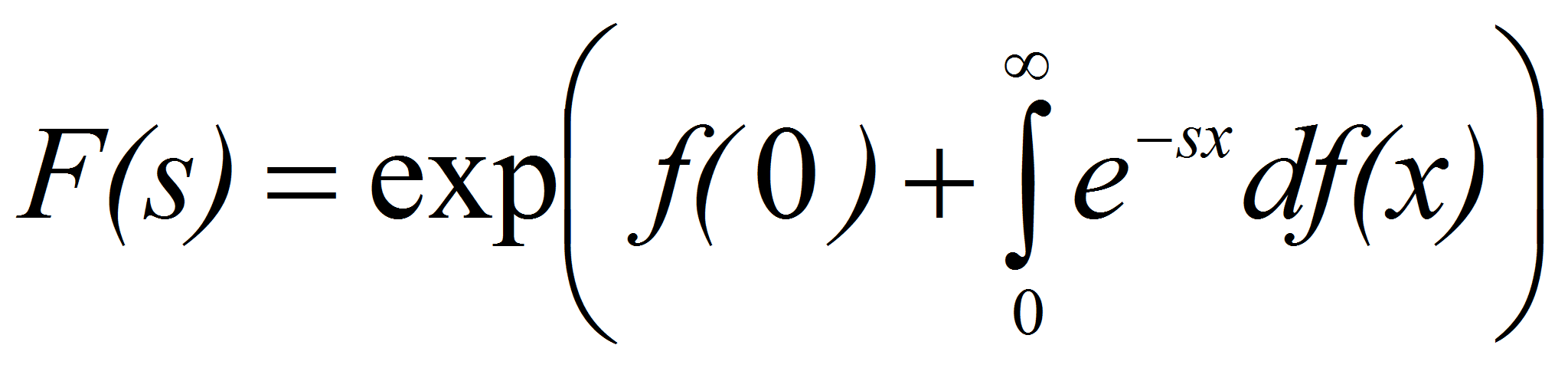В работе доказывается, что если полуплоскости сходимости преобразование Лапласа некоторой неубывающей функции близко к экспоненте преобразования Лапласа другой неубывающей функции и допускает аналитическое предложение в некоторую вертикальную полосу левее абсциссы сходимости, то оно не обращается в нуль в области, подобной области Валле-Пуссена, свободной от нулей дзета- функции.
In the work it is proved that if in a half plane of convergence the transformation of Laplasa of some nondecreasing function is close to an exponent of transformation of Laplasa of other nondecreasing function and supposes analytical continuation in some vertical strip more to the left of a convergence absciss thus it does not turn to zero in the area similar to area of Valle-Pussen free from zeta-function zero.
Классическая
постановка задачи о распределении простых чисел в натуральном ряду
состоит в исследовании асимптотического поведения функции
означающий число простых чисел, не превосходящих
Известные в настоящее время
асимптотические формулы для
имеют вид
где
интегральный
логарифм, а
- остаточный член, оценка которого связана с распределением нулей
дзета функции Римана:
Согласно теореме Валле-Пуссена
где
- положительная константа.
Лучший из
известных в настоящее время результатов принадлежит Виноградову и
Коробову и состоит в том, что указатель
можно заменить на
,
где
- произвольное малое положительное число. Первым шагом в
доказательстве этих оценок является классическое тождество Эйлера
справедливое
в полуплоскости
Используя элементарные сведения о простых числах из тождества Эйлера нетрудно получить, что
где
- функция регулярное и ограниченная в полуплоскости
С другой
стороны в полуплоскости с
и аналогично
введем обозначение
преобразование
Лапласа функции
определенной для всех неотрицательных
и интегрируемой на каждом конечном отрезке
Тогда из тождества Эйлера следует:
(1)
при
Таким
образом, задача о распределении простых чисел является частным
случаем следующей общей задачи: заданы две функции вещественного
аргумента
и
,
преобразования Лапласа которых связаны соотношением (1), причем
функция
устроена достаточно хорошо.
Считая
асимптотику функции
известной, найти асимптотику функции
.
В
дальнейшем мы будем считать что при
(2)
где
- положительная константа.
Отсюда следует, что преобразование Лапласа
абсолютно
сходится в полуплоскости
.
При этом
для любого
в полуплоскости
сходимость равномерна и поэтому функция
регулярна в полуплоскости
.
Из формулы
(2) следует, что функция
аналитически продолжается в полуплоскость
,
из которой удалена точка
в этой же точке функция
имеет простой полюс с вычетом равным
Действительно, так как
где
то
Из оценки
непосредственно следует, что преобразование Лапласа
сходится абсолютно в полуплоскости
и равномерно в полуплоскости
для любого
Отсюда
вытекает, что функция
регулярна в полуплоскости
.
В
дальнейшем мы полагаем
так что
Лемма
1.
Пусть
в условиях (1) и (2)
неубывающая функция и
для
Тогда
функция
не обращается в нуль на прямой
=
1.
Доказательство. Введем обозначение
Тогда из (1) следует
Так как
то показатель степени равен
Поскольку
для всех действительных
.
Таким
образом, если
для действительных
то для любого действительного
(3)
С другой
стороны, пусть
- нуль функции
кратности
Тогда
при
Так как
стремится к конечному пределу при
и
при
,
то
т.е.
при
в противоречии с неравенством (3). Лемма доказана.
Лемма
2.
Для
любого
из условия (2) следует, что при
справедливо оценка
Действительно,
Так как
то при
имеем:
Для дальнейшего нам понадобится следующие теоремы Ландау [1]
Теорема
А.
Пусть функция
регулярна в круге
и удовлетворяет в нём неравенству
(4)
Тогда
(5)
где
- пробегает нули функции
в круге
Теорема
B.
Пусть функция
удовлетворяет условиям теоремы А и кроме того не обращается в нуль в
области
где
.
Тогда если
(6)
где
- постоянная, то в круге
справедлива неравенство
,
(7)
где
- постоянная.
Применим
теорему A
к функции
и кругу радиуса
с центром в точке
где
такова, что точка
есть нуль функции
причем
Будем
считать, что
тогда точка
находится в круге
Из неравенства (5) следует
Откуда
(8)
Так как
функция
не обращается в нуль в полуплоскости
и
,
то все слагаемые последней суммы неотрицательные, и она может только
уменьшится если мы отбросим все слагаемые кроме одного в котором
Следовательно,
(9)
Выясним
теперь, что в наших условиях можно взять в качестве
Так как
круг
ввиду
находится от точки
на расстоянии >2, то в этом круге по лемме 2.
и
(при
условии, что функция
ограничена в полуплоскости
).
Далее
Откуда
Поэтому в
круге
справедлива оценка
Следовательно,
функция
в круге
удовлетворяет условиям теоремы А при
где
абсолютная константа.
Поэтому из неравенства (6.8) следует
Применим теперь теорему А к той же функции
и кругу
радиуса
с центром в точке
,
где
и
определены так же, как и выше.
Поскольку в неравенстве
где
- пробегает нули функции
в
круге
все слагаемые суммы справа неотрицательны, то
Используя
лемму2. как и выше получаем, что в качестве
можно взять величину
где
абсолютная константа. Поэтому
Кроме того,
Откуда
следует, что функция
имеет при
простой полюс с вычетом –1.
Следовательно,
при
справедливо неравенство
Отсюда и из предыдущих неравенств вытекает:
(10)
С другой
стороны, при
ввиду равенства
имеем:
Откуда следует
так как
- неубывающая функция. Сопоставляя это с неравенством (6.10),
получаем
До сих пор
и
- произвольные положительные числа с условием
Положим
теперь
Тогда из предыдущего неравенства следует
Пусть
,
тогда выражение в скобках положительно. Так как
и
то отсюда следует:
Последнее
неравенство показывает, что
где
- положительная константа, зависящая только от
.
Действительно, при достаточно малых
левая часть неравенства положительна, так как она стремиться к
,
когда
Вспоминая определение
,
получаем следующий результат:
Теорема
1.
Пусть
и
- функции определенные при
причем
- неубывающая функция,
где
функция
- такова, что
ограничена в полуплоскости
Тогда, если
то функция
не обращается в нуль в области
где
- положительная константа, зависящая только от
.
Литература:
Landau E. Über den verlauf der zahlentheorethen Funktion. Arch. Math. und Phys. 5 (1903), 86-91.
Ингам А.Е. Распределение простых чисел.- ОНТИ, 1936.
Тичмарч Е. Теория дзета функции Римана, ИЛ, 1953.
