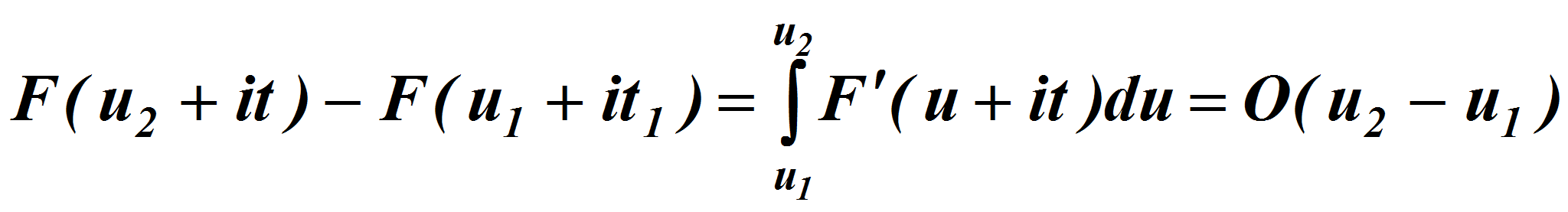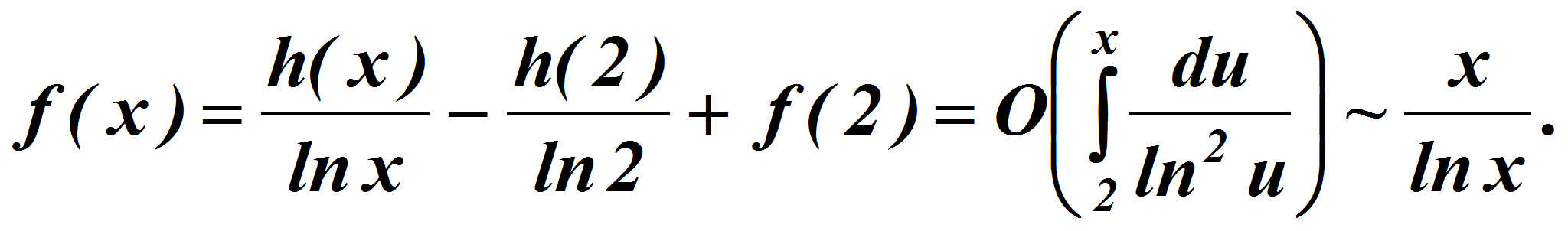Непрерывные аналоги закона распределения простых чисел

Рубрика: 14. Общие вопросы технических наук

Опубликовано в

международная научная конференция «Современные тенденции технических наук» (Уфа, октябрь 2011)

Статья просмотрена: 53 раза

Библиографическое описание:

Оразов, Мамед. Непрерывные аналоги закона распределения простых чисел / Мамед Оразов. — Текст : непосредственный // Современные тенденции технических наук : материалы I Междунар. науч. конф. (г. Уфа, октябрь 2011 г.). — Уфа : Лето, 2011. — С. 76-77. — URL: https://moluch.ru/conf/tech/archive/5/958/ (дата обращения: 20.04.2024).

Работа содержит достаточные условия, которым должно удовлетворять преобразование Меллина неубывающей функции , чтобы была справедлива асимптотическая формула при . Из полученных результатов, в частности, при здесь содержится асимптотический закон распределения простых чисел.

Work contains sufficient conditions with which should satisfy transformation Меllin of not decreasing function that it was fair Asymptotic formulae at . From the received results, in particular, at here contains asymptotic the law of distribution of simple numbers.

Пусть − неубывающая функция, определенная при

Поставим вопрос о том, какие минимальные ограничения на функцию обеспечивают асимптотическую формулу

− аналог закона простых чисел.

В работе доказывается следующая лемма.

Лемма 1. Пусть интеграл сходится при ,. Если производная равномерно продолжима на прямую , исключая точку ,

при , то функция не обращается в нуль в замкнутой полуплоскости .

Мы воспользовались тем, что из равномерной продолжимости следует равномерная продолжимость , так как при

что влечет за собой равномерную продолжимость функции , и следовательно, оценку

Далее из равенства следует

Функция очевидно неубывающая.

Применим к ней сформулированную ниже теорему Икеара.

Теорема. (Теорема Икеара [2]). Пусть неубывающая функция, определенная при .

Если функция

равномерно продолжима на прямую , то при .

В нашем случае

так что из предыдущего вытекает, что условия теоремы Икеара выполнены. Согласно этой теоремы

Отсюда следует

откуда

Теорема доказана.

Литература:

Ингам А.Е. Распределение простых чисел.− ОНТИ, 1936.
Райков Д.А. Обобщение теоремы Икеара−Ландау.− Матем. сб. 8(45), №3, 1938, 559-568.
Постников А.Г. Упрощение элементарного доказательства А.Сельберга асимптотического закона распределения простых чисел.− УМН, т.х., 1955, №4.

Основные термины (генерируются автоматически): неубывающая функция, асимптотическая формула, теорема, функция.

Похожие статьи

О нулях преобразовании Лапласа некоторых неубывающих...

неубывающая функция, функция, асимптотика функции, положительная константа.

Основные термины (генерируются автоматически): неубывающая функция, функция, теорема, асимптотическая формула.

(Теорема Икеара [2]). Пусть неубывающая функция...

функция, неубывающая функция, прямая, теорема, асимптотическая формула.

Теорема Карамата и её применение в аддитивных задачах

Положим ; функция h(t) неубывающая, так как и . Согласно теореме Карамата [2], при.

Таким образом, если , то справедливость асимптотической формулы (6) обеспечивается уже просто редкостью последовательности V. Арифметическая природа членов этой последовательности...

О нулях преобразований Лапласа некоторых неубывающих...

Известные в настоящее время асимптотические формулы для имеют вид.

Теорема 1. Пусть и - функции определенные при причем - неубывающая функция, где функция - такова, что 1/ ограничена в полуплоскости.

Соотношение между усредненными модулями гладкости функции...

, . Известно, что - неотрицательная, неубывающая, непрерывная функция и.

Наилучшее приближение функции множеством определяется по формуле.

Теорема 1 ([2]). Пусть , и , . Тогда для функции справедлива оценка.

Об асимптотическом поведении решений систем нелинейных...

уравнение, неизвестная функция, система, система вида, теорема, условие теоремы. Построение асимптотических решений системы нелинейных дифференциальных уравнений нейтрального типа.

Использование функции Грина в прикладной механике

Через здесь обозначена неубывающая на отрезке функция, определяющая распределение масс.

Последняя формула означает, что является функцией Грина задачи (5).

Теорема 2. Функция удовлетворяет указанным выше соотношениям тогда и только тогда.

Существенный спектр модельного трехчастичного оператора...

. Следующая теорема описывает местоположение существенного спектра оператора .

Уравнение Вайнберга для собственных функций модельного... Рассмотрим модельный оператор , действующий в гильбертовом пространстве по формуле. , где операторы...

О некоторых задачах теории мультипликативных функций

Доказывается следующие теоремы: Теорема 1. Пусть и − неотрицательные мультипликативные функции, причем для всех .

Файнлейб А.С. Некоторые асимптотические формулы для сумм мультипликативных функций и их приложения.&# ; Литовский матем. сборник, 7, №13, 1967...