Пусть задано следующее уравнение 2-го порядка с двумя переменными в области 
:
(1)
Здесь 
— коэффициенты уравнения, определенные в области достаточно гладкие функции, одновременно в 
не равные нулю, а 
заданная функция своих аргументов.
Введем следующее обозначение: 
.
Мы знаем, что в области значение выражения 
может быть отрицательным, положительным или равным нулю, тогда соответственно в уравнение (1) называется или эллиптического, или гиперболического, или параболического типа.
Для изучения физического процесса кроме уравнения определяющий этот процесс, должны быть заданы дополнительные условия, т. е. начальные и граничные условия. С точки зрения математики это связано с неединственностью решения дифференциального уравнения.
Для нахождения решения задачи, определяющего физический процесс, нам приходиться задать дополнительные условия. Пусть 
область, где происходит процесс, а 
её граница, она частично гладкая поверхность. Для дифференциальных уравнений различают три типа задач: задача Коши; краевая задача; смешанная задача.
Мы знаем, что свободное колебание струны задается следующим уравнением:
.(2)
Общее решение этого уравнения имеет следующий вид:
Используя это решение, мы можем решить задачу Коши.
Задача Коши: Найти решение уравнение (2) в области 
, удовлетворяющее начальные условия:
,
. (3)
Решения задачи Коши задается формулой Даламбера:
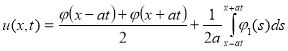. (4)
В полуограниченной 
области для уравнение (2) мы можем ставить следующие краевые задачи; т. е. в области 
мы должны найти 
функцию, решение задачи (2)-(3), удовлетворяющее, или 
(I краевое условие), или 
(II краевое условие), или 
(III краевое условие) граничное условие. Эти задачи соответственно называются или первой краевой задачей, или второй краевой задачей, или третьей краевой задачей.
Для решения таких задач используем метод продолжений. Здесь функция продолжается или на четную, или на нечетную функцию. Если начально- заданные функции относительно 
нечетные, тогда 
, если начально- заданные функции относительно четные, тогда 
. Мы используем эти факты при решения задач, заданных в полуограниченных областях для уравнений гиперболического типа.
Теперь рассмотрим в полуограниченной области задачу для уравнения теплопроводности:
, , 
,(5)
.(6)
Для решения задач поставленных для уравнений теплопроводности в полуограниченной области мы можем использовать следующие леммы.
Лемма 1. Если в определенная функция 
относительно точки 
нечетная, тогда решение задачи (5), (6) в точке равно нулю, т. е. 
.
Доказательство. Для доказательства этой леммы, мы используем следующую формулу Пуассона для решения задачи (5), (6):
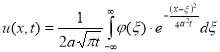.(7)
Находим значения функции 
при :
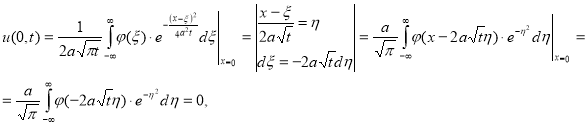
т. е., по условию леммы 
— нечетная функция, а мы знаем, 
— четная функция. Произведение четных и нечетных функций есть нечетная функция, по свойству определенного интеграла в симметрической области определенный интеграл от нечетной функции равен нулю, значить и наш интеграл тоже равен нулю. Лемма доказана.
Лемма 2. Если в определенная функция относительно точки четная, тогда производная по 
от решения задачи (5), (6) в точке равен нулю, т. е. 
.
Доказательство этой леммы проводится, как предыдущая лемма.
Используя эти леммы, мы можем решить задачи, поставленные для уравнений параболического типа в полуограниченных областях.
Литература:
- Салохиддинов М. С., Математик физика тенгламалари. Т. «Ўзбекистон». 2002. — 448 б.
- Жўраев Т. Ж., Абдиназаров С. Математик физика тенгламалариТ., 2003
- Бицадзе А. В. Уравнения математической физики. М., Наука 1976.
- Тихонов А. Н., Самарский А. А. Уравнения математической физики. М. 1968.
