В данной статье рассматривается возможность выигрыша в азартной игре под названием «Рулетка» с точки зрения теории вероятностей. Приводятся рассуждения, подтверждающие основную гипотезу о «практической невозможности» выигрыша в азартные игры на длинной дистанции.
Ключевые слова: вероятность, теория игр, рулетка, математическое ожидание.
Введение
Множество естественных наук опирается на вероятностные методы. На самом деле, первые труды ученых-математиков, посвященные теории вероятности как науке, объектом исследования и изучения принимали выявление закономерности и возможности предвидения исхода азартных игр. Подобная наука не определяет точного результата игры, а лишь дает оценку возможностям и шансам игроков. Раздел математики, изучающий выбор оптимальных стратегий в конфликтных ситуациях, в рамках которых идет борьба между участниками, называется «Теория игр». Математика позволяет просчитать вероятности победы в игре и выработать стратегии. Но значит ли это что, зная математику, а в частности теорию вероятности можно выигрывать в азартных играх? Разберем основные понятия теории вероятности и как она применяется в играх.
- Основные понятия теории вероятностей
- Случайное событие — явление, о котором имеет смысл говорить, что оно происходит или не происходит.
- Достоверное событие — событие которое обязательно произойдёт при осуществлении определённой совокупности условий.
- Невозможное событие — событие которое никогда не произойдёт при определённой совокупности условий.
- Единственное возможное событие — события называют единственно возможными, если наступление одного из них — это событие достоверное.
- Равновозможные события — события называют равновозможными, если ни одно из них не является более возможным, чем другие.
- Совместимые и несовместимые события — два события называются несовместимыми, если появление одного из них исключает появление другого. В противном случае события называются совместимыми.
-
Классическое определение вероятности: Вероятностью события
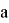
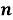
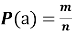
- Основные формулы комбинаторики [1]:
— Число перестановок
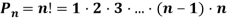
— Число размещений Anm=n⋅(n−1)⋅...⋅(n−m+1);
— Число сочетаний
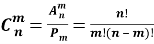
- Математическое ожидание случайной величины X (обозначается M(X) характеризует среднее значение случайной величины [2].
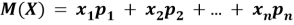
- Применение теории вероятности в азартной игре
Математическое ожидание в рулетке
Рулетка — азартная игра, которая представляющая из себя вращающееся колесо с 37 секторами, 18-черных секторов, 18-красных и один сектор зеленый-зеро. Игроки, играющие в рулетку, могут сделать ставку на выпадение цвета (красного или черного), числа (чётного или нечётного), диапазона (1–18 или 19–36) или конкретного числа. Также существует и другие ставки.
Существует множество «выигрышных» стратегий игры в рулетку, одна из самых популярных — это стратегия Мартингейла (удвоения), при которой игрок делает ставки только на один цвет [1]. При этом после каждого проигрыша ставка удваивается, после выигрыша ставка возвращается к первоначальной. Минус этой стратегии состоит в том, что во всех казино стоит ограничение по ставке, иными словами, при очередном проигрыше не получится удвоить ставку. Все остальные стратегии также терпят неудачу, при применении формулы математического ожидания. Применяя к игре математическое ожидание является суммой, которую вы можете заработать или проиграть в среднем по каждой ставке.
Рассчитаем математическое ожидание при различных ставках. Ставка всегда равна 1. Х — величина выигрыша или проигрыша; Р(х) — вероятность.
Ставка на цвет:
|
Х |
1 |
-1 |
|
Р(х) |
18/37 |
19/37 |

Ставка на число:
|
Х |
35 |
-1 |
|
Р(х) |
1/37 |
36/37 |

Ставка на пару чисел
|
Х |
17 |
-1 |
|
Р(х) |
2/37 |
35/37 |
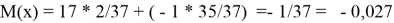
Во всех случаях математическое ожидание отрицательное. Правила игры созданы так, что с повышением вероятности того, что произойдёт определённое событие, уменьшается ставка на это событие, при этом математическое ожидание остаётся неизменным.
- Заключение
Знание математики определенно помогает при игре в азартные игры, но даже умело просчитывая вероятность проигрыша и победы не получится всегда быть в плюсе. Выигрыши в казино бывают, но это случайные события, которые невозможно гарантированно повторить. Желание увеличить прибыль приводит к погоне за следующей удачей, и в этой погоне на ставках люди теряют все деньги, включая выигранные. А всё потому, что чем больше ставок делает игрок, тем сильнее работает математическое ожидание в пользу казино и тем быстрее он проигрывает. Всегда длительная игра в азартные игры приводит к проигрышу в независимости от знаний математики и удачи.
Литература:
- Шклярник. В. С. Введение в комбинаторику и теорию вероятностей. Учеб. пособие, изд.. второе, исправ. и доп. СПб., ЛОИРО, 2017
- Кретов М. В. Теория вероятностей и математическая статистика: учебное пособие — Калининград: Янтарный сказ, 2004.

