Математическая модель анализа результатов футбольных матчей

В статье авторы приводят описание математической модели анализа результатов футбольных матчей для нескольких статистических характеристик.

Ключевые слова: статистика, математика, медиана, мода, размах.

В современном мире накапливается все больше и больше разнообразной информации. Мы все глубже погружаемся в бездну информационного пространства. Чтобы исправить эту ситуацию, общество обрабатывает и структурирует данные. Статистическая обработка данных позволяет нам увидеть закономерности, тенденции и отклонения в данных. Позволяет проводить сравнения, делать выводы и принимать решения на основе имеющейся информации. Она также позволяет проверять гипотезы, определять степень связи между переменными и оценивать статистическую значимость полученных результатов. В целом, статистическая обработка данных является важным инструментом для исследования и понимания различных явлений и процессов.

Футбол — один из самых популярных и массовых видов спорта в мире. Анализируя игру футболистов с помощью статистических методов, тренеры спортсменов могут прогнозировать результаты будущих матчей, улучшать спортивную подготовку футболистов. Это так же полезно для аналитиков, букмекеров и болельщиков футбола.

Изучение футбольной статистики имеет большую актуальность в современном спортивном мире.

Перечислим наиболее важные причины применения статистических методов для принятия решений в спорте и, в частности, в футболе:

1. анализ команды: футбольная статистика позволяет тренерам и аналитикам детально изучить прошлые матчи и выявить сильные и слабые стороны команды. Это помогает им разрабатывать стратегии и тактику для улучшения игры;
2. подготовка к матчу: изучение статистики позволяет командам анализировать стиль игры своих соперников, их сильные и слабые стороны, чтобы разработать оптимальный план для победы. Знание статистики может дать команде преимущество в предстоящих матчах;
3. поиск талантов: анализ футбольной статистики помогает скаутам и тренерам выявлять и привлекать талантливых игроков. Путем анализа статистики можно увидеть, какие игроки проявляют выдающиеся навыки и способности, что помогает при принятии решений о подписании контрактов;
4. тактический анализ: футбольная статистика помогает тренерам и командам анализировать эффективность различных тактик и систем игры. Они могут исследовать, какие стили игры наиболее успешны и эффективны в определенных ситуациях;
5. прогнозирование результатов: изучение футбольной статистики позволяет создавать модели и прогнозировать результаты матчей. Это может быть полезным для букмекерских контор, фанатов и аналитиков для определения вероятности победы определенной команды.

Рассмотрим математическую модель анализа статистики футбольных матчей на примере небольшой выборки первых 5-ти туров Российской премьер-лиги 2023–2024 гг. [1] на примере 4-х статистических показателей.

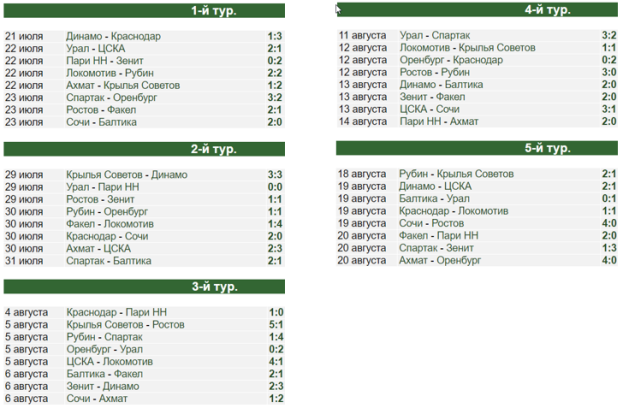
Рис. 1. Скриншоты результатов избранных футбольных матчей Российской премьер-лиги 2023–2024 гг.

1. Используя входную информацию (рис. 1), рассчитаем и запишем в табл. 1 количество забитых голов в каждом туре и матче.

Таблица 1

Количество футбольных турниров и результаты матчей в Российской премьер-лиге 2023–2024 гг.

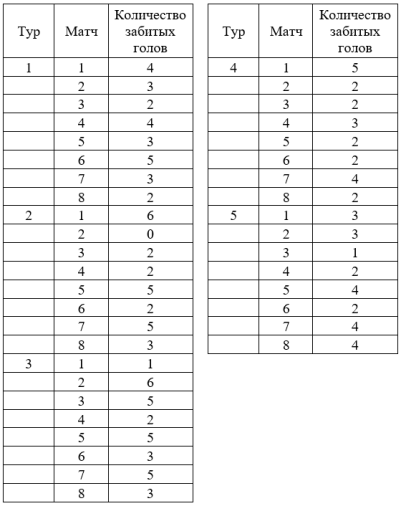
2. Проранжируем ряд с количеством забитых голов по всем матчам и для наглядности выделим цветом середину ряда (см. табл. 2).

Таблица 2

Ранжированный ряд количества забитых голов, забитых на Российской премьер-лиги 2023–2024 гг.

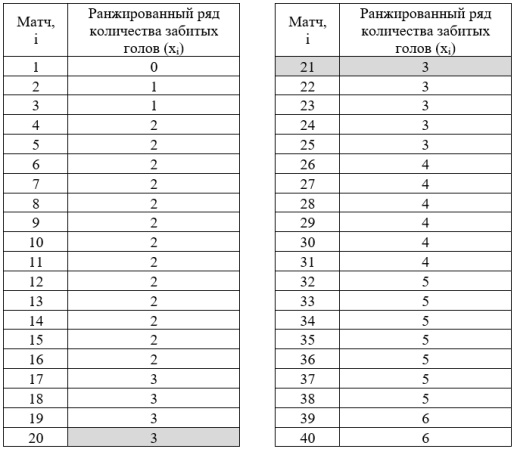
3. На основе данных из табл. 2 рассчитаем и построим табл. 3. В первом столбце запишем варианты количества забитых голов в одном матче, во втором — количество забитых голов в одном матче. В третьем столбце — количество матчей, в которых забит один из вариантов голов.

Таблица 3

Количество забитых голов в одном матче

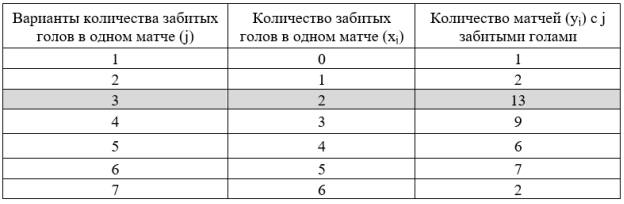
4. По данным табл. 3 построим гистограмму распределения (рис. 2) показателя «количества забитых голов в одном матче».

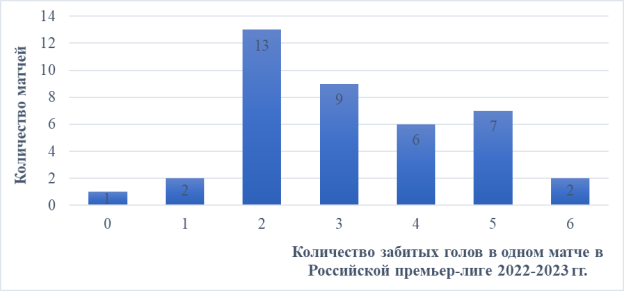
Рис. 2. Распределение «количества забитых голов в одном матче» на Российской премьер-лиге 2023–2024 гг.

5. Построив все таблицы, рассчитаем статистические характеристики.

Медиана ряда (определяем по табл. 2);

1. При n — четное (n — количество матчей, n = 40, i = 1: n)

Med = (x _t + x _{t +1} )/2, где t = n/2;

2. При n — нечетное.

Med = x _r , где r = (n+1)/2.

В данном примере медиана ряда равна 3.

Среднее значение ( определяем по табл. 2 ).

Sred = (x ₁ +x ₂ +…x _n )/n, где n — количество матчей, n = 40.

Мода ряда (определяем по табл. 3).

1. Находим максимальное значение количества матчей по формуле

y _m = max (y _j ) _,

где j — индекс варианта количества забитых голов в одном матче, j = 1:a, a — максимальное значение вариантов количества забитых голов.

2. Определяем величину моды по формуле

Mod = x _j

В данном примере a = 7, y _j = 13, j = 3, Mod = x _j = 2

Мода ряда = 2 (т. е. в 13 матчах турнира чаще всего забивали по 2 гола).

Размах ряда ( определяем по табл. 3).

₁₎ Raz = x _max — x _{min ,}

x _max = x _a = 6, где a — максимальное значение вариантов количества забитых голов, a = 7, j = 1:a.

x _min = x ₁ = 0

x _max = x _n = 6, где n — количество матчей, n = 40, i = 1: n.

x _min = x ₁ = 0

В данном примере размах ряда равен 6.

Итак, в результате проведенных расчетов можно сделать следующие выводы:

– медиана ряда, которая равна 3, указывает на то, что половина матчей в турнире имела количество забитых голов, не выше этого значения;

– среднее значение ряда, равное 3.15, показывает среднее количество забитых голов в матче;

– мода ряда, равная 2, указывает на то, что наиболее часто встречающееся количество забитых голов в одном матче — 2;

– размах ряда, равный 6, показывает разницу между наименьшим и наибольшим значением количества забитых голов.

Таким образом, по результатам анализа статистики футбольных матчей можно сделать вывод, что в течение 5 туров было достаточно большое разнообразие в количестве забитых голов, но самым часто встречающимся значением было 2 гола.

Рассчитав статистические показатели, тренеры команд могут принять наиболее верное решение повышения эффективности и результативности командной игры.

1. Российская премьер-лига по футболу [Электронный ресурс]: // URL: https://football.kulichki.net/ruschamp/2024/6/. (Дата обращения: 05.07.2023).