Парадокс двух конвертов

В статье описывается известная в теории вероятностных и статистических моделей задача о парадоксе двух конвертов, разрешение парадокса и дается ответ на вопрос: «Как сделать задачу корректной?».

Ключевые слова: парадокс двух конвертов, вероятность, моделирование, математическое ожидание.

Парадокс двух конвертов — это математический парадокс теории вероятностей. Предположим, в игре есть два закрытых конверта с деньгами. Один из них содержит в два раза больше денег, чем другой. Игрокам случайным образом раздают конверты, после чего у них есть возможность обменяться полученным. Игроки могут посмотреть содержимое своих конвертов, не сообщая другому свою сумму. Стоит ли игрокам меняться конвертами?

Предположим, игрок № 1 посмотрел, что его конверт содержит 100 рублей, тогда содержимое конверта игрока № 2 может составлять либо 50 рублей, либо 200 рублей. Поскольку из этих вариантов равновероятен, ожидаемое значение после обмена составляет

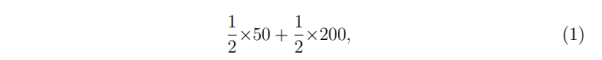
что равняется 125 рублям. Поскольку это больше, чем содержится в конверте игрока № 1, предполагается, что ему выгоднее будет поменяться. Это рассуждение работает для любой суммы, которая будет найдена в конверте. Так что неважно, посмотрел ли игрок в конверт или нет.

Но данное рассуждение работает как для игрока № 1, так и для игрока № 2, но выгодным для обоих быть не может. В этом и заключается парадокс.

Пусть A — величина суммы в конверте игрока № 1, а B — величина суммы в конверте игрока № 2. Предположим, что в конверте игрока № 1 сумма больше, чем у игрока № 2, тогда вероятность будет иметь вид

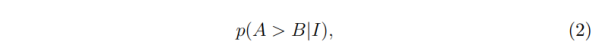
где I — это информация об игре, которая имеется до открытия конверта. Также (2) можно было бы записать как p(A = 2B|I), вероятность того, что A вдвое больше B.

Пусть f(x) — функция, такая, что f(s) — вероятность того, что в конверте с меньшим количеством денег находится s рублей.

Ожидаемое значение в конверте игрока № 2, если делать расчеты, опираясь на данные условия задачи, должно составлять

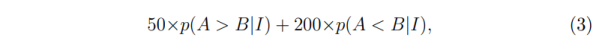
где

– p(A > B|I) — случай, когда конверт игрока № 1 имеет большую сумму;

– p(A < B|I) — случай, когда конверт игрока № 1 имеет меньшую сумму.

Каждая из этих двух вероятностей равна 1/2, что дает ожидаемое значение — 125 рублей. Но это на самом деле неверно. Количество рублей, умноженные на эти вероятности, используют информацию о том, что игрок № 1 знает, что в его конверте 100 рублей, и логично предположить, что вероятности также будут принимать во внимание эту информацию. Таким образом, правильный расчет:

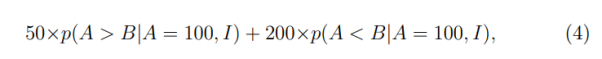
с появлением условных вероятностей. Первая вероятность — вероятность того, что игрок № 1 имеет большую сумму, учитывая, что сумма в конверте составляет 100 рублей — должно быть пропорционально вероятности того, что меньшая сумма — 50 рублей, которая была обозначена как f(50). Вторая вероятность — вероятность того, у игрока № 1 меньшая сумма, учитывая, что сумма конверта составляет 100 рублей — она должна быть пропорциональна f(100). Поскольку предоставленные два варианта — единственные (у игрока № 1 либо большая, либо меньшая сумма), сумма вероятностей должна быть равна единице. Чтобы гарантировать это, необходимо разделить оба значения f на их сумму:

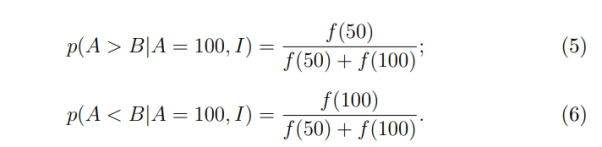
Можно увидеть, что эти две вероятности имеют правильную пропорциональность и в сумме равны единице. Если вместо 100 рублей в конверте игрока № 1 оказывается другая сумма, x, то ожидаемую сумму в другом конверте можно посчитать как

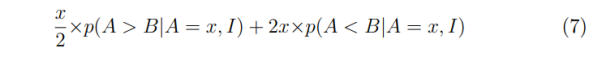
с вероятностями

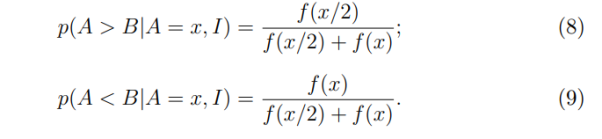
Теперь, когда выведена правильная формула для ожидаемого значения в другом конверте, необходимо сравнить это с предполагаемым изначально решением. Чтобы получить равные значения вероятностей 1/2, числители уравнений (9) и (10) должны равняться друг другу (так как знаменатели одинаковы). Итак, имеем

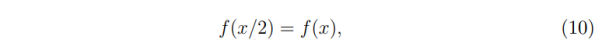
то есть вероятность того, что меньшая сумма равна тому, что находится в конверте игрока № 1 (x), и вероятность того, что меньшая сумма равна половине того, что находится в конверте игрока № 1 (x / 2), должны равняться друг другу.

Если возможные суммы в конвертах неограниченны, то f(x) никогда не обратится в ноль. Единственный случай, когда это может быть правдой — это если f(x) = f(x/2) для бесконечного числа значений x. Для этого f(s) должно быть равно некоторой константе C. Но так как 3 в этом случае должен быть бесконечный возможный выигрыш, сумма всех значений f(s) будет бесконечной для любого C кроме C = 0. Так что не может быть никакой игры, подходящей для условия постановки задачи, даже допуская возможность бесконечного выигрыша. Дело в том, что сумма вероятностей должна быть равна единице. Самый простой (и наиболее реалистичный) способ гарантировать это — наличие максимально возможного s. Когда это условие выполняется, нет никакого парадокса.

Представим игру, в которой сумму в конверте (любом) определяет распределение. То есть суммы в двух конвертах — независимые случайные величины с одним распределением.

Распределим суммы в конвертах на основе экспоненциального распределения. Математическое ожидание равно 1/λ, а медиана — ln(2)/λ.

По результатам моделирования видно, что выгоднее брать за пороговое значение математическое ожидание, и данная стратегия будет выигрышной.

Литература:

1. Zabell S. Proceedings of the Third Valencia International Meeting (англ.) — Clarendon Press, Oxford, 1988. Стр. 233–236.