Ключевые слова: теория узлов, движения Рейдемейстера, пара Перко, инвариант
Теория узлов — одна из наиболее красивых областей математики. Прародителем ее является К. Ф. Гаусс, который дал формулу для вычисления числа оборотов одной замкнутой кривой в трехмерном евклидовом пространстве вокруг другой.
Узлом называется гладкая замкнутая несамопересекающаяся кривая в пространстве, которую можно представить диаграммой, т. е. гладкой кривой на плоскости, не имеющей других особых точек, кроме конечного числа простых двойных точек (там, где происходит трансверсальное самопересечение), и снабженную в каждой двойной точке одним битом дополнительной информации, указывающим, какая из двух ветвей в этой точке является проходом (т. е. лежит снизу), а какая — переходом (т. е. лежит сверху). [1]
Автором первой книги, посвященной целиком теории узлов, был К. Рейдемейстер (1932), который доказал следующую теорему: две диаграммы узлов задают один и тот же узел тогда и только тогда, когда от одной из них можно перейти к другой посредством плоских изотопий диаграммы и перестроек Рейдемейстера.
Напомним, что в теории узлов, движением (преобразованием) Рейдемейстера называют одно из трех локальных движений на диаграмме узла или зацепления. В 1927 году Д. Александер и Бриггс, а также независимо К. Рейдемейстер, показали, что две диаграммы, относящиеся к одному и тому же узлу, с точностью до плоской изотопии могут быть преобразованы одна в другую с помощью последовательного применения одного из трех движений Рейдемейстера.
Каждое движение действует в небольшой области диаграммы и бывает одного из трех типов (рис. 1):
Тип I. Скручивание и раскручивание в любом направлении.
Тип II. Перемещение одной петли целиком через другую.
Тип III. Перемещение нити целиком над или под пересечением.
Заметим, что другие части диаграммы не отображены на схеме движения, а также, что плоская изотопия может исказить рисунок. Нумерация типов движений соответствует числу нитей, вовлеченных в него, к примеру, движение типа II действует на двух нитях диаграммы.
Один из важных случаев, когда требуется движение Рейдемейстера — это определение инвариантов узлов. Инвариант определяют, как свойство диаграммы узла, которое не меняется при любых движениях Рейдемейстера. Множество важных инвариантов можно определить таким образом, включая полином Джонса.
Только движения типа I изменяют число закрученности узла или зацепления. Движение типа III — единственное, которое не изменяет число пересечений на диаграмме.
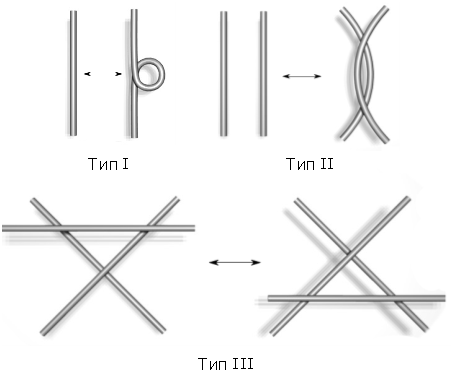
Рис. 1. Типы движений (преобразований) Рейдемейстера
Учитывая теорию особенностей (известную как теория катастроф) теорема Рейдемейстера вполне очевидна. Ясно, что любую гладкую изотопию узла в пространстве можно немного пошевелить так, что она сведется к последовательности элементарных перестроек указанных трех типов (преобразования Рейдемейстера). Однако актуальным является вопрос: каково минимальное число и какую последовательность перестроек Рейдемейстера необходимо совершить, чтобы преобразовать одну диаграмму узла в другую, если известно, что эти две диаграммы принадлежат одному классу эквивалентности.
Такова же задача актуальна и для кос. Существует множество алгоритмов, которые по двум математическим косам, записанным в образующих Артина, отвечают на вопрос, эквивалентны эти косы или нет (один из самых быстрых принадлежит И. А. Дынникову). Это стандартная постановка вопроса, которая известна, как проблема равенства (word problem) и может применяться не только к группе кос, но и к любой группе, заданной образующими и соотношениями.
Если в постановке задачи уже известно, что косы изотопны, то теоретически найти преобразование одной в другую минимальным числом движений Рейдемейстера можно простым перебором: для каждого 
перебирать все косы, которые получаются из первой косы применением 
движений Рейдемейстера, и проверять, нет ли среди них второй данной косы.
Такой перебор, конечно, будет огромен, так что этот подход дает только ответ на вопрос, можно ли найти минимальную последовательность движений Рейдемейстера. Теоретически — да, можно. Но вряд ли за разумное время.
За разумное время довольно просто решается другая задача — найти какую-то последовательность движений Рейдемейстера от одной косы к другой, но без претензий на то, что она будет кратчайшей. Из конструкции некоторых алгоритмов для решения проблемы равенства такая последовательность легко извлекается. Например, для этой цели подойдет алгоритм У. Тёрстона (W. Thurston) приведения к жадной нормальной форме (greedy normal form) или два алгоритма П. Деорнуа (P. Dehornoy) — сокращение ручек (handle reduction) и обращение слов (word reversing). Все эти алгоритмы достаточно быстрые, хотя для сокращения ручек хорошая оценка до сих пор не доказана.
Что касается узлов, то задача преобразования одного изотопного узла в другой решается намного сложнее. Чтобы оценить, насколько, достаточно ознакомиться с историей пары Перко (Perko pair): двумя эквивалентными друг другу узлами, которые в течение 75 лет, начиная с 1899 года, считались различными. Является очевидным, что быстрых алгоритмов, применимых на практике, для сравнения двух узлов на сегодняшний момент нет. Однако, существует достаточно надежный эфристический метод, реализованный в программе SnapPea Д. Викса (J. Weeks), которая умеет распознавать узлы с умеренным числом пересечений на диаграмме, но осуществляет это вне всякой связи с движениями Рейдемейстера. Однако, из процедуры, которую она выполняет, последовательность движений Рейдемейстера извлечь можно, но для этого программу придется усовершенствовать. Однако, для решения задачи вычисления минимальной последовательности преобразования одного изотопного узла в другой остается только снова полный перебор всех возможных вариантов.
Авторы благодарят доктора физ.-матем. наук, ведущего научного сотрудника МИАН И. А. Дынникова за полезные рекомендации и помощь в работе над статьей.
Литература:
- Дужин С. В., Чмутов С. В. Узлы и их инварианты // Математическое просвещение. — 1999. — № 3. — С. 59–93.
