Моделирование комбинаторных систем при помощи сводимости

Статья посвящена моделированию систем, ее реализации в компьютере, в частности с использованием сводимости, в то же время рассматривается теория алгоритмов и возможность ее применения к моделированию.

Ключевые слова: моделирование, комбинаторные системы, сводимость, учебный процесс, теория алгоритмов, теория систем

Под моделированием будем понимать реализацию функционирования объекта в компьютере. При этом целью обычно является оценивание средних величин. Методы моделирования изначально развивались для физики, в настоящее время трудно найти отрасль, где бы они не применялись. Можно также считать, что при моделировании рассматривают систему А, ее модель Б, а также вопрос, может ли Б служить адекватной моделью для А. В основании перехода часто лежит умозаключение по аналогии, которое дает вероятное знание [13].

Возьмем формальный язык L, основные символы которого будут интерпретированы так, чтобы на языке L удалось выразить отношения, согласно которым модель замещает объект. Можно считать L языком узкого исчисления предикатов, логические константы которого составляют сигнатуру . Через обозначим элементарную теорию объекта A, т. е. множество предложений, истинных в A [1]. Вообще нас могут интересовать не все свойства даже среди тех, которые выразимы на языке L. Поэтому естественно говорить о подмножестве В множества предложений языка L, выражающих интересующие исследователя свойства. Далее уточним форму отношения моделирования между объектами А и Б путем использования сведения проблемы истинности предложений для Б к проблеме истинности предложений из А.

В теории алгоритмов существуют различные классы сводимостей. Принципиально они отличаются по выбору одного или нескольких объектов для принятия решений, а также по тому факту, что информация может быть точно получена или может быть когда-либо получена, но в данный момент времени это неизвестно. Главное в процессе сведения — эффективность, или алгоритмичность.

Например, pm-сводимость (частичная) в применении выглядит следующим образом. Мы имеем возможность делать утверждения о свойствах Б на основании утверждений о свойствах А как конструктивное существование языка М и эффективного способа F перевода предложений P из В в предложения F(P) языка М таким образом, что

Важным здесь является не только эффективность F, но и невысокая алгоритмическая сложность F. Эта эквивалентность вообще говоря, может выполняться не на всех высказываниях, а на некоторой части, что соответствует неполному соответствию модели объекту.

Если построенная теория Т(Б) изучаемого объекта достаточно проста и допускает непосредственное изучение, тогда объектом А можно считать систему, для которой Т(А)=Т(Б) и тогда проблема адекватности модели — это проблема адекватности теории.

Если заданы теории объектов А и Б, то существование или несуществование сводимости является математической проблемой, решение которой в положительном смысле обосновывает отношение моделирования объектом А объекта Б в плане свойств из В, обосновывает с той достоверностью, с которой заданные теории адекватны своим объектам.

В математической логике одной из основных проблем является массовая проблема разрешимости для формальных теорий, т. е. проблема существования алгоритма, позволяющего по любому предложению языка определить, является ли оно истинным или принадлежит ли оно теории. Работы 30-х годов двадцатого века показали, что не существует разрешающего алгоритма для УИП, с тех пор было доказано много теорем об алгоритмической неразрешимости, причем большинство — путем сведения известной проблемы к рассматриваемой. Метод сводимости стал широко распространенным. Это и привело к изучению сводимостей как таковых. Сводимости стали мощным средством классификации множеств по сложности (степеням неразрешимости). Хорошим введением в эту область служит книга [3].

Введем необходимые формализмы. Множества и функции заданы на . Всюду определенные функции обозначаются через f,g,h, частичные — ,. — каноническая нумерация конечных множеств, — стандартная нумерация вычислимо перечислительных множеств (области определения частичных функций, задаваемых машиной Тьюринга с номером х). Среди сводимостей по разрешимости выделяютс наиболее общая тьюрингова и так называемые табличные сводимости. Говорят, что А tt-сводится к В, если существует алгоритм, который по любому дает набор чисел и -местную булеву функцию , зависящие от х такие, что

Сводимости, промежуточные по силе между m-сводимостью и tt-сводимостью, называются табличными или сходимостями табличного типа. Имеется естественный путь получения таких сводимостей. Для этого надо зафиксировать замкнутый класс булевых функций и в определении tt-сводимости добавить слова функция из такого-то класса. Оказалось, что основных табличных сводимостей существует всего лишь семь: кроме m- и tt-, еще линейная, конъюнктивная, дизъюнктивная, позитивная и табличная с нормой 1 [4,11]. Поскольку класс оказался четко очерчен, удалось поставить и решить вопросы о различии элементарных теорий, классов вычислимо перечислимых полных множеств [1,2].

Сводимости по перечислимости отличаются от сводимостей по разрешимости тем, что информацию про множество А рано или поздно можно будет получить, но про не обязательно. Говорят, что множество А е-сводится к В, если существует е-оператор Ф такой, что А=Ф(В). При этом е-оператор Ф переводит множество Х в

[2, 3, 5]

Сводимости, промежуточные по силе между е- и m-, образуют класс сводимостей по перечислимости. Основными сводимостями по перечислимости являются . В связи с тем, что вычислимо перечислимые множества образуют наименьшую e-степень, вопрос о полных множествах не стоит, зато с элементарными теориями удалось разобраться — они все попарно различаются [6–10].

Как уже отмечено, если и имеется способ перечислять B, то по нему можно получить и эффективное перечисление А. Это позволяет, например, по множеству свойств В моделирующей системы перечислять свойства из А моделируемой системы, если для множеств этих свойств установлено е-сведение. Но если на самом деле , то перечисляя А, мы просто не получим элемент , и вообще ни в какой момент времени нет оснований полагать, что . Этим отличаются сводимости по перечислимости.

Приведем пример.

Рассмотрим модель рюкзак. У нее входом X является пятерка . Здесь — некоторое конечное множество, — функции, отображающие в положительные целые числа , выход . Система функционирует посредством функции

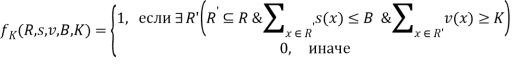
Система разбиение характеризуется входами , где — конечное множество, функция , выход . Система функционирует посредством функции

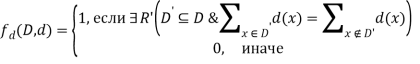
Основаниями для моделирования является алгоритмически построенное сведение множество истинных предложений одной системы к другой. В основном изучают входы и выходы одной системы, соответствующие входам и выходам другой.

Рассмотрим процесс моделирования системы разбиение системой рюкзак. Определим . Тогда можно заметить, что

Ясно, что данное соотношение выражает m-сводимость системы разбиение к системе рюкзак. [12]

Построим обратное сведение, т. е. промоделируем систему рюкзак системой разбиение. Введем еще одну функцию

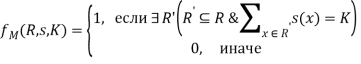
Тогда

, ,

,

Таким образом, система рюкзакd-сводится к системе разбиение и в целом эти две системы таблично или даже более точно, дизъюнктивно эквивалентны.

Рассмотрим пример из области принятия решений о законах распределения. Пусть f — закон распределения вещественной случайной величины, , Y — семейство всех конечных наборов вещественных чисел, — заданный уровень вероятности, и тогда и только тогда, когда — с вероятностью, большей α является набором значений случайной величины, распределенной по закону f. Пусть -нормальный закон распределения случайной величины с математическим ожиданием m и среднеквадратическим отклонением , - распределение Стьюдента с степенями свободы. Тогда

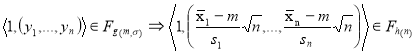, где

Здесь уже используется сводимость по перечислимости.

Таким образом, хотя понятия теории алгоритмов кажутся далекими от теории систем, они могут эффективно применяться при моделировании систем, в частности, при уточнении сложности систем, одной относительно другой, что позволит успешно ранжировать системы от простых к сложным или доказывать их эквивалентность.

Литература:

1. Дёгтев А. Н.. Рекурсивно перечислимые множества и сводимости табличного типа. — М.: Наука. Физматлит, 1998. -176с.
2. Дёгтев А. Н.. Избранные результаты по теории алгоритмов. Монография. Часть I. — Тюмень. Издательство ТюмГУ. 2008. 184с.
3. Соар.Р. И. Вычислимо перечислимые множества и степени: Пер. с англ. — Казань: Казанское математическое общество, 2000. — 576с.
4. Булитко В. К. Сводимости линейными по Жегалкину таблицами // Сиб.мат. журнал. 1980, Т.21, № 3. С.23–31.
5. Захаров С. Д. Об алгебре операторов перечисления // Вестник МГУ, сер. мат., мех., 1982, No 5, C. 79–83.
6. Захаров С. Д. О е- и s-степенях // Алгебра и логика, 1984. Т.23, No 4. С.395–406.
7. Захаров С. Д. О степенях сводимостей по перечислимости // Алгебра и логика. 1986. Т.25, № 2. С.121–135.
8. Захаров С. Д. Степени сводимостей по перечислимости (автореф. канд. дисс.)// Новосибирск, НГУ, 1986. — 14с.
9. Захаров С. Д. Степени сводимостей по перечислимости (диссертация) // Новосибирск, НГУ, 1986. — 75с.
10. Захаров С. Д. Об s-степенях внутри произвольной e-степени // Депон. В ВИНИТИ 20.01.90 № 740-С. — 18с.
11. Селиванов В. Л. Об одном классе сводимостей в теории рекурсивных функций // Вероятностные методы и кибернетика. Казань: Изд-во КГУ. 1982. Т.18 С.83–100.
12. Карп Р. М.. Сводимость комбинаторных задач. — Киб.сб. Н.С., 1975, вып. 12, С.16–38.
13. Казиев В. М. Введение в анализ, синтез и моделирование систем. Серия основы информационных технологий. Изд-во Интернет- Университет Информационных технологий, 2006.