В статье автор рассказывает о том, как можно использовать машинное обучение при создании информационной системы.

Ключевые слова: машинное обучение, нейронные сети, алгоритмы нейронных сетей.

Машинное обучение — это процесс обучения компьютерных систем на основе алгоритмов и статистических моделей, которые позволяют им учиться на основе предыдущего опыта и обрабатывать большие объемы данных. В контексте генеалогического древа математиков теории чисел машинное обучение может быть использовано для решения следующих задач:

1. Автоматическое заполнение данных: при создании генеалогического древа может возникнуть проблема нехватки информации о математиках, в том числе о их научных достижениях и учениках. В этом случае машинное обучение может использоваться для заполнения пропущенных данных на основе имеющихся сведений о математиках.
2. Выявление связей: Машинное обучение может помочь автоматически выявить связи между математиками и их учениками, которые могут быть упущены при ручной обработке данных.
3. Кластеризация: Машинное обучение может быть использовано для кластеризации математиков на основе их общих научных интересов, областей исследований и принадлежности к научным школам.
4. Предсказание научных достижений: Машинное обучение может использоваться для предсказания научных достижений учеников на основе данных об их учителях, их работах и научных интересах.
5. Оптимизация генеалогического древа: Машинное обучение может быть использовано для оптимизации структуры генеалогического древа, устранения дубликатов и корректировки ошибок в данных.

Рассмотрим более детально некоторые из вариантов и приведем примеры алгоритмов решающие данные задачи:

1. Классификация математиков по направлениям исследований: можно использовать алгоритмы классификации, например, Decision Tree или Random Forest, чтобы автоматически классифицировать математиков по их основным научным интересам. Для этого можно использовать данные из научных статей, которые они публиковали.
2. Поиск связей между математиками: можно использовать методы кластерного анализа, например, K-Means или DBSCAN, чтобы найти связи между математиками на основе схожести их научных интересов и совместных работ. Для этого можно использовать данные из научных статей и базы данных научных работ.
3. Прогнозирование будущих достижений математиков: можно использовать методы машинного обучения, например, регрессионный анализ или нейронные сети, чтобы прогнозировать будущие научные достижения математиков на основе их прошлых работ и научных интересов. Для этого можно использовать данные из базы данных научных работ и информацию о научной карьере каждого математика.

Рассмотрим примеры алгоритмов:

Random Forest:

Представим, что у нас есть база данных с информацией о математиках теории чисел и их учениках, включающая данные о публикациях, научных конференциях, диссертациях, а также списки учеников, их публикаций и диссертаций.

Мы можем использовать методы машинного обучения, такие как алгоритмы кластеризации или ассоциативные правила, чтобы анализировать эти данные и выявлять связи между математиками и их учениками.

Например, алгоритм кластеризации может группировать математиков и их учеников на основе схожих интересов и направлений исследований, что может указывать на наличие научных связей между ними.

(1)

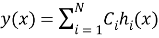
Где: — предсказанное значение,

— входные данные,

— решающее дерево,

— количество деревьев,

— коэффициент веса каждого дерева.

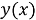
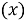
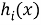
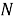
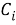
RNN:

Рекуррентная нейронная сеть (RNN) может быть использована для прогнозирования будущих научных достижений в рамках информационной системы генеалогического дерева математиков теории чисел.

Формула для построения такой сети может быть следующая:

(2)

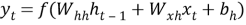
Где: — кол-во цитирований научной публикации в момент времени

— скрытое состояние на предыдущем временном шаге,

— входные данные на текущем временном шаге,

, , — параметры нейронной сети,

— функция активации, например, сигмоидная функция или функция ReLU.

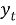
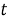
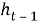
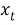
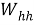
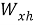
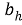
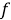
DBSCAN:

Метод кластеризации, который основывается на плотности точек в пространстве (DBSCAN). Он может быть использован для определения кластеров ученых, имеющих близкие связи друг с другом.

Алгоритм работы DBSCAN:

Пусть имеется множество точек в -мерном пространстве. Также есть параметры, задающие радиус и минимальное количество точек в кластере MinPts.

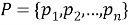
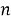
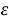
1. Находим все точки, которые находятся на расстоянии или менее от каждой другой точки. Эти точки образуют соседей каждой точки.
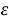
2. Если количество соседей точки больше или равно MinPts, то считается ядром кластера
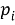
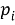
3. Для каждого ядра кластера находим все точки, которые достижимы от него (т. е. можно попасть в них, переходя только по точкам-соседям). Если количество таких точек больше или равно MinPts, то они также входят в кластер.
4. Если точки не являются ядрами кластеров и не достижимы из других точек, то они считаются выбросами.

Получается, что, множество точек разбивается на множество кластеров и множество выбросов . Каждый кластер является множеством точек, соответствующих ядру кластера, и всех достижимых из него точек, а множество выбросов содержит все точки, которые не являются ядрами кластеров и не достижимы из других точек.

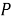
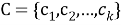
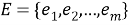
Вывод :

Таким образом, использование методов машинного обучения может помочь автоматически выявлять скрытые связи между математиками и их учениками и облегчить процесс построения генеалогического дерева. А также можно прогнозировать научные достижения.

Использование машинного обучения при разработки информационной системы генеалогического древа математиков теории чисел может существенно повысить эффективность и точность обработки данных и создать более полное и точное представление о научной деятельности и связях между математиками.

Литература:

1. Курпатов А. П. Машинное обучение: алгоритмы и приложения М.: ДМК Пресс, 2018.
2. Турчин В. Ф. Математические модели в машинном обучении М.: Физматлит, 2020.
3. Клейнер Г. А., Корнеев А. А. Генеалогические деревья и кластер-анализ. Информатика и ее применения, 2019, № 4, с. 23–29.
4. Буздин А. И. Машинное обучение. Теория и практика М.: ЭКСМО, 2021.
5. Мельников В. В. Применение алгоритмов машинного обучения в построении генеалогических деревьев математиков. Математическое моделирование и программирование, 2020, т. 11, № 3, с. 450–459.
6. Голубев А. Нейросети: Обучение на примерах. М.: Эксмо, 2020.
7. Штовба С. Д. Нейросети и обучение без учителя: основы теории и примеры практического применения М.: БИНОМ, 2019.