1.1. Треугольник и квадрат в геометрии Евклида.
Все мы в школе проходим геометрию, которую в III веке до нашей эры создал древнегреческий ученый Евклид. Безусловно, геометрия, как таковая, существовала и ранее, но именно Евклид изложил всю суть этой науки в своих трудах. Эта геометрия построена на системе аксиом, пяти постулатах и нулевой кривизне поверхности. Обычно ее называют евклидовой (элементарной) геометрией.
Все мы еще с младших классов знаем, что площадь квадрата в 2 раза больше площади треугольника, если их высоты равны. Либо треугольник и квадрат могут быть равны по площади, но тогда треугольник визуально будет выше или шире квадрата.
1.
2.
3.
Площадь треугольника номер 1 в два раза меньше площади квадрата, расположенного рядом. Но высота и длина основания треугольника равна длине каждой стороны квадрата. Площади треугольников и квадратов номер 2 и 3 равны. Но второй треугольник выше квадрата, а третий шире.
1.2. Что такое геометрии Лобачевского и Римана?
Вообще, неевклидовыми геометриями считаются все геометрии, отличные от евклидовой. В более узком смысле относится только к двум: Лобачевского (гиперболическая) и Римана (сферическая). Они основаны на отрицании пятого постулата Евклида о параллельных прямых.
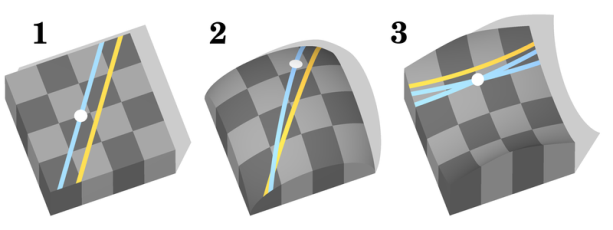
Под номером 1 представлена геометрия Евклида, под номером 2 — геометрия Римана и номер 3 — Лобачевского
В гиперболической геометрии через точку, не лежащую на данной прямой, проходят, как минимум, две прямые, параллельные данной. В сферической геометрии вообще не существует параллельных прямых. Любые прямые там обязательно пересекутся.
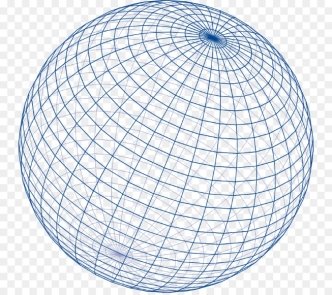
Ранее было упомянуто, что геометрия Евклида построена на нулевой кривизне поверхности. Геометрия Римана, в свою очередь, имеет положительною кривизну и строится на сферическом пространстве.
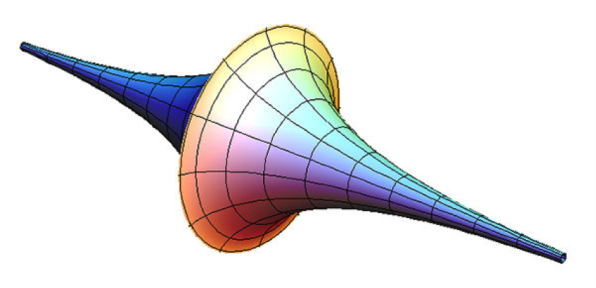
Геометрия Лобачевского имеет отрицательную кривизну и строится на псевдосфере.
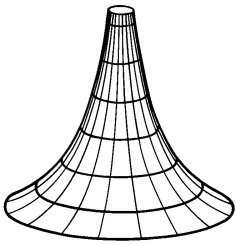
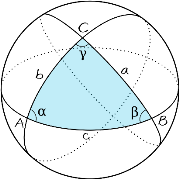
Также на основе данных утверждений известно, что сумма углов треугольника геометрии Лобачевского менее 180°, а геометрии Римана — более 180°. Четкая градусная мера суммы углов треугольника не определена, может быть любой.
1.3. Цель, задача и актуальность проекта.
В этом проекте я хотела доказать, что существуют такие треугольник и квадрат, площади которых будут равны и, также, высота и длина основания треугольника будут равны длинам сторон квадрата. Возможно это только в неевклидовых геометриях, если в сравнение брать треугольник из геометрии Римана и квадрат из геометрии Лобачевского, ведь гиперболический квадрат по площади меньше евклидового, а сферический треугольник — больше.
Цель: найти пропорции треугольника и квадрата, при которых высота и длина основания треугольника будут равны длинам сторон квадрата.
Задача: доказать равенство сторон фигур при заданных пропорциях.
Актуальность: неевклидовы геометрии находят свое применение в космосе. Геометрия Лобачевского используется в астрономии: при описании Вселенной или черных дыр. Плоскость Лобачевского — это космическое пространство, плоскость Римана — плоскость планет и других космических тел. Мой проект показывает, что фигуры в разных плоскостях могут быть равны.
2. Доказательство равенства фигур.
2.1. Равенство площадей.
В неевклидовых геометриях не существует подобных фигур. Но есть равные.
Напомним, подобными называются фигуры, одна из которых является уменьшенной моделью другой, а равными те фигуры, у которых равны стороны и углы.
Плоскость имеет радиус, то есть существует отрезок, соединяющий центр плоскости (сферы или псевдосферы) с любой точкой, лежащей на этой плоскости, а также существует длина этого отрезка. При увеличении длин сторон в геометрии Римана увеличивается сумма углов, приближаясь к 360°. В геометрии Лобачевского, наоборот, уменьшается, приближаясь к 0°. Минимальная сумма углов треугольника в геометрии Римана и максимальная в геометрии Лобачевского — это сумма углов евклидового треугольника. Площадь фигур напрямую зависит от суммы углов и радиуса плоскости, потому что при определенном радиусе и сумме углов существует только фигура с определенной площадью и длинами сторон.
Формула площади треугольника в геометрии Лобачевского:
R 2 ×(π-α-β-γ),
или:
R 2 ×(π-(α+β+γ)).
Формула площади треугольника в геометрии Римана:
(α+β+γ-π) ×R 2 ,
где R — радиус сферы и псевдосферы, π (3,14…) — математическая константа, выражающая отношение длины окружности к длине ее диаметра, α, β, γ — углы. В π радианах содержится 180°. Углы следует также перевести в радианы, чтобы можно было умножать их на сантиметры. Радиан — это угол, соответствующий дуге, длина которой равна ее радиусу. Градусы переводятся в радианы по формуле:
x° = (x° ⋅ π)/180° радиан.
Свойство 1
|
Равны площади фигур будут только в том случае, если будет равен модуль разности между суммой углов фигур и числом π. Также радиус должен быть одинаков. |
Также это свойство можно представить в виде формулы. Выглядеть она будет так:
ǀСумма углов 1 — πǀ × R = ǀСумма углов 2 — πǀ × R
Например, возьмем треугольник из геометрии Римана с суммой углов 200°, расположенный на сфере с радиусом 5 см. Найдем его площадь:
(200°-180°)×5=20°×5,
переведем 20° в радианы:
(20°×π)/180°=0,35 радиан.
Продолжим вычисление площади:
0,35×5=1,75.
Далее найдем площадь квадрата геометрии Лобачевского с суммой углов 160°, расположенный на псевдосфере с тем же радиусом, что плоскость треугольника:
5×(180°-160°)=5×20°,
снова переведем 20° в радианы, получится 0,35 радиан.
5×0,35=1,75.
1,75=1,75,
Соответственно площади разных фигур из разных геометрий могут быть равны.
2.2. Зависимость радиуса и сторон фигур.
Как было упомянуто ранее, подобных фигур в неевклидовых геометриях не существует. Из этого следует прямая зависимость радиуса, суммы углов и сторон фигуры. При изменении суммы углов, изменяются и стороны. Для того, чтобы приступить к этапу черчения треугольника и квадрата, нужно выявить зависимость длин сторон фигур от радиуса.
Если мы знаем, что сумма углов квадрата геометрии Лобачевского менее 360°, но более 0°, то у квадрата, площадь которого равно ¼ площади поверхности псевдосферы, сумма углов будет равна 180°, а стороны равны половине длины окружности. Из таких рассуждений делаем вывод, что
Свойство 2
|
Сторона квадрата геометрии Лобачевского равна тому же отношению к половине длины окружности, которому равна сумма его углов к 360°. |
Такую же зависимость имеют и равносторонние треугольники геометрии Римана, но неравносторонние следует строить на плоскости, для них это свойство не подойдет
2.3. Построение.
Сейчас мы приступим к самому главному этапу проекта — построение равных фигур. Для начала следует построить квадрат. Сумма углов нашего квадрата — 160°. Так как углы квадрата равны, каждый угол равен 40°. Напомню, радиус псевдосферы равен 5 см. Формула нахождения длины окружности:
P=2πR,
находим длину окружности:
2×π×5=31,4.
Из этого следует, что половина длины окружности равна 15,7.
Далее составим пропорцию и по свойству 2 находим длины сторон квадрата:
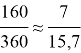
Чертим гиперболический квадрат, градусная мера углов которого равна 40°, стороны примерно равны 7 см.
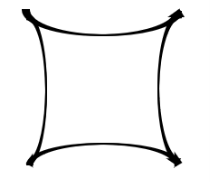
Выглядеть этот квадрат будет примерно так.
Также важно упомянуть, что угол в этих геометриях измеряется также, как и угол параболы, то есть угол между касательными этой параболы.
Далее мы построим треугольник, основание которого равно стороне квадрата, то есть 7 см. Для того, чтобы создать верное расстояние между точками и верную градусную меру дуги, следует измерить также расстояние между вершинами этого квадрата на евклидовой плоскости. Выглядеть это будет так:

Далее нужно отмерить высоту треугольника. Высота будет равна стороне квадрата, то есть 7 см. Но во время построения треугольника на евклидовой плоскости, высота будет равна тому же расстоянию между вершинами квадрата на евклидовой плоскости, то есть выглядеть оно будет так:
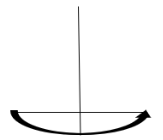
Далее нужно распределить 200° — сумму углов треугольника на три угла. Лучше это делать на макете сферы, также на сфере стоит проверять и длины двух сторон этого треугольника. Данный треугольник после всех измерений будет выглядеть так:
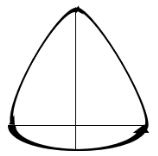
Снизу расположим квадрат:
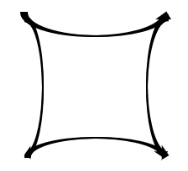
У нас получились равные треугольник и квадрат, с площадью 1.75 см., расположенные на сфере и псевдосфере 5 см.
3. Заключение.
Таким образом, в этом проекте мы доказали, что высота и основание треугольника и длины сторон квадрата, а также площади этих фигур могут быть равны в неевклидовых геометриях, что невозможно в геометрии Евклида. Также, мы вывели два довольно важных и интересных свойства, которые могут пригодиться в будущем.
Литература:
- https://ru.wikipedia.org/wiki/ %D0 %93 %D0 %B5 %D0 %BE %D0 %BC %D0 %B5 %D1 %82 %D1 %80 %D0 %B8 %D1 %8F_ %D0 %9B %D0 %BE %D0 %B1 %D0 %B0 %D1 %87 %D0 %B5 %D0 %B2 %D1 %81 %D0 %BA %D0 %BE %D0 %B3 %D0 %BE
- https://yandex.ru/video/preview/?text= %D0 %B3 %D0 %B5 %D0 %BE %D0 %BC %D0 %B5 %D1 %82 %D1 %80 %D0 %B8 %D1 %8F %20 %D0 %BB %D0 %BE %D0 %B1 %D0 %B0 %D1 %87 %D0 %B5 %D0 %B2 %D1 %81 %D0 %BA %D0 %BE %D0 %B3 %D0 %BE&path=wizard&parent-reqid=1616468222584933–642134348408164518300271-production-app-host-sas-web-yp-151&wiz_type=vital&filmId=10925938936116671307
- https://www.youtube.com/watch?v=ZlhdzGU9ySE

