- Введение
Несколько тысяч лет назад было изобретено колесо, которое произвело переворот в жизни человека. Определяющим свойством круга, лежащего в основе колеса, следствием которого стало техническое завоевание мира, стало свойство постоянства ширины. Существует мнение, что круг является единственной выпуклой фигурой, у которой ширина в любом направлении одна и та же и равна диаметру круга. А так ли это на самом деле? Существуют ли еще фигуры постоянной ширины? К множеству фигур постоянной ширины, кроме круга, относятся «круглые» n-угольники (где n — нечетное число), среди которых особенными «замечательными» свойствами обладает треугольник Рёло. Если внимательно присмотреться к окружающим нас предметам, то можно заметить, что многие из них имеют форму фигур равной ширины.
В современном мире развивающихся технологий невозможно обойти стороной фигуры постоянной ширины. Они занимают значительное место в науке и прикладной деятельности. Фигуры постоянной ширины позволяют сократить затраты в производстве, они используются не только в механике, но и в музыке, архитектуре
Актуальность :
В настоящее время очень остро стоит вопрос рационального использования ресурсов. Многие предприятия ставят себе задачу экономии сырья и материалов для оптимизации производства, сокращения себестоимости выпускаемой продукции, но сохраняя ее качественные характеристики.
Проблема :
Существует ли возможность сократить расходы при производстве круглых деталей?
Цель:
1. Выяснить, что представляют собой фигуры постоянной ширины.
2. Показать роль и значение этих фигур.
3. В доступной и занимательной форме заинтересовать учащихся моего лицея фигурами постоянной ширины.
Задачи:
1. Изучить литературу о фигурах постоянной ширины.
2. Исследовать главные свойства этих фигур.
3. Построить фигуры постоянной ширины и показать принципы их работы на самостоятельно изготовленных моделях.
Методы:
- Общенаучные: эксперимент, наблюдение, анализ.
- Работа с различными источниками информации (книги, сайты в сети Интернет).
- Систематизация и анализ данных.
- Наглядно-иллюстративный.
- Моделирование.
Область исследования: геометрия.
Объект исследования: фигуры постоянной ширины.
Предмет исследования : практическое применение свойств фигур постоянной ширины.
I. Теоретическая часть
1.1. История изучения фигур постоянной ширины
Фигуры постоянной ширины — это плоская выпуклая кривая, ограничивающую такую выпуклую фигуру на плоскости, для которой расстояние между каждой парой параллельных опорных прямых равно одному и тому же постоянному числу h.
Первооткрыватель этих фигур науке неизвестен. Но в XIII создатели церкви Богоматери в Брюгге (Бельгия) использовали треугольник Рёло в качестве формы для некоторых окон. В готической архитектуре постоянно встречаются элементы, образованные по принципу треугольника Рёло: стрельчатые арки, раскладка окон или оконные решетки на соборах и церквях, тимпаны — как ниши или как части фронтона (рис 1.).



Рис 1.
Искусствовед Дмитрий Антропов утверждает: «…Использование стрельчатой арки позволяет распределить массу не на всю стену, а на отдельные опоры». Таким образом, конструктивные особенности «круглого треугольника» позволяли сделать здание не только красивым, но и более безопасным.
В рукописях XV века великого Леонардо да Винчи мы встречаем треугольник Рёло (манускрипты A и B, хранящихся в Институте Франции, а также в Мадридском кодексе) (рис. 2).

Рис. 2
Тело постоянной ширины берёт своё начало с работ Леонарда Эйлера, который обнаружил треугольник Рёло, часто использующийся в английских готических церквях конца XIII века. Его работу завершил Дэн Бергеруд, заменив края тетраэдра группой сфер, соприкасающихся с краями, создав твёрдый объект с аналогичной симметрией и постоянной шириной.
Кстати, Франц Рёло́ (1829–1905), немецкий учёный, не являлся первооткрывателем этой фигуры. Он лишь нашёл практическое применение в кинематике. Но он внес наибольший вклад в изучение фигур постоянной ширины, их стали называть его именем (треугольник Рёло, пятиугольник Рёло и т. д.)
Изучение это носило большей частью практический характер и касалось применения фигур постоянной ширины в устройствах механизмов. Франц Рёло занимался проблемами эстетичность технических объектов, промышленным дизайном. В своих конструкциях придавал большое значение внешним формам машин, за что Рёло при жизни называли «поэтом в технике»
А вот австрийский геометр Вильгельм Бляшке изучал кривые постоянной ширины теоретически, как математик. В 1912 году дал, возможно, самое элегантное доказательство неизгибаемости замкнутых гладких выпуклых поверхностей. В книге «Круг и шар», вышедшей на немецком языке в1916 году, создал важный метод доказательства теорем о выпуклых телах. Ключевое утверждение, на котором базируется тот метод, сейчас называется теоремой выбора Бляшке.
1.2. Построение фигур постоянной ширины
Может показаться, что круг является единственной выпуклой фигурой, у которой ширина в любом направлении одна и таже: она равна диаметру круга. Однако это не так: существует множество фигур постоянной ширины, т.е таких выпуклых фигур, у которых во всех направлениях ширина одинакова.
Самая распространенная такая фигура, которую мы уже выше рассматривали, это треугольник Рёло. Но она не единственная. Существуют «круглые» пятиугольники, семиугольники… Вообще кривую постоянной ширины можно построить на любом нечетном многоугольнике (многоугольнике с нечетным количеством вершин). Почему именно нечетном? Многоугольник должен иметь нечетное число сторон потому, что у каждой вершины, которые соединяются дугой окружности радиуса h. (рис. 3)

Рис. 3.
Как же проводится построение. Есть два способа.
Построение с помощью циркуля .
Строим окружность заданного диаметра с произвольным центром. Центром второй окружности с тем же диаметром может быть любая точка первой окружности, а центром третьей — любая из двух точек пересечения первых двух окружностей. Построение «круглых» пятиугольника и семиугольника тоже возможно с помощью циркуля, только пересекаться будут не три, а пяти и семь кругов соответственно (рис. 4).
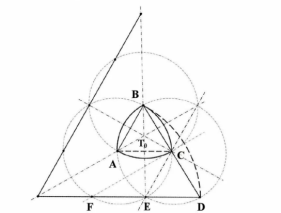
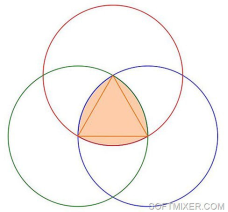
Рис. 4.
Построение с помощью циркуля и линейки .
Строим равносторонний (правильный) треугольник с помощью циркуля и линейки. Раствор циркуля берем равным длине стороны треугольника, центром выбираем одну из вершин, чертим дугу на противоположной стороне треугольника (рис. 5).
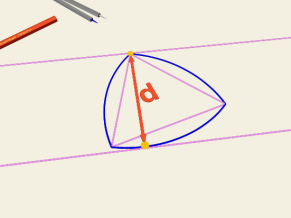
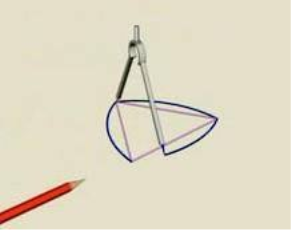
Рис. 5
Другие многоугольники Рёло строятся аналогично.
Существуют и неправильные многоугольники Рёло.
Можно построить и несимметричные фигуры постоянно ширины.
Также существуют и объемные фигуры постоянной ширины: тетраэдр Рёло например (рис. 6).


Рис. 6
- Свойства фигур постоянной ширины
( Теорема Барьбье ) Длина кривой постоянной ширины a равна πa.
Это основополагающий результат, установленный французским математиком Жозефом Луи Франсуа Барбье в 1860 году. Он утверждает, что длина любой кривой, обладающей постоянной шириной a, равна числу π, умноженному на саму ширину a. Таким образом, длина такой фигуры никак не зависит от ее конкретной формы, а определяется лишь ее шириной.
Центры вписанной и описанной окружностей в кривую постоянной ширины совпадают, а сумма их радиусов равна ширине кривой.
Это важное геометрическое свойство фигур постоянной ширины. Оно означает, что центр вписанной в такую фигуру окружности и центр описанной вокруг нее окружности совпадают. При этом сумма радиусов этих двух окружностей всегда равна ширине самой фигуры.
Фигура постоянной ширины a может вращаться в квадрате со стороной a всё время касаясь каждой из сторон.
Еще одно интересное свойство — фигура постоянной ширины a может совершать вращение внутри квадрата со стороной, равной ее ширине a , при этом обязательно касаясь каждой из сторон квадрата. Это наглядно демонстрирует постоянство ширины такой фигуры.
Среди фигур постоянной ширины a треугольник Рёло имеет наименьшую площадь, а круг — наибольшую.
Среди всех возможных фигур постоянной ширины a треугольник Рёло имеет минимальную площадь. В то же время круг, обладающий постоянной шириной, имеет максимальную площадь по сравнению с другими фигурами той же ширины. Это интересное сравнение различных фигур постоянной ширины.
- Применение фигур постоянной ширины в жизни
Первый пример : Вы опускаете монету в автомат, и она отправляется в путь по монетоприёмнику. Чтобы монета не застряла, можно, конечно, расширить трубку металлоприёмника. А можно изготавливать монеты в виде фигур постоянной ширины, тогда они не застрянут в трубке, даже вращаясь. Простейшая фигура постоянной ширины, как мы знаем, — круг, в форме которого делают большинство монет. Но есть и исключения. В Великобритании 20- и 50-пенсовые монеты имеют форму фигуры постоянной ширины, построенной на правильном семиугольнике. Такая же форма у монет достоинством в полдинара, находящихся в обращении в Иордании. Изготовление монет в виде фигур постоянной ширины, отличных от круга, позволяет экономить металл, ведь, как мы знаем, при фиксированной ширине круглая монета — самая металлоёмкая.
Монета Великобритании пятьдесят пенсов изготовлена в форме семиугольника Рёло. Её диаметр равен 27,3 мм, масс 8 г, толщина 1,78 мм, а изготовлена из сплава меди и никеля (75 ° Cu, 25 ° Ni). Достаточное количество меди и никеля удалось сэкономить англичанам на производстве скруглённых монет, если на декабрь 2005 года в обращении находилось 769 миллионов 50-центовых монет (рис. 7).

Рис. 7
Второй пример. До наступления цифровой эпохи, когда фильмы снимались и демонстрировались на киноплёнке, в кинокамерах и кинопроекторах использовались специальные механизмы для её перемещения. Этот механизм назывался грейферным и обеспечивал скачкообразное движение плёнки вдоль объектива с определённой частотой — стандартно 18 скачков в секунду.
Ключевым элементом, который управлял работой грейферного механизма, был треугольник Рёло. Это было устройство, состоящее из трёх зубчатых колёс, расположенных в форме треугольника. Вращение этого треугольника задавало точный ритм, с которым происходило прерывистое движение киноплёнки в камере и проекторе.
Таким образом, треугольник Рёло играл важную роль в обеспечении стабильной и синхронизированной работы механизмов киносъёмки и кинопоказа в доцифровую эпоху, когда фильмы создавались и демонстрировались исключительно на киноплёнке с помощью аналоговой техники (рис. 8).
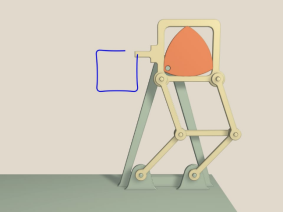
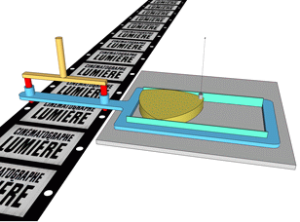
Рис. 8
Третий пример . Из области автомобилестроения. В конце 1940-х годов Ф. Г. Ванкель придумал схему двигателя без коленчатого вала, в котором поступательное движение поршней преобразуется во вращение вала мотора. В этом двигателе, называемом роторным, нет цилиндров. Ротор при вращении постоянно касается стенок камеры двигателя, разделяя рабочее пространство на три части. В двигателе Ванкеля форма ротора в сечении — треугольник Рёло (рис. 9).

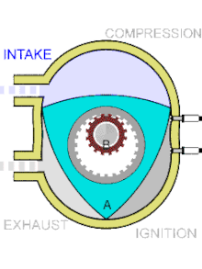
Рис. 9
Четвертый пример. «Сверло Уаттса». Идея этого сверла основана на свойствах движения треугольника Рёло. Как было отмечено ранее, если центр треугольника Рёло двигается по замкнутой кривой, а сам треугольник вращается вокруг этого центра, то он «захватывает” область, имеющую форму квадрата с закругленными углами.
Инженер Джеймс Уатт применил этот принцип при конструировании специального сверла. Вместо стандартного круглого сверла, он создал сверло, которое позволяет получать почти квадратные отверстия.
Принцип работы «сверла Уаттса» заключается в следующем:
Центр сверла движется по круговой траектории, описывая окружность.
При этом само сверло вращается вокруг своего центра, подобно движению треугольника Рёло.
В результате такого комбинированного движения, сверло срезает материал по четырем сторонам, формируя почти квадратное отверстие.
Таким образом, использование идеи движения треугольника Рёло позволило Джеймсу Уатту создать уникальное сверло, которое может формировать отверстия с формой, близкой к квадратной. Это стало ценным инженерным решением, позволяющим получать нестандартные отверстия там, где это необходимо (рис. 10).

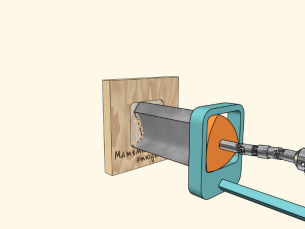
Рис. 10

Рис. 11. Крышка люка в Сан-Франциско
Пятый пример . Крышки люков, спасающие пешеходов от падений в колодцы и мешающие автомобилистам, чаще всего круглые. Выбор такой формы объясняется соображениями безопасности: квадратная крышка при сдвиге может провалиться в люк, поскольку сторона квадрата меньше его диагонали. А у круга есть замечательное свойство — эта фигура постоянной ширины. Но для экономии металла, иногда делают крышки люка в форме фигур постоянной ширины (рис. 11).
Шестой пример. Форма фигур постоянной ширины, в частности треугольника Рёло, используется в формах разных мелких бытовых предметов, мебели и архитектурных планировках (рис. 12).
— Цикля для снятия краски

Рис. 12
— Треугольник Рёло — распространенная форма плектра (медиатора), тонкой пластинки, предназначенной для игры на струнах щипковых музыкальных инструментов (рис. 13).


Рис. 13
— Сечение башни делового центра «Кёльнский треугольник» в Кёльне выполнено в форме треугольника Рёло (рис. 14).

Рис. 14
— Музей компании Mercedes-Benz в Штутгарте выполнен в форме «круглого треугольника» Рёло (рис. 15)

Рис. 15
— Современные студенты-архитекторы тоже любят экспериментировать с формой треугольника Рёло, создавая красивые современные здания (рис. 16).
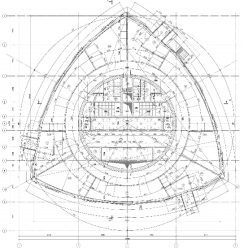
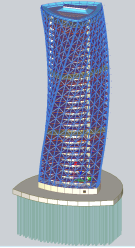
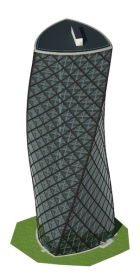
Рис. 16
—Архитектор и дизайнер Максим Казанский: «Благодаря кривой Рёло здания получают футуристичные очертания. Есть в ней что-то инопланетное, близкое к НЛО. Мне, как дизайнеру, этот треугольник очень близок» (рис. 17).


Рис. 17
— Очень интересное применение фигур постоянной ширины в спирографе. Интересно будет и детям, и взрослым создавать графические шедевры.
Спирограф способствует развитию координации движения кисти, моторики руки. Формирует способность к рисованию (рис. 18).


Рис. 18
В научной фантастике авторы также используют удивительные свойства треугольника Рёло. Так в рассказе Пола Андерсона «Треугольное колесо» экипаж землян совершил аварийную посадку на планете, население которой не использовало круглые колеса, так как всё круглое находилось под религиозным запретом. В сотнях километров от места посадки предыдущая земная экспедиция оставила склад с запасными частями, но перенести оттуда необходимый для корабля двухтонный атомный генератор без каких-либо механизмов было невозможно. В итоге землянам удалось соблюсти табу и перевезти генератор, используя катки с сечением в виде треугольника Рёло.
— Форма фигур постоянной ширины не дает покоя современным изобретателям. Велосипед с треугольными колесами. Изобретение создал инженер Сергей Гордиев. Для этого он взял образец транспорта, представленный во время мероприятия Burning Man в 2012 году.
Идея Сергея Гордиева следующая: «Почему бы не использовать этот принцип для колёс? Ведь треугольник Рёло является самой известной кривой постоянной ширины, которая не является кругом, в отличие от обычных шин».
Таким образом, был создан необычный велосипед, который движется намного плавнее, чем это можно представить. В том числе благодаря двойному амортизатору, способному сглаживать удары на поворотах. Подобный вид транспорта не будет самым удобным в использовании, однако он точно привлечёт к себе внимание на улицах города (рис. 19).

Рис. 19
II. Практическая часть
2.1. Модель движущейся платформы с колесами с сечением формы треугольника Рёло
Экспериментальное исследование движения тел, перемещаемых с помощью фигур равной ширины
Наши предки использовали круглые брёвна одинакового диаметра для перемещения огромных камней, массивных скульптур, на которые ставили плоскую платформу с грузом. Такой способ возможен потому, что круг — фигура равной ширины. Выше доказано, что к семейству фигур равной ширины относится и треугольник Рёло, а значит, он также может быть использован для перемещения тел.
Для проверки этого предположения нами был проведен следующий эксперимент. В качестве катков, имеющих в поперечном сечении треугольник Рёло, были выбраны карандаши. В качестве платформы использована крышка от коробки, а в качестве груза и одновременно индикатора — стакан с колой. При прокатывании крышки, имеющей форму фигуры равной ширины, по ряду карандашей-катков, уровень жидкости (например, колы) в стакане, установленном на крышке, остается постоянным. Это наглядно демонстрирует, что перемещаемое тело (крышка) движется строго прямолинейно, несмотря на кругообразное движение катков.
Такое поведение фигур равной ширины объясняется их геометрическими свойствами — они могут перекатываться, сохраняя постоянное расстояние от плоскости качения. Таким образом, жидкость в стакане сохраняет свой уровень, так как центр тяжести крышки движется по прямолинейной траектории (рис. 20).

Рис. 20
Данный эксперимент наглядно иллюстрирует практическое применение фигур равной ширины, в частности, их использование в различных механизмах для обеспечения прямолинейного перемещения. Это свойство находит применение в конструкциях, где требуется стабильность положения объектов при движении.
Вывод. Поскольку сечение роликовых опор имеет форму фигуры равной ширины, плоская платформа, опирающаяся на эти ролики, перемещается прямолинейно и сохраняет параллельность плоскости, по которой происходит качение.
Изготовление модели. Данную модель мы делали из подручных и доступных материалов, чтобы наглядно показать, что фигуры постоянной ширины присутствуют в нашей жизни в различных интерпретациях.
2.2. Модель люка-сортера с фигурами постоянной ширины
Вторым экспериментом мы хотели бы представить демонстрационную модель люков формы фигур постоянной величины. Для сравнения представлен квадратный и треугольный люки, которые провалятся в свои же отверстия, если их повернуть наискосок (рис. 21).

Рис. 21
Изготовление модели. Две пластины с отверстиями и вкладыши были изготовлены из экологичного материала (натурального дерева) с помощью лазерной резки. Заготавливались две пластины. В одной из них вырезались отверстия для фигур на 2 мм по периметру меньше, чем в другой. Затем обе пластины склеивались в один блок. Использовался не токсичный клей на водной основе. В результате фигуры, уложенные в отверстия первой пластины не должны проваливаться насквозь. Сами фигуры выкрашены в разные цвета акриловыми красками.
2.3. Модель «качание по квадрату»
Третьим экспериментом, мы хотели бы представить дидактическое пособие в виде большого треугольника Рёло в замкнутом квадрате. Описанный эксперимент демонстрирует интересное свойство фигуры равной ширины — большого треугольника Рёло, вписанного в квадрат. При вращении этой конфигурации, края треугольника будут очерчивать слегка закругленный квадрат, подобно сверлу Уоттса.
Это еще одно проявление особенностей фигур равной ширины — их способности двигаться прямолинейно, сохраняя параллельность плоскости качения. Этот эффект находит применение в различных механизмах и устройствах, где требуется прямолинейное перемещение платформ или деталей (рис. 22).

Рис. 22
Изготовление модели. Для изготовления данной модели, мы взяли лист тонкой фанеры и вырезали квадрат размером 25х25 см с помощью лазерной резки. Затем изготовили из такого же материала квадратную рамку с габаритами 25х25 см и толщиной рамки 2,1 см. Склеили клеем на водной основе квадратное основание и рамку. Затем из фанеры вырезали фигуру треугольника Рёло (предварительно начертив шаблон по расчетам). R окружности = ширина треугольника. Чтобы удобно было продемонстрировать вращение треугольника в рамке, мы прикрепили ручку-кнопку (рис. 23).
Рис. 23
III. Заключение
Подведем итоги проделанной работы
1. Мы представили 3 дидактических пособия, наглядно демонстрирующие лицеистам и гостям нашего лицея ознакомиться с фигурами постоянной ширины, их свойствами и их практическим применением:
— Эксперимент с прокатыванием крышки по карандашам-каткам, демонстрирующий прямолинейное движение фигур равной ширины
— Другие примеры использования фигур постоянной ширины в различных механизмах
2. Мы отметили, что отличительные свойства треугольника Рёло находят множество практических применений. Использование их вместо круга позволяет экономить материал и облегчать инженерные конструкции. Это показывает, что более глубокое изучение фигур постоянной ширины может раскрыть еще больше областей их использования.
3. Таким образом, наша работа показывает важность и перспективность исследования свойств фигур постоянной ширины, а представленные наглядные модели могут стать ценным инструментом для популяризации и вовлечения обучающихся в изучение этой интересной математической темы.
Надеемся, что наш подход к раскрытию практического применения математических объектов является ценным и поможет повысить мотивацию учеников к изучению математики.
Литература:
- Борисенко, А. И. Геометрические построения с помощью циркуля и линейки / А. И. Борисенко. — К.: Вища школа, 1990. — Глава 7: Фигуры постоянной ширины.
- Кузнецов, О.П., Сосин, А. Б. Конструкции с фигурами постоянной ширины // Техническая эстетика. — 1979. — № 11. — С. 20–22.
- Олехник, С.Н. Старинные занимательные задачи / С. Н. Олехник, Ю. В. Нестеренко, М. К. Потапов. — М.: Наука, 1985. — Глава 5: Фигуры постоянной ширины.
- Пол Андерсон. Треугольное колесо.
- Чехов, А. П. Фигуры постоянной ширины в технике / А. П. Чехов // Квант. — 1978. — № 7. — С. 10–15.
- Яглом, И. М. Фигуры постоянной ширины / И. М. Яглом. — М.: Наука, 1962. — 124 с.
- Gardner, M. Mathematical Games: The remarkable lore of the wheel of constant width / M. Gardner // Scientific American. — 1959. — Vol. 200, No. 5. — P. 188–200.
- Stakhov, A. P. The Mathematics of Harmony: From Euclid to Contemporary Mathematics and Computer Science / A. P. Stakhov. — Singapore: World Scientific Publishing, 2009. — Chapter 7: Curves of Constant Width.

