Объемные фигуры в неевклидовых геометриях



1. Введение

1.1. Что такое неевклидовы геометрии

Отцом геометрии считается ученый Евклид. Именно он в III веке до нашей эры изложил всю суть этой науки в своих трудах. Привычная нам геометрия построена на системе аксиом, пяти постулатах и нулевой кривизне поверхности. Обычно ее называют евклидовой (элементарной) геометрией.

Неевклидовы геометрии — это геометрии, отличные от евклидовой. К ним относятся геометрия Лобачевского (гиперболическая) и геометрия Римана (сферическая).

Гиперболическая геометрия имеет отрицательную кривизну поверхности и строится на псевдосфере, имеющей радиус.

Сферическая геометрия Римана строится на сфере и имеет положительную кривизну.

Вышеупомянутые геометрии были выведены после попытки Лобачевского доказать от противного пятый постулат Евклида о параллельных прямых. Эти геометрии строятся на отрицании данного постулата.

1.2. Теория для двухмерного пространства

Для начала я предлагаю рассмотреть геометрию Евклида.

Постулаты Евклида:

1. От любой точки до любой точки можно провести прямую.
2. Участок прямой можно непрерывно продолжать по прямой.
3. Из всякого центра и всяким раствором может быть описан круг.
4. Все прямые углы равны между собой.
5. Если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых углов (равных 90°), то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых углов.

Пятый постулат выглядит сложнее остальных. Многие ученые хотели доказать его, но впоследствии стало понятно, что он недоказуем и именно это привело к появлению неевклидовых геометрий, основанных на отрицании этого постулата.

Данный постулат связан с понятием о параллельных прямых. Именно это понятие отличает геометрию Евклида от сферической и гиперболической геометрий.

Рассмотрим параллельные прямые в разных геометриях:

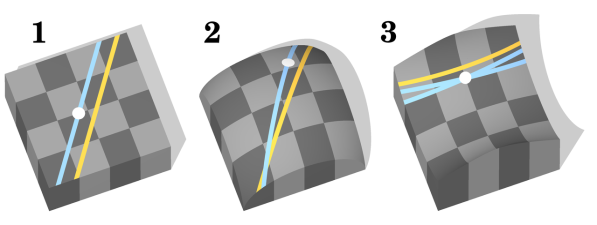
Рис. 1. Параллельные прямые в геометрии Евклида

В геометрии Римана, которая строится на сфере, параллельных прямых не существует. Любые прямые обязательно пересекутся (рис. 2).

В геометрии Лобачевского, которая строится на псевдосфере, две прямые могут пересекаться, но при этом быть параллельными третьей (рис. 3).

Напомню, что геометрия Лобачевского строится на псевдосфере, а геометрия Римана на сфере. Фигуры в этих геометриях выглядят не так, как на Евклидовой плоскости.

Как я упоминала ранее, у плоскости неевклидовых геометрий существует радиус. Из этого следует то, что плоскости имеют определенный размер и различные плоскости могут быть разных размеров. Главной характеристикой фигуры является сумма ее углов. Две одинаковые фигуры с одинаковыми углами, но находящиеся на плоскостях разных размеров, будут различны. Из вышесказанного делаем вывод, что подобных фигур, находящихся в одной плоскости, не существует. Существуют только равные.

В этом проекте, в основном, мы будем рассматривать треугольники и тетраэдры.

В сферической геометрии сумма углов треугольника более 180 градусов (рис. 2, слева), в гиперболической менее 180 (рис. 2, справа).

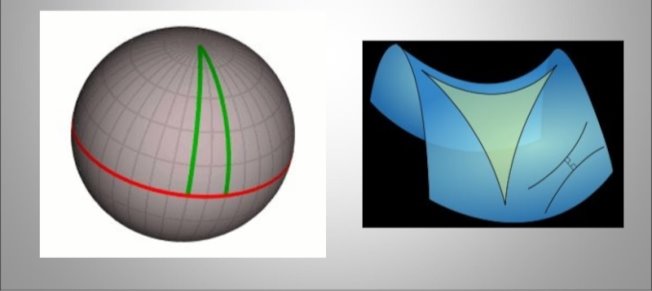
Рис. 2

1.3. Цели и задачи проекта

В этом проекте я хотела бы разобраться, могут ли в неевклидовых геометриях существовать объемные фигуры. Если будет доказано, что они существуют, вывести формулы для этих геометрий.

Цель проекта: разобраться, существуют ли объемные фигуры в геометриях Лобачевского и Римана.

Задачи:

1. Разобраться, существует ли пересечение плоскостей в этих геометриях.
2. Построить объемные фигуры на этих плоскостях.
3. Создать формулы для трехмерного пространства в геометрии Лобачевского и геометрии Римана.

Актуальность:

Неевклидовы геометрии используются в астрономии и астрофизики для описания Вселенной: темной материи, черных дыр. В основном, в астрономии геометрия Лобачевского представляется и используется как двухмерная.

Доказав, что в неевклидовых геометриях существует трехмерное пространство, можно будет предположить, что пространство во Вселенной четырехмерно.

2. Сравнение свойств неевклидовых геометрий и геометрии Евклида.

2.1. Теоремы и аксиомы планиметрии.

Неевклидовы геометрии отличаются от евклидовой только параллельными прямыми и тем, что связано с ними. Остальные аксиомы и теоремы работают для всех геометрий.

Предлагаю разобраться, в чем именно заключаются различия между этими геометриями.

Сумма углов треугольника

Самое первое различие, которое бросается в глаза — это теорема о сумме углов треугольника. В геометрии Евклида она равна 180°, в геометрии Лобачевского — менее 180°, а в геометрии Римана — более 180°.

Для того, чтобы объяснить это, сначала вспомним доказательство Евклидовой теоремы.

Пусть АВС — треугольник. Проведем через вершину В прямую, параллельную АС. На ней отметим точку D так, чтобы точки А и D лежали по разные стороны от прямой ВС. Углы DBC и АCB равны как внутренние накрест лежащие, образованные секущей ВС с параллельными прямыми АС и ВD. Поэтому сумма углов треугольника при вершинах В и С равна углу ABD. Сумма всех углов треугольника равна сумме углов ABD и BAC. Так как эти углы внутренние односторонние для параллельных АС и BD при секущей AB, то их сумма равна 180°.

Эта теорема зависит от параллельных прямых. В неевклидовых геометриях постулат о параллельных прямых не работает, поэтому и теорема о сумме углов треугольника тоже не может быть такой.

Подобие

Площади фигур в сферической и гиперболической геометриях зависят от углов и радиуса сферы и псевдосферы, на которых строятся эти фигуры. Представим формулу площади треугольника в геометрии Римана (1) и геометрии Лобачевского (2).

R ² ×(π-α-β-γ) (1)

(α+β+γ-π) ×R ² , (2)

где R — радиус сферы и псевдосферы, π (3,14…) — математическая константа, выражающая отношение длины окружности к длине ее диаметра, α, β, γ — углы.

Подобных фигур в этих геометриях не существует. Если увеличить стороны в геометрии Лобачевского, углы уменьшатся. Если увеличить стороны фигуры в геометрии Римана, углы увеличатся.

При неизменном радиусе, сумма углов треугольника геометрии Римана при увеличении сторон будет стремиться к 360, то есть к форме полусферы. Сумма углов треугольника геометрии Лобачевского при увеличении сторон будет стремиться к 0.

Отсутствие подобных фигур — одно из самых важных свойств неевклидовых геометрий.

Теорема Пифагора

Без пятого постулата рушится как теорема Пифагора, так и вся классическая тригонометрия.

Без пятого постулата теорема Пифагора, как и тригонометрия, не может существовать, ведь прямоугольный треугольник не будет таким, каким мы его представляем. Вся теорема Пифагора в неевклидовых геометриях, как и формулы площади, будет зависеть от углов. В этих геометриях может быть любой дефект плоскости, поэтому одна сторона треугольника может оказаться больше двух других, значит и теоремы, связанные со сторонами фигур, работать не будут.

Это наиболее известные теоремы, которые существуют в геометрии Евклида, но не могут существовать в геометриях Лобачевского и Римана из-за отрицания пятого постулата.

2.2. Теоремы и аксиомы стереометрии

Для того, чтобы построить объемные фигуры, для начала нужно разобраться, могут ли они вообще существовать. Для этого я предлагаю перечислить некоторые теоремы и аксиомы стереометрии и проверить, нет ли в них свойств, противоречащих свойствам неевклидовых геометрий.

Аксиома 1

Через три точки, не лежащие на одной прямой, проходит плоскость и притом только одна.

Данная аксиома не противоречит постулатам гиперболической и сферической геометрий, соответственно, по первой аксиоме мы можем сказать, что объемные фигуры в неевклидовых геометриях могут существовать.

Аксиома 2

Если две точки прямой лежат в плоскости, то и все точки прямой лежат в этой плоскости.

Эта аксиома не противоречит постулату о параллельных прямых, соответственно, то же верно для рассматриваемых геометрий.

Аксиома 3

Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

Эта теорема является наиболее важной, потому что в ней рассматривается пересечение плоскостей. Она тоже не противоречит теории о параллельности. Только прямая, по которой пересекаются плоскости, будет изогнутой с точки зрения Евклидовой геометрии.

2.3. Свойства объемных фигур неевклидовых геометрий

В предыдущей главе мы доказали, что в гиперболической и сферической геометриях могут существовать трехмерные фигуры.

Сейчас попробуем разобраться в их свойствах.

1) Для начала следует выделить, что стороны объемных фигур будут строиться на различных плоскостях. Трехмерные фигуры будут состоять из двухмерных.

2) Как было упомянуто ранее, площади двухмерных фигур вычисляются при помощи углов и радиуса плоскости.

Объем и площадь трехмерной фигуры, так же, будут вычисляться с использованием углов и радиуса.

3) Объем фигуры будет зависеть от радиуса плоскости, следовательно, подобных фигур, построенных на плоскостях одинакового радиуса, как и в двухмерном пространстве, существовать не может.

3. Построение.

3.1. Пересечение плоскостей.

В сферической и гиперболической геометриях объемные фигуры будут строиться так же, как и в Евклидовой геометрии, то есть каждая сторона фигуры будет задавать плоскость.

Одна фигура может располагаться на плоскостях разного радиуса, в таком случае ее стороны будут иметь различную кривизну, в зависимости от кривизны плоскости.

Для построения трехмерной фигуры требуется как минимум три плоскости. Количество плоскостей зависит от количества сторон фигуры.

3.2. Фигуры в геометрии Римана

Предлагаю посмотреть, как будут выглядеть объемные фигуры в геометрии Римана.

Построим тетраэдр.

Стороны тетраэдра находятся на четырех различных плоскостях, то есть на четырех сферах (рис. 3).

Стороны данного тетраэдра — сферические треугольники, построенные на плоскости геометрии Римана.

Рис. 3

Все эти сферы в данном примере имеют одинаковый радиус, соответственно стороны треугольника равны: они имеют одинаковую площадь, сумму углов, длины сторон и кривизну.

Полученный тетраэдр можно назвать правильным.

4. Формулы для неевклидовых геометрий

Попробуем вывести формулы для площади поверхности и объема гиперболического и сферического тетраэдров, а также для периметра двухмерного треугольника. Для этого воспользуемся формулами площади фигур в геометриях Лобачевского и Римана и некоторыми формулами из элементарной геометрии.

Сферический и гиперболический тетраэдры, как и в евклидовой геометрии, состоят из четырех треугольников. Площадь поверхности правильного тетраэдра можно найти, если умножить площадь треугольника (одной стороны тетраэдра) на 4 (на количество сторон).

Таким образом, получаем формулы для геометрии Римана (3) и для геометрии Лобачевского (4).

S=4R ² (π-α-β-γ) (3)

3.1 Площадь поверхности

S=4R ² (α+β+γ-π),(4)

где S — площадь поверхности тетраэдра, R — радиус сферы и псевдосферы, π (3,14…) — математическая константа, выражающая отношение длины окружности к длине ее диаметра, α, β, γ — углы. В π радианах содержится 180°. Углы следует также перевести в радианы, чтобы можно было умножать их на сантиметры.

Данные формулы подходят для правильных фигур, для всех остальных следует складывать площади двухмерных фигур, а не умножать их на 4.

3.2 Периметр треугольника.

Для начала выведем формулу для периметра сферического треугольника.

Представим плоскость геометрии Римана — сферу. Правильный треугольник с суммой углов 360° занимает половину плоскости, то есть является полусферой. Периметр такого треугольника будет равен длине окружности (5).

P ₁ =2πR

Правильный треугольник с суммой углов 180° занимает четверть плоскости. Его периметр в два раза меньше, чем периметр предыдущего треугольника.

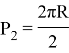
Периметр треугольника и сумма углов находятся в прямой зависимости.

Из вышесказанного делаем вывод, что

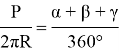
где P — периметр треугольника, π — число пи (3,14…), R — радиус плоскости, α+β+γ — сумма углов треугольника.

Из полученной формулы выразим периметр и переведем градусы в радианы:

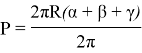
Сократим и получим конечную формулу:

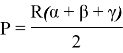
Выведем формулу для гиперболического треугольника.

Плоскость — псевдосфера. Правильный треугольник с суммой углов, близкой к 0°, занимает половину псевдосферы, то есть его периметр равен длине окружности.

Правильный треугольник с суммой углов 180° занимает четверть псевдосферы, то есть его периметр в два раза меньше длины окружности.

Делаем вывод, что сумма углов и периметр находятся в обратной зависимости.

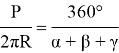
Выразим периметр и преобразуем 360°:

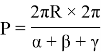
Получим конечную формулу:

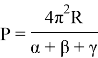
Таким образом, мы вывели формулы периметра для треугольников Лобачевского и Римана.

4.3. Объем

Для вывода формулы объема следует представить рассматриваемые тетраэдры в геометрии Евклида. Сферический тетраэдр — это сумма евклидового тетраэдра и шарового сегмента. Гиперболический — разность.

Шаровой сегмент — часть шара, отсекаемая от него какой-нибудь плоскостью. Объем шарового сегмента вычисляется по формуле

,

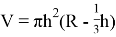
где V — объем шарового сегмента, h — высота сегмента, R — радиус шара.

Объема евклидового тетраэдра вычисляется по формуле:

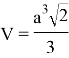
где a — ребро тетраэдра.

Выведем формулу объема сферического тетраэдра:

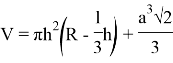
Формула объема гиперболического тетраэдра:

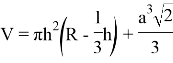
Основанием шарового сегмента является круг, а мы рассматриваем треугольники, поэтому данные формулы дадут примерные значения. Для более точных вычислений стоит использовать интеграл.

5. Заключение

В этом проекте при помощи знаний из евклидовой геометрии было доказано, что в геометриях Лобачевского и Римана могут существовать трехмерные фигуры.

Были выведены свойства для этих фигур, рассмотрен сферический тетраэдр.

При помощи формул площади для сферического и гиперболического треугольников были выведены формулы площади поверхности, объема и периметра треугольника.

Литература:

1. Википедия.
2. Видео на портале Youtube по ссылке: https://www.youtube.com/watch?v=ZlhdzGU9ySE
3. Учебник геометрии 7–9 класс, Атанасян Л. С.
4. Учебник геометрии 10–11 класс, Атанасян Л. С.