Уравнение Ван-дер-Ваальса является простейшей формой уравнения состояния реальных газов, которое качественно правильно описывает поведение реального газа, включая фазовые переходы.
Рассмотрим простой метод получения уравнения Ван-дер-Ваальса [1].
Известно, что по мере увеличения плотности газа, его свойства все более отклоняются от свойств идеального газа и, в конце концов, наступает его конденсация в жидкость. Эти явления связаны со сложными молекулярными взаимодействиями и нет способа, которым можно было бы учесть эти взаимодействия количественным образом с тем, чтобы теоретически построить уточное уравнение состояния вещества. Тогда можно построить уравнение состояния, учитывающее основные качественные особенности молекулярного взаимодействия. Рассмотрим кратко эти особенности.
- Особенности молекулярного взаимодействия
Силы взаимодействия между атомами, приводящие к образованию молекул, имеют в основном электрическое происхождение. Но образование молекул, как и структура атомов, относится к категории квантовых явлений, которые не могут быть объяснены в рамках классической механики.
Простейшей молекулой является двухатомная молекула, состоящая из двух атомов — одинаковых или различных. Взаимодействие атомов, приводящее к образованию такой молекулы, описывается потенциальной энергией, график которой изображен на рис. 1. На этом графике отложена потенциальная энергия ![]() взаимодействия двух атомов как функция расстояния
взаимодействия двух атомов как функция расстояния ![]() между ними (точнее, расстояния между ядрами атомов). Эта функция имеет довольно глубокий и резкий минимум при некотором значении
между ними (точнее, расстояния между ядрами атомов). Эта функция имеет довольно глубокий и резкий минимум при некотором значении ![]() . На меньших расстояниях кривая очень круто поднимается вверх. Эта область соответствует сильному отталкиванию атомов, обусловленному в основном кулоновским отталкиванием сближающихся ядер. Более строгое объяснение природы отталкивания учитывает перекрытие электронных облаков атомов при их сближении и возникновение отталкивания за счет повышения энергии системы, вызванного переходом электронов на более высокие энергетические уровни за счет действия принципа Паули.
. На меньших расстояниях кривая очень круто поднимается вверх. Эта область соответствует сильному отталкиванию атомов, обусловленному в основном кулоновским отталкиванием сближающихся ядер. Более строгое объяснение природы отталкивания учитывает перекрытие электронных облаков атомов при их сближении и возникновение отталкивания за счет повышения энергии системы, вызванного переходом электронов на более высокие энергетические уровни за счет действия принципа Паули.
На больших расстояниях атомы притягиваются. Природа сил притяжения связана с взаимодействием электрических моментов, которые атомы наводят друг на друге.
Расстояние ![]() отвечает устойчивому равновесному взаимному положению ядер в молекуле. В действительности ядра не занимают строго эти положения, а совершают около них колебания. Амплитуда этих колебаний обычно мала. Глубина
отвечает устойчивому равновесному взаимному положению ядер в молекуле. В действительности ядра не занимают строго эти положения, а совершают около них колебания. Амплитуда этих колебаний обычно мала. Глубина ![]() потенциальной ямы характеризует прочность связи атомов в молекуле. Различные молекулы тоже взаимодействуют друг с другом. Это взаимодействие называют ван-дер-ваальсовым, в отличие от химического взаимодействия атомов, приводящего к образованию молекул.
потенциальной ямы характеризует прочность связи атомов в молекуле. Различные молекулы тоже взаимодействуют друг с другом. Это взаимодействие называют ван-дер-ваальсовым, в отличие от химического взаимодействия атомов, приводящего к образованию молекул.
Взаимодействие молекул нельзя, вообще говоря, изобразить просто в виде кривой ![]() , как в случае атомов. Это связано с тем, что взаимное расположение молекул характеризуется большим числом параметров. Так, наряду с расстоянием
, как в случае атомов. Это связано с тем, что взаимное расположение молекул характеризуется большим числом параметров. Так, наряду с расстоянием ![]() между молекулами существенна также и их взаимная ориентация. Но если представить себе взаимодействие молекул как бы усредненным по всем возможным их ориентациям, то оно тоже может быть изображено в виде такой кривой.
между молекулами существенна также и их взаимная ориентация. Но если представить себе взаимодействие молекул как бы усредненным по всем возможным их ориентациям, то оно тоже может быть изображено в виде такой кривой.
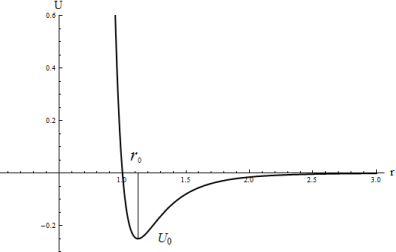
Рис. 1 Потенциальная энергия![]() взаимодействия двух атомов как функция расстояния
взаимодействия двух атомов как функция расстояния ![]() между ними
между ними
Эта кривая похожа на кривую взаимодействия атомов в молекуле в том отношении, что на больших расстояниях все молекулы притягиваются друг к другу, а на малых расстояниях — отталкиваются. Силы притяжения между молекулами быстро убывают с увеличением расстояния между ними. Еще быстрее происходит увеличение сил отталкивания при сближении молекул. Можно себе представить, что при сближении молекулы ведут себя как твердые, взаимно не проникающие тела. Глубина же минимума на кривой ван-дер-ваальсовского взаимодействия очень мала. Она измеряется несколькими десятыми или даже сотыми долями электрон-вольта, в то время как глубина потенциальной ямы на кривой химического взаимодействия между атомами составляет несколько электрон-вольт.
Другое существенное отличие между обоими видами взаимодействия состоит в том, что ван-дер-ваальсовы силы, в отличие от химических, не обладают свойством насыщаемости. Ван-дер-ваальсово взаимодействие существует между всеми молекулами, так что если две молекулы сближаются друг с другом благодаря этому взаимодействию, то они продолжают притягивать и другие молекулы. Поэтому силы молекулярного взаимодействия не приводят к образованию «сверхмолекул», а только содействуют общему стремлению молекул сблизиться друг с другом. Это стремление осуществляется при переходе вещества в конденсированное состояние — жидкое или твердое.
- Получение уравнения Ван-дер-Ваальса
Быстро возрастающие на малых расстояниях силы отталкивания означают, грубо говоря, что молекулы как бы занимают некоторый определенный объем, дальше которого газ не может быть сжат. Другое основное свойство взаимодействия молекул заключается в притяжении на больших расстояниях. Это притяжение очень существенно, поскольку именно оно приводит к конденсации газа в жидкость.
Начнем с того, что учтем в уравнении состояния (для одного моля вещества) ограниченную сжимаемость газа. Для этого надо в уравнении идеального газа
![]() (1)
(1)
заменить объем ![]() разностью
разностью ![]() , где –характерная для данного газа положительная постоянная, учитывающая размеры молекул и занимаемый молекулами объем. Конечность размеров молекул приводит к уменьшению объема, доступного для их движения. Эти соображения приводят к уравнению
, где –характерная для данного газа положительная постоянная, учитывающая размеры молекул и занимаемый молекулами объем. Конечность размеров молекул приводит к уменьшению объема, доступного для их движения. Эти соображения приводят к уравнению
![]() . (2)
. (2)
Из него следует, что объем не может быть сделан меньшим, чем ![]() , поскольку при
, поскольку при ![]() давление обращается в бесконечность. Учтем теперь притяжение молекул. Это притяжение должно приводить к уменьшению давления газа, поскольку на каждую молекулу, находящуюся вблизи стенки сосуда, будет действовать со стороны остальных молекул сила, направленная внутрь сосуда. В грубом приближении эта сила будет пропорциональна числу молекул в единице объема, т. е. плотности газа. С другой стороны, давление само пропорционально этому же числу. Поэтому общее уменьшение давления, связанное с взаимным притяжением молекул, будет пропорционально квадрату плотности газа, т. е. обратно пропорционально квадрату его объема.
давление обращается в бесконечность. Учтем теперь притяжение молекул. Это притяжение должно приводить к уменьшению давления газа, поскольку на каждую молекулу, находящуюся вблизи стенки сосуда, будет действовать со стороны остальных молекул сила, направленная внутрь сосуда. В грубом приближении эта сила будет пропорциональна числу молекул в единице объема, т. е. плотности газа. С другой стороны, давление само пропорционально этому же числу. Поэтому общее уменьшение давления, связанное с взаимным притяжением молекул, будет пропорционально квадрату плотности газа, т. е. обратно пропорционально квадрату его объема.
В соответствии с этими соображениями, вычтем из предыдущего выражения для давления член вида ![]() , где
, где ![]() – некоторая новая постоянная, характеризующая силы молекулярного притяжения. Таким образом, получим уравнение Ван-дер-Ваальса:
– некоторая новая постоянная, характеризующая силы молекулярного притяжения. Таким образом, получим уравнение Ван-дер-Ваальса:
![]() , (3)
, (3)
или, в несколько другом виде
![]() . (3*)
. (3*)
При большом разрежении газа (большие объемы ![]() ) величинами
) величинами![]() и
и ![]() можно пренебречь, и уравнение Ван-дер-Ваальса возвращаемся к уравнению состояния идеального газа.
можно пренебречь, и уравнение Ван-дер-Ваальса возвращаемся к уравнению состояния идеального газа.
Для проведения количественных расчетов на основе уравнения Ван-дер-Ваальса необходимо определить величины постоянных ![]() и
и ![]() . Простейшим вариантом является определение этих постоянных из соотношений, связывающих их с критическими параметрами вещества — температурой, давлением и объемом в критической точке. Величины постоянных являются функциями температуры и подобрать их таким образом, чтобы получить согласие с экспериментальными данными во всем диапазоне параметров невозможно [2, 3]. Поэтому уравнение Ван-дер-Ваальса используется в основном для качественного анализа поведения вещества.
. Простейшим вариантом является определение этих постоянных из соотношений, связывающих их с критическими параметрами вещества — температурой, давлением и объемом в критической точке. Величины постоянных являются функциями температуры и подобрать их таким образом, чтобы получить согласие с экспериментальными данными во всем диапазоне параметров невозможно [2, 3]. Поэтому уравнение Ван-дер-Ваальса используется в основном для качественного анализа поведения вещества.
Принципиальное значение уравнения Ван-дер-Ваальса определяется следующими обстоятельствами:
1) Уравнение было получено из модельных представлений о свойствах реальных газов и жидкостей, а не явилось результатом эмпирического подбора функции ![]() , описывающей свойства реальных газов.
, описывающей свойства реальных газов.
2) Уравнение долго рассматривалось как некоторое исходное уравнение состояния реальных газов, на основе которого было построено много других уравнений состояния.
3) С помощью уравнения Ван-дер-Ваальса впервые удалось описать явление перехода газа в жидкость и проанализировать критические явления. В этом отношении уравнение Ван-дер-Ваальса имеет преимущество даже перед более точными уравнениями в вириальной форме.
- Аналитическое исследование свойств газа Ван-дер-Ваальса
Для исследования поведения газа, описываемого уравнением Ван-дер-Ваальса, рассмотрим определяемые этим уравнением изотермы, т. е. кривые зависимости давления от объема при постоянных значениях температуры. С этой целью перепишем уравнение Ван-дер-Ваальса в виде
![]() . (1.4)
. (1.4)
При фиксированных значениях ![]() и
и ![]() это — уравнение третьей степени относительно переменной
это — уравнение третьей степени относительно переменной ![]() . Как известно, уравнение третьей степени имеет три корня, из них вещественными могут быть либо все три, либо только один. Физический смысл имеют только вещественные и положительные корни (объем
. Как известно, уравнение третьей степени имеет три корня, из них вещественными могут быть либо все три, либо только один. Физический смысл имеют только вещественные и положительные корни (объем ![]() ). Отметим, что уравнение не может иметь отрицательных вещественных корней, т. к. в этом случае все слагаемые имели бы отрицательный знак и не могли бы в сумме дать ноль. Отметим, что заданным значениям давления и температуры по уравнению Ван-дер-Ваальса соответствуют либо три различных значения объема, либо только одно.
). Отметим, что уравнение не может иметь отрицательных вещественных корней, т. к. в этом случае все слагаемые имели бы отрицательный знак и не могли бы в сумме дать ноль. Отметим, что заданным значениям давления и температуры по уравнению Ван-дер-Ваальса соответствуют либо три различных значения объема, либо только одно.
Второй случай имеет место при достаточно высоких температурах. Соответствующие изотермы отличаются от изотерм идеального газа лишь некоторым изменением их формы, но остаются монотонно спадающими кривыми. При более низких температурах изотермы имеют максимум и минимум, так что для каждой из них существуют такие интервалы давлений, в которых кривая определяет три различных значения ![]() . На рис. 2 изображена одна из таких изотерм. Разберем физический смысл различных ее участков.
. На рис. 2 изображена одна из таких изотерм. Разберем физический смысл различных ее участков.
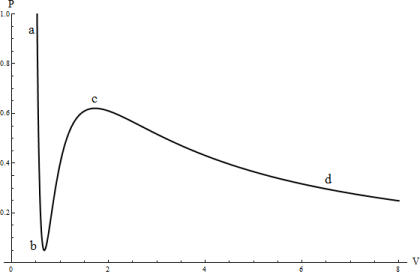
Рис. 2 Изотерма уравнения Ван-дер-Ваальса
На участках ![]() и
и ![]() зависимость давления от объема имеет нормальный характер, т. е. давление возрастает при уменьшении объема. Участок же
зависимость давления от объема имеет нормальный характер, т. е. давление возрастает при уменьшении объема. Участок же ![]() соответствовал бы неестественному положению, когда сжатие вещества приводило бы к уменьшению давления. Такие состояния не могут осуществляться в природе.
соответствовал бы неестественному положению, когда сжатие вещества приводило бы к уменьшению давления. Такие состояния не могут осуществляться в природе.
Наличие заведомо неосуществимого участка ![]() изотермы означает, что при постепенном изменении объема вещество не может оставаться все время в виде однородной среды. В некоторый момент времени должно наступать скачкообразное изменение состояния и распад вещества на две фазы. Другими словами, истинная изотерма будет иметь вид ломаной линии
изотермы означает, что при постепенном изменении объема вещество не может оставаться все время в виде однородной среды. В некоторый момент времени должно наступать скачкообразное изменение состояния и распад вещества на две фазы. Другими словами, истинная изотерма будет иметь вид ломаной линии ![]() , как показано на рис. 3. Часть ее отвечает газообразному состоянию вещества, а часть — жидкому состоянию. Горизонтальный же прямолинейный отрезок соответствует двухфазным состояниям — переходу газа в жидкость, происходящему (при заданной температуре) при определенном постоянном давлении.
, как показано на рис. 3. Часть ее отвечает газообразному состоянию вещества, а часть — жидкому состоянию. Горизонтальный же прямолинейный отрезок соответствует двухфазным состояниям — переходу газа в жидкость, происходящему (при заданной температуре) при определенном постоянном давлении.
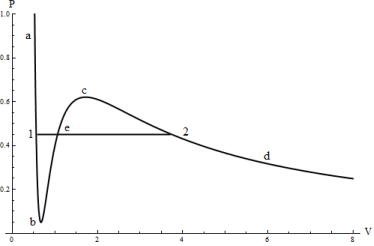
Рис. 3 Изотерма уравнения Ван-дер-Ваальса и изотерма реального газа
Что касается участков изотермы ![]() и
и ![]() , то они отвечают метастабильным состояниям — переохлажденному пару и перегретой жидкости. Видно, что существуют определенные границы (изображаемые точками
, то они отвечают метастабильным состояниям — переохлажденному пару и перегретой жидкости. Видно, что существуют определенные границы (изображаемые точками ![]() и
и ![]() ), дальше которых переохлаждение пара или перегрев жидкости вообще невозможны.
), дальше которых переохлаждение пара или перегрев жидкости вообще невозможны.
При повышении температуры прямолинейный участок изотермы уменьшается и при критической температуре стягивается в одну точку. Проходящая через эту точку изотерма разделяет изотермы обоих типов: монотонные изотермы и изотермы с максимумами и минимумами, на которых неизбежно распадение вещества на две фазы.
Если соединить между собой точки начала и конца прямолинейных отрезков изотерм, то получающаяся кривая представит собой кривую фазового равновесия жидкости и пара на диаграмме ![]() ,
, ![]() . Максимум этой кривой есть критическая точка. В этом состоянии система с макроскопической точки зрения представляет собой одну фазу.
. Максимум этой кривой есть критическая точка. В этом состоянии система с макроскопической точки зрения представляет собой одну фазу.
В критической точке сливаются в одну три точки, в которых прямолинейный участок пересекает изотеру Ван-дер-Ваальса. Отсюда следует, что касательная к изотерме в критической точке имеет горизонтальное направление, т. е. обращается в ноль производная от давления по объему (при постоянной температуре):
![]() . (5)
. (5)
Величина, обратная этой производной, есть сжимаемость вещества. Таким образом, в критической точке сжимаемость вещества обращается в бесконечность. Отметим, что параметры уравнения Ван-дер-Ваальса ![]() и
и ![]() можно найти, зная давление, объем и температуру в критической точке. Для нахождения критических параметров
можно найти, зная давление, объем и температуру в критической точке. Для нахождения критических параметров ![]() ,
, ![]() ,
, ![]() заметим, что уравнение Ван-дер-Ваальса в критической точке можно записать в виде
заметим, что уравнение Ван-дер-Ваальса в критической точке можно записать в виде
![]() . (6)
. (6)
Поскольку в этом случае все три корня совпадают и равны ![]() , уравнение должно приводиться к виду:
, уравнение должно приводиться к виду:
![]() . (7)
. (7)
Возводя в куб и сравнивая коэффициенты двух последних уравнений, получим три уравнения: ![]() ,
, ![]() ,
, ![]() .
.
Решая их, найдем
![]() ,
, ![]() ,
, ![]() . (8)
. (8)
К тем же результатам можно прийти, заметив, что критическая точка является точкой перегиба изотермы, поэтому, кроме первой производной в ней должна обращаться в ноль и вторая производная давления по объему:
![]() ,
, 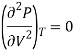 . (9)
. (9)
Вычисляя эти производные из уравнения Ван-дер-Ваальса и, решая полученную систему уравнений, придем к тем же результатам. И наоборот, зная из эксперимента критические параметры вещества, можно определить постоянные Ван-дер-Ваальса:
![]() ,
, 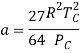 . (10)
. (10)
Одним из параметров, характеризующих качество уравнения состояния реального газа, является вычисленный на его основе критический коэффициент ![]() :
:
![]() . (11)
. (11)
Подставляя сюда полученные выше выражения критических параметров через постоянные Ван-дер-Ваальса, получим ![]() . Таким образом, критический коэффициент получается одинаковым для всех веществ. В действительности для разных веществ
. Таким образом, критический коэффициент получается одинаковым для всех веществ. В действительности для разных веществ ![]() имеет различные значения, причем они всегда больше 2,67 и имеют в среднем значение 3,7.
имеет различные значения, причем они всегда больше 2,67 и имеют в среднем значение 3,7.
Литература:
- Ландау Л. Д., Лифшиц Е. М. Курс общей физики. Механика и молекулярная физика. — М.: Наука, 1965. — 384 с.
- Таблицы физических величин. Справочник. Под ред. акад. И. К. Кикоина. –М.: Атомиздат, 1976. — 1008 с.
- Каханер Д., Моулер К., Нэш С. Численные методы и математическое обеспечение: Пер. с англ. — М.: Мир, 1998. — 575 с.

