Исследованию существенного спектра модельных непрерывных и дискретных операторов Шредингера посвящены многие работы (см. например, [1] и [2], соответственно). Обычно в физической литературе используется “локальные” потенциалы, т. е. операторы умножения на функцию. Однако потенциалы, которые строятся, например, в теории псевдопотенциала оказываются нелокальными и представляют собой, в том числе для периодического оператора, сумму локального потенциала и некоторого конечномерного. В настоящей работе рассматривается модельный оператор Н, как сумма оператор умножения и частично интегрального оператора. Рассмотрим модельный оператор Н, действующий в гильбертовом пространстве 
по формуле 
где 
— есть оператор умножения, а V — частично-интегральный оператор:
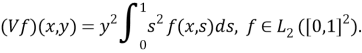
Можно проверить, что в этом случае оператор Н, является ограниченным и самосопряженным оператором в гильбертовом пространстве 
. Для формулировки основного результата настоящей работы наряду с оператором Н рассмотрим также ограниченную и самосопряженную модель Фридрихса 
, действующую в 
как
, где операторы 
и v определяются по правилам
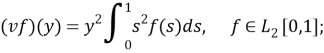
Видно, что оператор v является одномерным. Поэтому
Теперь перейдем к изучению дискретного спектра оператора 
. Пусть С- комплексная плоскость. При каждом фиксированном 
определим регулярную в 
функцию
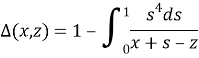
Тогда легко проверяется, что
Основным результатом настоящей работы является следующая теорема.
Теорема 1. Оператор Н имеет чисто существенный спектр и для него имеет место равенство
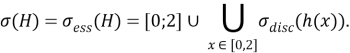Доказательство. Сперва докажем, что 
Пусть 
— произвольная точка. Покажем, что 
Для этого удобно воспользоваться критерием Вейля [1], т. е. достаточно построить последовательность ортонормированных векторов 
, для которых 
Так как 
– непрерывная функция в компактном множестве т. е. в квадрате 
, существует точка 
такая, что 
. Рассмотрим следующую окрестность точки :
,
где
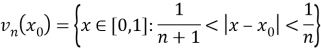— выколотая окрестность точки 
.Пусть µ(
) — мера Лебега множества .
Последовательность 
выбираем следующим образом:
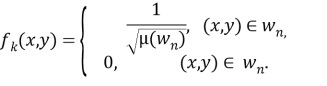
Очевидно, что –ортонормированная последовательность.
Рассмотрим (H-
)
и оценим его норму:
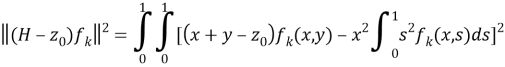
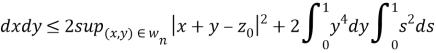
Из построения множества 
следует 
, 
. В силу непрерывности функции 
имеем, что
.
Тем самым доказано, что 
, т. е. 
.
Из произвольности точки следует, что 
.
Включение.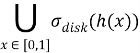 
доказывается аналогично. А обратное утверждение, т. е. факт
доказывается с помощью уравнения Фаддеева для собственных вектор функций оператора H.
Литература:
1. Г. М. Жислин. Труды ММО, 9, 1960, 81–120.
2. S. Albeverio, S. N. Lakaev, Z. J. Muminov, Russ. J. Math.Phys., 14:4 (2007), 377–387.
