Политропным процесс называют процесс, протекающий при постоянной теплоемкости . Политропические процессы часто встречаются на практике, почему они и представляют интерес, в частности, политропическим процессом является адиабатный процесс, т. е. когда тепло не подводится к системе () и она предоставлена сама себе. Конечно, политропический процесс достаточно лаконично записан для модели идеального газа, но в случае практики модель идеального газа хорошо себя показывает лишь в случае с небольшими давлениями и большими температурами, в дальнейшем газ намного лучше описывается множеством уравнений для реального газа. Наиболее компактную форму имеет уравнение Ван-дер-Ваальса, также оно одно из самых широко известных, поэтому попробуем описать уравнение политропы для реального газа как раз с помощью него.

Ключевые слова: идеальный газ, реальный газ, политропический процесс, адиабатный процесс, RTV, уравнение политропы.

Вывод уравнения политропического процесса модели Ван-дер-Ваальса

1) Запишем уравнение Ван-дер-Ваальса для молей газа: [2]

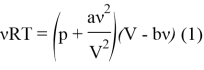
Заметим, что в случае (заметим, что запись — некорректно, из-за размерности коэффициентов), уравнение Ван-дер-Ваальса приобретает вид уравнения идеального газа.

2) В случае реального газа внутренняя энергия складывается из потенциальной энергии взаимодействия молекул, а также ее кинетической составляющей:

Выражение для не меняется при переходе от идеального к реальному газу:

За наличие сил притяжения отвечает поправка , а потенциальная составляющая есть работа, растрачиваемая при «разбросе» молекул газа на бесконечность, т. е.:

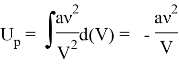
Окончательное выражение для внутренней энергии реального газа:

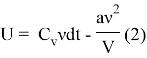
3) Запишем первый закон термодинамики:

Рассмотрим небольшое изменение объема, так что давление газа практически не изменится и будет верна формула:

Подставляя все полученное нами выше в первый закон термодинамики, мы получим:

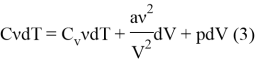
4) Выразим давление из (1):

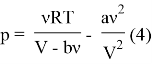
5) Учитывая (3) и (4) получим, что:

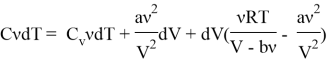
Упрощая данное выражение имеем:

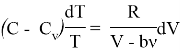
Проинтегрируем полученное нами выражение:

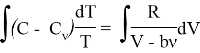
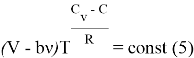
Выражение (5) является уравнением политропы для газа модели Ван-дер-Ваальса в зависимости . Уточним, что в правой части зависит от начальных параметров нашей системы.

Учитывая (1) и (5) выведем уравнение политропы

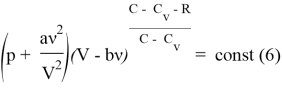
Заметим, что мы не можем «схлопнуть» , так как для реального газа: [1]

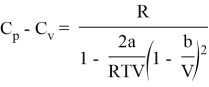
Обобщение на идеальный газ

В случае идеального газа мы получим уравнение политропного процесса для него, так что формула (6) есть обобщение политропического процесса как для идеального, так и для реального газов.

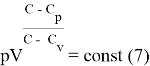
Оценка расхождения уравнения политропы для реального иидеального газов

Для идеального газа

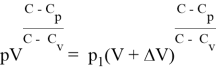
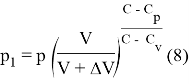
Для реального газа

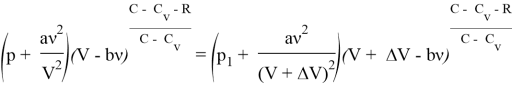
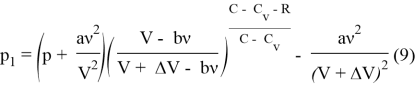
Рассмотрим адиабатный процесс, протекающий над одним молем азота , начальным давлением в 50 бар и начальным объемом в 1л. Будем откладывать на оси давление и объем и построим три графика: зависимость (8), зависимость (9), а так же разницу давлений при одинаковых объемах, т. е. проведём численное моделирование.

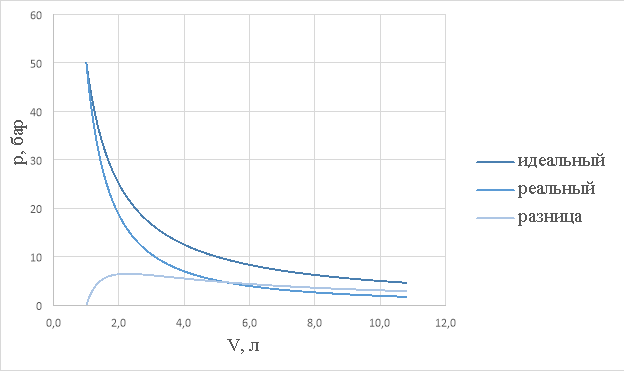
Рис.1.

Заметим из рис.1, что отличия есть и по началу они существенны, но при уменьшении давления графики «сближаются» друг к другу, что так же подтверждается экспериментальными данными. (в действительности, благодаря экспериментам мы знаем, что модель идеального газа хорошо описывает реальный газ при малых давлениях и больших температурах)

Литература:

1. О разности 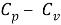газа Ван-дер-Ваальса. Булыгин В. С., 26 июня 2011 г.
2. Сивухин Д. В. Общий курс физики.