Фракталы в электротехнике
Автор: Кондрашов Илья Александрович
Рубрика: Электротехника
Опубликовано в Техника. Технологии. Инженерия №1 (1) июнь 2016 г.
Дата публикации: 23.05.2016
Статья просмотрена: 2070 раз
Библиографическое описание:
Кондрашов, И. А. Фракталы в электротехнике / И. А. Кондрашов. — Текст : непосредственный // Техника. Технологии. Инженерия. — 2016. — № 1 (1). — С. 30-34. — URL: https://moluch.ru/th/8/archive/36/933/ (дата обращения: 27.10.2024).
Фрактал (лат. fractus — дроблёный, сломанный, разбитый) — геометрическая фигура, обладающая свойством самоподобия, то есть составленная из нескольких частей, каждая из которых подобна всей фигуре целиком. Фрактазм — самостоятельная точная наука изучения и составления фракталов.Фракталы известны уже почти век, хорошо изучены и имеют многочисленные приложения в жизни. В основе этого явления лежит очень простая идея: бесконечное по красоте и разнообразию множество фигур можно получить из относительно простых конструкций при помощи всего двух операций — копирования и масштабирования. Различают динамические и геометрические фракталы. Причём теория фракталов благодаря учёным и энтузиастам вышла за пределы математики и теперь используется как применительно к техническим наукам, так и в искусстве.
Довольно интересным проявлением фракталов в искусстве является переложение графиков финансового кризиса на музыку немецким музыкантом-экспериментатором Йоханнесом Крайдлером. Музыкант присвоил определенные ноты колеблющимся индексам. Так что благодаря его творческой обработке теперь можно услышать, с каким звуком «падали» Lehman Brothers, Genereral Motors и Bank of America.
Фракталы также используются в теории информации при разработке методов сжатия данных (например, при сжатии графических данных в основном применяется свойство самоподобия фракталов — для запоминания небольшого фрагмента рисунка и преобразования, с помощью которых можно получить остальные части, требуется гораздо меньше памяти, чем для хранения всего файла). В условиях современной тенденции к росту объёма различного рода данных применение фрактального сжатия представляет интерес. Тем не менее, теория фракталов может иметь и другие научно-технические приложения. Уже сейчас фрактальные структуры можно наблюдать в различных областях электротехники и радиотехники.
Фрактальные антенны — относительно новый класс электрически малых антенн (ЭМА), принципиально отличающийся своей геометрией от известных решений. По сути, традиционная эволюция антенн базировалась на евклидовой геометрии, оперирующей объектами целочисленной размерности (линия, круг, эллипс, параболоид и т. п.) [1]. Моделирование и эксперименты показывают, что фрактальные антенны позволяют получить практически такой же, как и у обыкновенных антенн, коэффициент усиления. Однако габариты фрактальных антенн гораздо меньше, соответственно и размер радиоэлектронного изделия может быть уменьшен, а это важно для мобильных устройств. Считается, что изучение возможности применения фракталов в приёмо-передающих устройствах началось в 80-х годах 20-го века.
Наиболее интересным для дальнейшего рассмотрения имеет фрактал, называемый кривой Коха (рисунок 1), которая относится к виду геометрических фракталов.
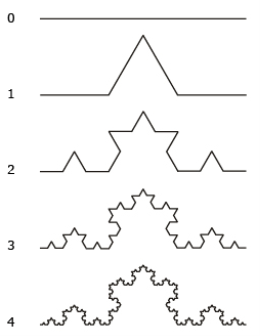
Рис. 1. Построение кривой Коха
Математически длина полученной в результате некоторого числа итераций кривой может быть найдена по формуле:
![]() ,(1)
,(1)
гдеh — длина исходного отрезка;
n — число итераций.
На рисунке 2 представлена фрактальная антенна, выполненная в виде ранее приведённой кривой Коха [2]. Следует заметить, что антенна формы кривой Коха — это не единственное возможное выполнение фрактальной антенны [1]. В качестве отдельных устройств приёмо-передающей аппаратуры могут использоваться элементы имеющие форму кривых Пеано, например оригинальной кривой Пеано (рисунок 3) или рекурсивной кривой Пеано (рисунок 4).

Рис. 2. Фрактальная антенна в форме кривой Коха
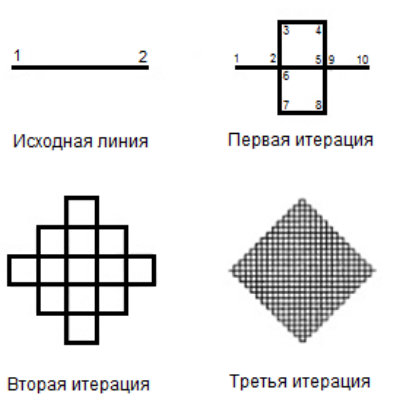
Рис. 3. Построение кривой Пеано

Рис. 4. Построение рекурсивной кривой Пеано
Антенна, форма которой частично построена на основе рекурсивной кривой Пеано, приведена на рисунке 5 [3].

Рис. 5. Экспериментальная фрактальная антенна
В целом следует отметить, что теоретически представить механизм взаимодействия фрактальной приемной антенны и падающих на нее электромагнитных волн сложно из-за отсутствия аналитического описания волновых процессов в проводнике со сложной топологией [1]. В силу вышеупомянутого важными факторами в изучении фрактальных антенн является математическое моделирование и эксперимент.
Также в качестве фрактала можно рассматривать структуру графена. Этот материал, как известно, состоит из шестиугольных ячеек, соединенных между собой, именно это напоминает фрактальную структуру (рисунок 6). Графен обладает выдающимися физическими и электротехническими характеристиками. Помимо усовершенствования известных устройств, использование графена поможет создать принципиально новые изделия.
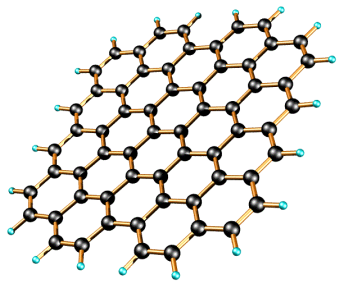
Рис. 6. Структура графена
Литература:
- В.Слюсар. Фрактальные антенны [Текст]/ В.Слюсар // Электроника: Наука, Технология, Бизнес. — 2007, № 7.
- Фрактальные антенны своими руками. Сайт: Ваш техник.ru. Режим доступа: http://vashtehnik.ru/radioapparatura
- MOWWA — Fractal antenna experiment. Режимдоступа: http://www.m0wwa.co.uk/page/M0WWA_fractal_antenna.html







