В средней школе на уроках физики школьникам объясняют закон Гука, который представляют наглядным образом, в виде пружины, к которой прикреплен определенный вес. Так нас знакомят не только с законом Гука, но и со свойством многих предметов — с упругостью.
Роберт Гук открыл этот закон, когда рассматривал, как можно улучшить механизм часов. Открытие закона Гука имеет важное значение для физики, т. к. данное событие помогло определять какие материалы упругие, а какие — нет. Данный закон входит в раздел общей механики — статика.
Суть закона Гука можно представить в виде вертикально расположенной пружины, которая прикреплена к потолку, и имеющая крюк, для цепки разных грузов. Начальная длина пружины — x, при прикреплении к ней груза массой — m груз , длина пружины стала — x’. Можно заключить, что длина пружины стала больше, а именно на Δx = x’ — х. В начале, после того как мы подкрепили к пружине груз, пружина начинает колебаться. Через некоторое время, данная механическая система приходит в равновесие. Из этого события выходят следующие выводы: сила, производимая на массу тяготением F 1 = m груз g и сила, производимая пружиной, которая старается вернуть ее в начальное положение F 2 равны, но при этом противоположно направлены, т. е. когда система достигает установившегося состояния, то можно сказать, что F 1 = F 2 .
Также в законе Гука можно пронаблюдать, что между силой и удлинением пружины существует линейная зависимость, при помощи воспроизведения опыта с разными массами и с разными пружинами. При этом можно отметить, что есть при опыте с одной пружиной и разными массами, определенный коэффициент, на который отличается удлинение и сила. Этот коэффициент получил название постоянной упругости — k, который зависит от материала пружины и ее геометрической формы. Т. к. возвращающая сила (сила упругости) противонаправлена деформирующей силе, то закон Гука имеет вид:
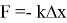
Формулировка закона Гука в общем виде гласит так: сила, стремящаяся вернуть пружину в равновесие, прямо пропорциональна значению ее удлинения по отношению к положению равновесия.
Закон Гука помог понять, что существует такой момент, когда соотношение силы и деформации перестает иметь линейную зависимость — этот момент называется пределом упругости. Наглядно представить можно это явление так, когда к пружине будет прикреплен груз, имеющий настолько большую массу, что пружина не сможет вернуться в исходное положение.
По зависимости силы от деформации можно пронаблюдать, как тот или иной материал будет проявлять свою упругость. Когда материал потерял свою изначальную молекулярную структуру, можно сказать, что это необратимая деформация, а если же, материал разрушается, и его молекулы разделяются, то это уже пластичная деформация.
Сам же закон Гука, был открыт в 17 веке Робертом Гуком, когда он проводил опыты и написал книгу «Кутлеровские лекции», имеющая 6 лекций. В шестой лекции Гук писал об упругости, которая называлась «О восстановительной способности, или Об упругости». Закон Гука оказал значительное влияние на дальнейшие открытия, не только в физике, но и в других сферах. [1, c. 63–93]
Открытие закона Гука имело огромное значение для развития техники и науки. Гук также представил общую картину движения планет, тяготеющих друг к другу. Он смог предвосхитить закон всемирного тяготения Исаака Ньютона, в 1679 году утверждал, что если сила притяжения обратно пропорциональна квадрату расстояния, то планета должна двигаться по эллипсу.
Открытие этого закона, ученные получили хорошую возможность более глубоко и детально изучить процессы деформации и упругости материалов, что привело к созданию новых материалов и технологий, таких как резинообразованные материалы и пружины. Это открытие также оказало влияние на развитие физики, инженерии и многих других областей.
Этот закон помог создать такие устройства, как амортизаторы, которые являются одними из важных элементов системы подвески автомобиля, т. к. оно гасит колебания и поглощает толчки и удары подвижных элементов машины. [5] Также этот закон применяется в механических часах, в котором балансирное колесо оснащено балансирной пружиной, а также спиралью баланса, которая чаще всего состоит из высокоэластичного материала, например, сталь. Согласно закону Гука, пружина растягивается и сжимается, когда баланс колеса колеблется взад-вперед, применяя регулирующее усилие. Это гарантирует, что механизм хронометрирования движется точно и по расписанию. [4]
Закон Гука в области навигации, утверждает, что вероятность корректного интегрирования разнообразных навигационных данных возрастает вместе с увеличением количества источников информации и их независимость друг от друга. Иными словами, чем больше доступных источников и чем больше независимы они друг от друга, тем выше вероятность получения точной информации о местоположении корабля в момент времени.
Этот закон имеет огромное значение для навигации кораблей, поскольку корректное определение местоположения судна на море является критическим для безопасного плавания и предотвращения столкновений. Путем интеграции данных от датчиков GPS, азимутных гироскопов, рулевых компасов, а также других навигационных систем, корабли могут обеспечить себе максимальную точность при определении своего положения на море.
Таким образом, закон Гука является основой для разработки надежных и точных навигационных систем на кораблях, обеспечивая безопасность и эффективность плавания. [2], [3].
Литература:
- Наука. Величайшие теории: выпуск 40: В поисках формы. Гук. Закон Гука. / Пер. с франц. — М.: Де Агостини, 2015. — 168 с.
- Код доступа: https://gufo.me/dict/bse. Дата обращения: 15.06.2024
- Кудрявцев П. С. Курс истории физики. М.: Просвещение, 1982. — 448 с.
- Код доступа: https://www.geeksforgeeks.org/real-life-applications-of-hookes-law/. Дата обращения: 15.06.2024
- Код доступа: https://ru.wikipedia.org/wiki/Амортизатор. Дата обращения 15.06.2024

