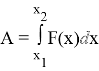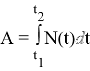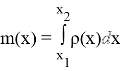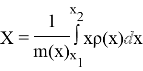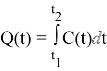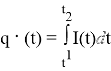Интегральное исчисление как один из аспектов межпредметных связей школьной физики и математики



В современной науке все области тесно взаимосвязаны, что делает невозможным изолированное рассмотрение школьных предметов. Межпредметные связи становятся неотъемлемым дидактическим условием для полного освоения научных дисциплин в школе. Введение таких связей способствует глубокому усвоению знаний, формированию научных понятий и развитию научного мировоззрения. Это подчеркивает единство материального мира, взаимосвязь явлений в природе и обществе, улучшает организацию учебно-воспитательного процесса, делая его более оптимальным и придавая высокое воспитательное значение. Межпредметные связи также важны для развития логического мышления и творческих способностей учащихся, сокращая избыточное изучение материалов и создавая условия для переноса знаний в новые ситуации. Внедрение таких связей между математикой и физикой в основной школе конкретизирует эти выгоды, способствуя повышению качества образования и развитию познавательных интересов учеников.

Отношения между математикой и физикой как научными дисциплинами являются постоянными и многообразными. Чистая математика ориентирована на абстракцию, используя реальный материал, такой как пространственные формы и количественные взаимоотношения материального мира. Однако эти материалы обретают абстрактные формы в процессе математического анализа. Математика, будучи аспектной наукой, охватывает всю действительность, изучая закономерности во всех областях объектов, даже тех, которые могут быть «сконструированы». Физика, в свою очередь, исследует фундаментальные свойства материи в формах вещества и поля. Эти две дисциплины представляют собой сложный комплекс знаний, объединенных общими принципами, фундаментальными теориями и методами исследования. [1].

Исходно физика занималась изучением свойств окружающих объектов, фокусируясь на конкретных телах и явлениях, таких как движение, взаимодействие и структура вещества. Однако в XX веке акцент в физике перешел на изучение фундаментальных явлений природы и разработку соответствующих законов. В этом контексте математика, ставшая неотъемлемой частью физических исследований, приобрела значительное влияние. Взаимосвязь между математикой и физикой обусловлена общей предметной областью, что проявляется в переплетении идей и методов. Математика не только служит инструментом для описания физических явлений, но также является ключевым компонентом в поиске новых путей понимания фундаментальных законов природы.

Эти связи можно условно разделить на три вида, а именно [2]:

1. Физика формулирует задачи и разрабатывает математические концепции и методы, необходимые для их решения, что впоследствии станут основой развитию математической теории.
2. Развитая математическая теория со своими концепциями и инструментарием используется для анализа физических явлений. Этот подход часто выступает катализатором появления новых физических теорий, что, в свою очередь, приводит к качественному расширению представлений о физической природе и возникновению новых физических вопросов.
3. Прогресс в физической теории основывается на существующем математическом инструментарии, который в свою очередь совершенствуется и расширяется с увеличением его применения в области физики.

Курс математики в 10–11 классах обычно включает в себя более глубокое изучение алгебры, начал анализа, геометрии, а также тем, таких как теория вероятностей и математическая статистика. Этот этап образования призван предоставить ученикам более сложные математические инструменты и теории, чтобы подготовить их к получению высшему образованию.

Роль математики как межпредметной связи важна в этом контексте. Математика служит языком, который объединяет различные области знаний. Например, она может быть ключом к пониманию физических законов и явлений:

1. Моделирование физических явлений: Алгебра и анализ предоставляют математические инструменты для моделирования и описания физических процессов. Уравнения и графики, используемые в алгебре, могут отражать законы движения, изменения температуры, электрические цепи и т. д.
2. Решение физических задач: Методы алгебры и анализа могут быть применены для решения конкретных физических задач. Например, использование дифференциальных уравнений для описания изменения физических величин во времени.
3. Понимание фундаментальных концепций: Алгебра и анализ помогают студентам понять основные концепции физики, такие как скорость, ускорение, сила и энергия, переводя их в математический язык.
4. Развитие аналитического мышления: Изучение алгебры и начал анализа развивает аналитическое мышление, что полезно для построения логических цепочек рассуждений в физике.

В этом случае математика приобретает особую ценность как катализатор для создания организованного и точного метода анализа и объяснения физических явлений в рамках программы по физике. Передача знаний между различными научными областями подчеркивает силу научного знания, которая проявляется в логической координации его элементов и универсальности основных принципов.

Овладение основными принципами науки, включая ее философские обобщения и способность выявлять отдельные позиции, применяемые в соответствующих областях знания, является кульминацией структуры знания. В процессе изучения физики большое внимание уделяется изучению различных величин и физических законов, что создает благоприятные условия для обобщения знаний, выявления величин и установления взаимосвязей между ними. Прежде всего, как формирование мировоззрения студента, оно основывается на философском обобщении знаний, полученных в ходе изучения смежных дисциплин. Всестороннее усвоение учебного материала и эффективное формирование соответствующего мышления определяются общими целями, средствами и методами, установленными в системе образовательной деятельности. [3]

Межпредметные связи в практике обучения могут быть внедрены по различным направлениям:

1. Формирование преемственности при изучении понятий: учителям естественно-математического цикла следует внимательно изучать программы и методические пособия сопредельных предметов; определение объема знаний, внесенных каждым предметом, для эффективного формирования у учащихся необходимых понятий и умений.
2. Согласование времени изучения учебных дисциплин: установление рациональной последовательности изучения материала для обеспечения непрерывной понятийной базы и формирования умений для других предметов; реализация на уровне учебного плана общеобразовательной школы для поддержания логики и структуры изучения материала.
3. Обеспечение единства в интерпретации общих понятий: предотвращение «расщепления понятий» через утверждение единого подхода к интерпретации общих понятий, законов и теорий; поддержание единого видения учебных материалов для предотвращения недоразумений в сознании учеников.
4. Раскрытие общих методов научных исследований: введение в учебный процесс методов, таких как наблюдения, умственное моделирование и эксперимент; единый подход к формированию экспериментальных умений и соответствующих требований.
5. Предложение единого подхода к формированию обобщенных способов деятельности: выделение обобщенных познавательных умений, таких как работа с учебной литературой, графические навыки, умение проводить наблюдения и опыты; повышение качества обучения предметам естественно-математического цикла через формирование обобщенных познавательных умений.

Таким образом, суть межпредметных связей заключается в установлении взаимосвязей между учебными дисциплинами, способствующих формированию у учеников общих синтезированных знаний. Систематическая реализация таких связей, например, между математикой и физикой, позволяет повысить качество образования и развития интересов учеников. Так, например, интегральное исчисление является неким мостом между физикой и математикой. В контексте межпредметных связей, интеграл может быть рассмотрен как инструмент, объединяющий абстрактные математические концепции с конкретными приложениями в физике

Интегральное исчисление — это раздел математического анализа, в котором изучаются интегралы, их свойства, способы вычисления и приложение.

Интегральное исчисление возникло из рассмотрения большого числа задач естествознания и математики. Важнейшие из них — физическая задача определения, пройденного за данное время пути по известной, но, быть может, переменной скорости движения и значительно более древняя задача вычисления площадей и объемов геометрических фигур.

Центральным в интегральном исчислении является понятие интеграла, которое, однако, имеет две различные трактовки, приводящие соответственно к понятиям неопределенного и определённого интегралов.

Примеры применения интегралов в курсе школьной физики:

Величины	Физическая зависимость в простейшем случае	Вычисление производной	Вычисление интеграла
A — работа, F — сила, N — мощность, x — пройденный путь, t — время	A=F×x N=A / t	F(x)=A’(x) N(t)=A’(t)
m — масса тонкого стержня, ρ — линейная плотность, x — линейный размер	m=ρ×x	r(x)=m’(x)	координата центра масс стержня
S — перемещение, v — скорость, t — время	v=S / t	v(t)=S’(t)
Q — количество теплоты; с — теплоемкость, t — температура	c = Q / t	c(t)= Q’(t)
q — электрический заряд, I — сила тока, t — время	I=q / t	\I(t)=q’(t)

Примеры задач:

1. Нахождение пути, пройденного телом при прямолинейном движении.

Скорость движения материальной точки задается формулой Найти путь, пройденный точкой за первые 4 с от начала движения.

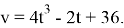
Решение:

= 256–16 + 144 = 384 м.

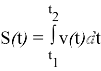
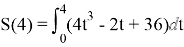
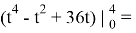
2. Вычисление работы силы, произведённой при прямолинейном движении тела.

Какую работу совершает сила в 10Н при растяжении пружина на 2 см?

Решение:

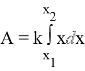
По закону Гука сила F, растягивающая пружину, пропорциональна растяжению пружины, т. е. F=kx. Используя условие, находим что k=10/0.02=500, F=500x. По формуле:

= 500

0,1

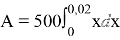
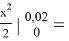
Литература:

1. Методика обучения физике в школе в школах СССР и ГДР, под ред. Зубова В. Г., Разумовского В. Г., Вюншмана М., Либерса К. — М., Просвещение, 1978.
2. Иванов А. И. О взаимосвязи школьных курсов физики и математики при изучении величин, — «Физика в школе», 1997, № 7, стр. 48.
3. Кожекина Т. В., Взаимосвязь обучения физике и математике в одиннадцатилетней школе, — «Физика в школе», 1987, № 5, стр. 65.