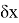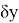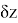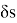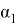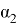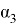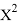Корреляционный анализ ошибок плановых и высотных координат



В данный момент встречаются много случаев несоответствия космических снимков и маршрутов транспортировки. Это потому, что мы ещё не пришли к единой системе координат, то есть существуют базы данных в разных системах координат, которые мы используем. Мы думаем, что использование разных систем координат дает небольшие ошибки. В данной статье пойдет речь об ошибках трансформации между системами координат, и приводится решение устойчивости этих ошибок с помощью математического анализа. В 2015 году швейцарский профессор Хуан Фан и доцент из КГУСТА им. Н. Исанова Акылбек Чымыров провели исследование, в котором доказали ошибки трансформации. Используя данные этих ошибок, я доказал устойчивость взаимосвязи между ними.

Ключевые слова: модель Гельмерта, коэффициент корреляции, ITRF-2005, KYRG-06, SK-63.

Введение

Координаты являются наиболее важной фундаментальной информацией в геопространственных базах данных. Координация системы должны быть определены и должным образом поддерживаться с помощью геодезических сетей. В противном случае, наборы данных, определенные в разных системах координат, могут быть несогласованными. Один простой пример — это более новые снимки Google Earth или на GIS. Эти спутниковые снимки относятся к ITRF-2005 и образуют новую кыргызскую геодезическую систему отсчета KYRG-06, глобальной геоцентрической системе координат, в то время как улицы и дороги определены в локальной системе триангуляции. Это вызвало несоответствие космических снимков и маршрутов транспортировки.

Кыргызстан восходит к советской эпохе. Кыргызская триангуляционная сеть состоит примерно из 9300 пунктов, разделенных на пункты 1-го порядка, 2-го порядка и 3-го порядка. Кыргызская триангуляция точки по существу являются частью советской сети триангуляции, которая определяет хорошо известную советскую систему координат Пулково 1942 г. или SK-42 на основе опорного эллипсоида Красовского. Поскольку SK-42 в основном используется в военных целях, создана гражданская версия SK-42 и названа как SK-63. Кыргызская нивелирная сеть включает около 7500 реперов, разделенных на 4 порядка. Он основан на системе высот уровня Балтийского моря 1977 года с нулевой точкой отсчета в Кронштадте.

Ожидается, что отныне все геодезические данные, базы данных ГИС и карты будут производиться в системе KYRG-06. Однако по историческим причинам все еще существует большое количество карт и базы данных в старой системе координат 1963 года (SK-63), карты прямоугольных координат SK-63 в проекции Гаусса-Крюгера, на основе параметров эллипсоида Красовского с зонами 3°. Эти координаты получаются, перемещая осевую зону меридианов и смещая начало координат и открывая для гражданского использования. А вот параметры трансформации между SK-42 и SK-63 засекречены в Кыргызстанe. Поэтому возникает необходимость переноса координат со старого SK-63 на новую систему KYRG-06. Такое преобразование можно осуществить разными способами, одним из которых является трехмерная трансформационная модель Гельмерта.

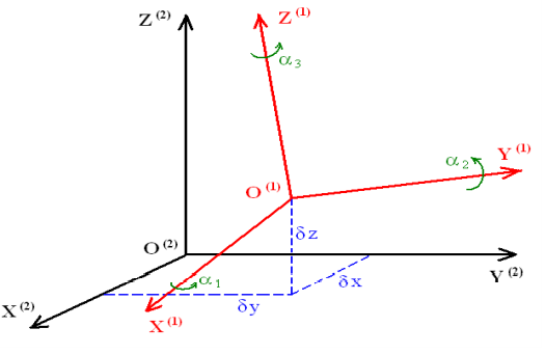
 3 перевода или сдвига

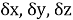
 1 изменение масштаба (коэффициент масштабирования)

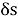
 3 угла поворота (угловая секунда)

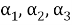
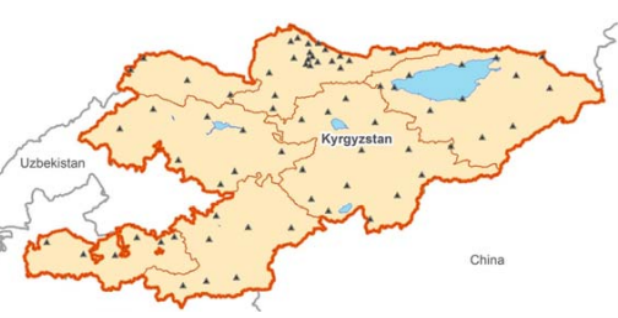
Основными массивами данных, использованными в данном исследовании, являются 70 кыргызских геодезических опорных пунктов по всей стране. На этих 70 станциях имеется:

1) Координаты картографической проекции (x; y), определенные в SK-63. Используя ссылку Красовского параметры эллипсоида

2) Нивелированные высоты в системе уровней Балтийского моря 1977 года. Пренебрегая высотой геоида, это дает нам приблизительную эллипсоидальную высоту на каждой контрольной станции.

3) Трехмерные координаты в ITRF2005 (KYRG-06), либо в виде прямоугольных координат (x; y; z) ITRF или геодезические координаты (φ; λ; h) ITRF. Теперь у нас есть два набора.

Ед. измер.	m	m	m	ppm	"	"	"
Параметры КР	-33, 951	-17, 705	-135, 11	-6, 082	-3, 779	-0, 698	2, 009
Параметры РФ	+23, 57	-140, 95	-79, 8	-0, 22	0, 00	-0, 35	-0, 79

Для сравнения также приводяится значения 7 параметров трансформации, оцененные из российских наборов данных (Комаровский, 2005). И результаты показали значительные ошибки в обоих случаях, и в параметрах Кыргызстана, и в России. Главной целью статьи является определение устойчивости взаимосвязи между этими явлениями, реагирует ли изменение одной на изменение другого. Для решения этих вопросов я использовал метод корреляции.

Метод корреляции.

В математической статистике взаимосвязь явлений и их признаков изучают методом корреляции. Под корреляцией понимают такую связь между случайными величинами, при которой одна случайная величина реагирует на изменения другой, вариациями своего условного математического ожидания. При обработке и использование статистических данных, необходимых для научных и практических выводов, важно проследить за изменением одного признака с изменением другого, т. е. нужно найти значения коэффициента корреляции. Задача корреляционного анализа состоит в том, чтобы выявить и установить связи между отдельными признаками, вытекающие из структуры объекта. При линейной зависимости корреляционное отношение называют коэффициентом корреляции и обозначают через Коэффициент корреляции может иметь значение в пределах

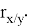
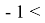
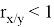
Величина коэффициента корреляции определяет устойчивость связи между случайными величинами; чем ближе значение к единице, тем теснее статистическая связь. Близкое к нулю значение коэффициента свидетельствует об отсутствии прямолинейной статистической связи

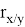
№	X	Y	Z	X*Y	X*Z	Y*Z
1	33, 55	17, 305	134, 71	580, 5828	4519, 521	2331, 157	1125, 603	299, 463	18146, 78
2	33, 65	17, 405	134, 81	585, 6783	4536, 357	2346, 368	1132, 323	302, 934	18173, 74
3	33, 75	17, 505	134, 91	590, 7938	4553, 213	2361, 6	1139, 063	306, 425	18200, 71
4	33, 85	17, 605	135, 01	595, 9293	4570, 089	2376, 851	1145, 823	309, 936	18227, 7
5	33, 951	17, 705	135, 11	601, 1025	4587, 12	2392, 123	1152, 67	313, 467	18254, 71
6	34, 051	17, 805	135, 21	606, 2781	4604, 036	2407, 414	1159, 471	317, 018	18281, 74
7	34, 151	17, 905	135, 31	611, 4737	4620, 972	2422, 726	1166, 291	320, 589	18308, 8
8	34, 251	18, 005	135, 41	616, 6893	4637, 928	2438, 057	1173, 131	324, 18	18335, 87
9	34, 351	18, 105	135, 51	621, 9249	4654, 904	2453, 409	1179, 991	327, 791	18362, 96
сумма	305, 555	159, 345	1215, 99	5410, 452	41284, 14	21529, 7	10374, 36	2821, 803	164293

*

*

*

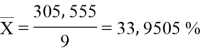
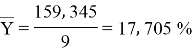
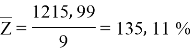
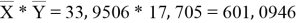
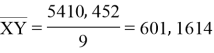
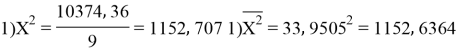
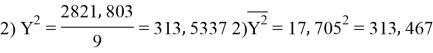
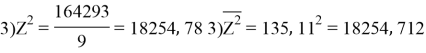
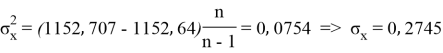
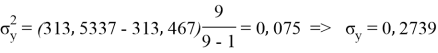
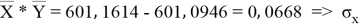
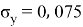
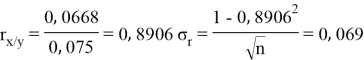
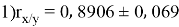
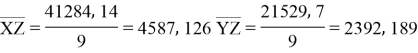
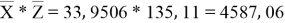
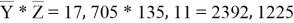
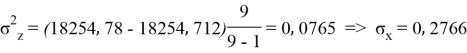
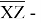
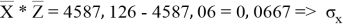
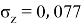
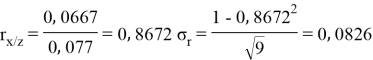
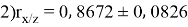
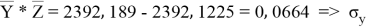
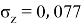
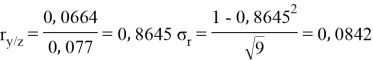
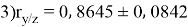
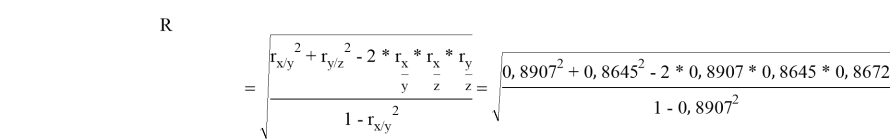
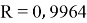
Заключение. В решении сначала мы находим 3 взаимосвязи между координатами. И они вышли в пределах допустимого. Из этих значений мы, используя формулу определения корреляции трёх признаков, т. е. совокупную корреляцию, находим значение 0,9964. Если коэффициент корреляции имеет значение в пределах от 0, 9 до ,1 не включая единицы, то корреляционная связь является весьма устойчивой.

Численные результаты показывают, что 7 параметров преобразования, оцененные по 70 кыргызским точкам, приводят к большим ошибкам. И результаты корреляционного анализа показали устойчивость этих явлений. Можно отметить, что смещение идет в западную часть. Необходимо для дальнейших исследований уменьшить ошибки преобразования. И прийти к единой системе координат, то есть необходимо перевести все карты и базы данных в новую систему координат.

Литература:

1. Рыжков П. А., Гудков В. М. Применение математической статистики при разведке недр. -Москва «Недра», 1966.
2. https://www. researchgate. net/publication/293707345_Coordinate_transformation_between_SK-63_and_ITRF_in_Kyrgyzstan, 2015.